Как отмечалось ранее, указанные выше системы являются нелинейными, то есть при приложении нагрузки зависимости между внешними силовыми факторами, внутренними усилиями и перемещениями не являются линейными, и их нахождение связано с определенными трудностями. Для расчета таких систем на практике применяются методы приращения внешней нагрузки (метод Эйлера), итеративные (метод Ньютона-Рафсона) и энергетические методы.
В этих случаях нагрузка, действующая на конструкцию, разбивается на ряд ступеней, на каждой из которых проводится линеаризация расчетов с учетом имевшегося ранее загружения, деформированного состояния и параметров матрицы жесткости.
200
Проиллюстрируем метод Ньютона-Рафсона на простом примере стержневых элементов (рис. 3.16).
Под действием силы Р в стержневой системе возникает перемещение w, первое приближение величины которого может быть определено из решения линейного уравнения
К1 · w1 = P
(3.72)
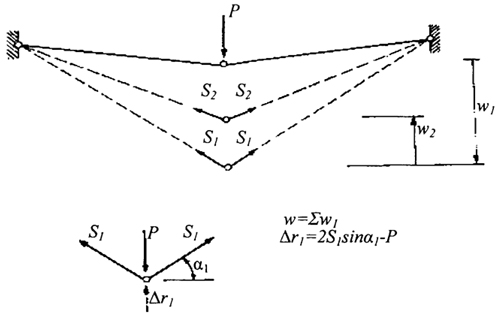Рис. 3.16. Иллюстрация итерационного процесса а - схема загружения; б - схема равновесия узла.
Зная величину перемещения, можно найти удлинения стержней и усилия в элементах S/. Указанные усилия и внешняя нагрузка не удовлетворяют условию равновесия узла (рис. 3.16, б) в деформированном положении. Такое равновесие возможно только для недеформированного состояния, поэтому для деформированной конструкции выделяют силы невязки, величина которых на первой ступени итерации
Δr1 = 3 · S1 · sin α1 - P
(3.73)
На втором шаге итерации, учитывая изменения геометрических параметров, полученные на первом шаге итерации, находят новое значение матрицы жесткости К2 и снова решают линейное уравнение
K2 · w2 = Δr1
(3.74)
откуда определяют перемещение w2.
Процесс итерации продолжается до тех пор, пока не будет выполнено требуемое условие точности расчета. Графическая интерпретация метода Ньютона-Рафсона иллюстрируется графиком рис. 3.17.
201
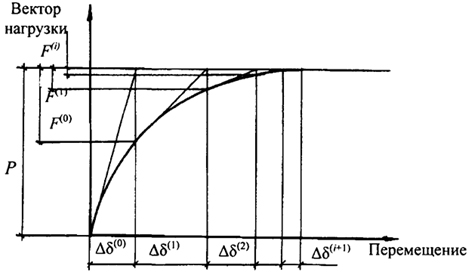Рис. 3.17. Графическая интерпретация метода Ньютона-Рафсона
Представленный здесь нелинейный итерационный процесс в сложных конструкциях (например, плоские вантовые сети) и при больших величинах внешней нагрузки может очень медленно сходиться, а в отдельных случаях вообще расходиться. Для ускорения сходимости итерационного процесса используется метод корректировки энергии деформации стержневой системы, включающий итерацию по Ньютону-Рафсону [84], [103], суть которого заключается в корректировке вектора перемещений d в процессе итерации путем введения скалярного параметра с:
d = c · d(k)
(3.75)
Метод корректировки энергии деформации иллюстрируется графиком (рис. 3.18).
Скалярный параметр с равен
c =
(3.76)
где А - работа внешних сил;
U - внутренняя энергия деформации.
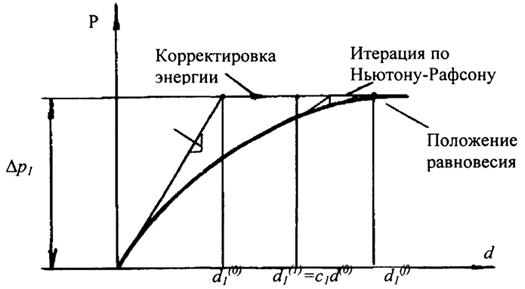Рис. 3.18. Корректировка энергии деформации при итерационном процессе
202
Он определяется из условия
Uk(0) + Uk(1) + Uk(2) = Ak
(3.77)
| где |
Uk(0) = · dT · Kk(0) · dk = · c2 · dk · Kk(0) · dk = c2 · Uk(0);
Uk(1) = · dkT · Kk(1) · dk = · c3 · dkT · Kk(1) · dk = c3 · Uk(1);
Uk(2) = · dkT · Kk(1) · dk = · c4 · dkT · Kk(2) · dk = c4 · Ur(2);
Ak = Ak-1 + pm · (c · dk - dk-1) = Ak-1 + c · pm · dk - pm · dk-1;
pm = . |
Параметр с является наименьшим положительным корнем уравнения.
c4 · Uk(2) + c3 · Uk(1) + c2 · U(0) - c · Bk,1 - (Ak-1 - Bk,2) = 0
(3.78)
| здесь |
Bk,1 = pm · k,
Bk,2 = pm · dk-1. |
Для первой ступени загружения (к = 1) уравнение (3.78) упрощается и преобразуется к виду
с3 · U1(2) + c2 · U1(1) + c · Ul(0) - В1,1 = 0.
(3.79)
при значениях
B1,1 =
;
B1,2 = 0; A0 = 0.
Усилия в стержнях узлов S на ступени загружения определяются по формуле
S = S(0)+ S(1)+ S(2) = (K(0) + · K(1) + · K(2)) · d
(3.80)
Здесь S(0), S(1), S(2) - соответственно линейная и нелинейные составляющие усилий.
Итерационный процесс продолжается до тех пор, пока величина невязки в уравнении равновесия внешних и внутренних сил не будет превышать требуемых условий точности расчета. И далее производится переход на следующую, более высокую ступень загружения, и итерационный цикл начинается вновь.
Завершение итерационного процесса происходит после достижения внешней нагрузкой расчетной величины, и невязка Δri, из условия равновесия усилий на последней ступени загружения не будет превышать принятых параметров точности расчета.
203
