Для гибких нитей с опорами, расположенными на разных уровнях (рис. 3.8) и загруженными вертикальной нагрузкой q(x), условие равновесия имеет вид
M - F · sin α · x + F · cos α · y = 0
(3.31)
184
Здесь М - балочный момент для пролета l.
Геометрические параметры нити показаны на рис. 3.8 и 3.9.
Из уравнения (3.31) получим
y = x · tg α -
(3.32)
Максимальная величина усилия в нити
FB = √(F · cos α)2 + (Rв + F · sin α)2
(3.33)
Длина нити в конечном состоянии может быть получена из выражения (3.23), где величина y` определяется из уравнения (3.32)
y` = tgα - · = tgα -
(3.34)
где Q - величина поперечной силы возникающей в балке, пролетом l, загруженной нагрузкой q(x).
Подставляя (3.34) в (3.23), получим
L = √1 + (tg α - )2dx
(3.35)
Рис. 3.8. Гибкая нить с опорами на разных уровнях
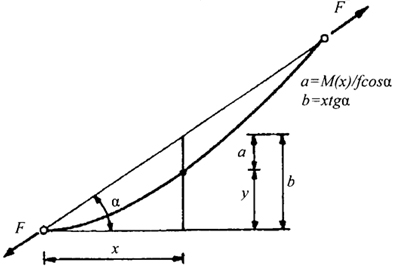Рис. 3.9. Координаты нитей
185
Упругое удлинение нити составит:
ΔL = · [1 + (tg α - )2]dx
(3.36)
Уравнение (3.7) с учетом выражений (3.35) и (3.36) имеет вид:
√1 + (tg α - )2 dx = L0 · (1 + αt · Δt) + · [1 + (tg α - )2]dx
(3.37)
Уравнение (3.37) применимо при любых видах вертикальной нагрузки q(x) и любых значениях стрелок провисания нитей. Оно точно отражает поведение нити под нагрузкой. Однако применение такого уравнения в практике расчетов вызывает затруднения в связи со сложностями численных итеративных вычислений. Для упрощения практических вычислений используются приближенные решения, в основу которых положена формула, предложенная В.К. Качуриным [19], для определения длины нити:
L = ls + Q2 · dx
(3.38)
где ls - хорда нити (рис. 3.8).
Упругие деформации нити могут быть представлены в следующем виде:
ΔL =
(3.39)
Подставляя (3.38), (3.39) в уравнение (3.7), получим
ls + · Q2 · dx = L0 · (1 + α · Δt) +
(3.40)
после преобразования будем иметь
F3 + F2 · E · A ·[1 - · (ls - αt · Δt · L0)] = Q2 · dx
(3.41)
Если угол наклона хорды к горизонту равен нулю, то выражение (3.41) преобразуется к виду (3.29). При q(x)=q=const уравнение (3.41) имеет вид
F3 + F2 · E · A ·[1 - · (ls - αt · Δt · L0)] = | E · A · cos α · q2 · l3 |
| 24 · L0 |
(3.42)
Если внешняя нагрузка действует в горизонтальном направлении (то есть q=q(y), (рис. 3.10)), то выражение (3.41) принимает следующую форму:
F3 + F2 · E · A ·[1 - · (ls - αt · Δt · L0)] =
(3.43)
186
то есть горизонтальную нагрузку можно рассматривать так же, как и вертикальное загружение, только с заменой пролета l на величину h - высоту подъема верхней опоры нити (рис. 3.10).
Сравнение расчетов по приближенной (3.41) и точной (3.37) формулам для равномерной нагрузки показало [104]:
- При малых значениях а тяжение F нити, направленное по хорде, полученное по формуле (3.41), несколько выше значений, полученных по формуле (3.37). При больших значениях угла а эти соотношения меняются наоборот.
- Различие между двумя решениями зависит не только от угла наклона хорды к горизонту, но и от величины относительной стрелки провисания нити cos α · f/l. Если отношение cos α ·f/ls меньше 0,05, то разница между расчетными величинами может считаться пренебрежимо малой. Величина относительной стрелки провисания cos α · f/ls на практике зависит от угла наклона хорды ls нити. Чем больше угол наклона, тем меньше отношение cos α · f/ls. Для оттяжек конструкций такое отношение колеблется в пределах 0.02 ÷ 0.05. Соотношения, полученные выше, имеют место и при других видах загружения. Формула (3.41) может быть использована для практических расчетов.
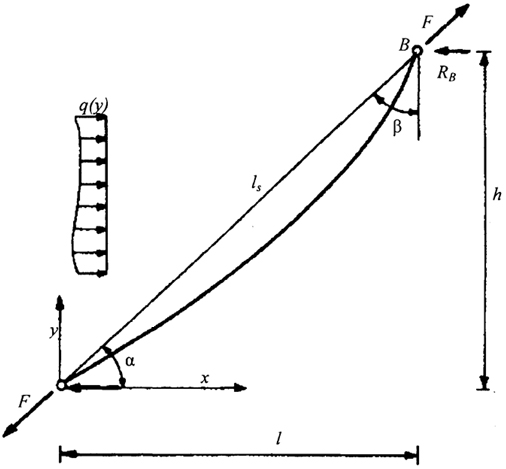Рис. 3.10. Нити с горизонтальным приложением нагрузки
187
