Гибкая нить может являться самостоятельным отдельным несущим элементом конструкций покрытия, элементом тросовых ферм, а также частью пространственных плоских и объемных систем.
Гибкой называют нить, практически лишенную изгибной жесткости. Форма ее провисания зависит от формы нагрузки, места ее приложения, направления, условий закрепления на опорах.
Ординаты у(х) нити в направлении действующей нагрузки g(x) определяются уравнением
у(х)= ·M(х)
(3.1)
где у(х) - провес нити в сечении х;
М(х) - балочный изгибающий момент (рис. 3.1) в сечении х от нагрузки g(x);
Н - распор, горизонтальная составляющая растягивающего нить усилия.
Представленная форма нити отражена эпюрой моментов фиктивной балки (рис. 3.1, а, б), загруженной нагрузкой g(x).
Рис. 3.1. Гибкая нить под действием поперечной нагрузки:
а - форма загруженной нити; б - фиктивная балка и эпюра изгибающих моментов от действия поперечной нагрузки g(x)
Пропорциональное увеличение нагрузки по отношению к начальной для нитей конечной жесткости ЕА вызывает появление дополнительных упругих деформаций Δf для середины пролета со (рис 3.2, а).
Асимметричное дополнительное загружение вызывает появление наряду с упругими деформациями кинематических перемещений ωi (рис. 3.2, б).
170
Рис. 3.2. Изменение геометрии гибкой нити под действием различных загруже-ний: а - упругие деформации под действием пропорционального увеличения нагрузки; б - дополнительные кинематические перемещения от действия асимметричного загружения; в - гибкая нить и фиктивная балка при различных видах загружения
Рассмотрим гибкую нить, загруженную постоянной нагрузкой g, которая равномерно распределена по площади покрытия. Вертикальная составляющая проекции такой нагрузки на горизонтальную плоскость (рис. 3.3) распределяется согласно уравнению
q(x) =
(3.2)
В этом случае нить принимает очертание цепной линии по уравнению [19]
у = m · (ch - 1)
(3.3)
где т =
.
В строительной практике часто принимается, что нагрузка от собственного веса будет равномерно распределенной по горизонтали q(x) - g = const.
В этом случае нить принимает очертание квадратной параболы.
y =4 · · (l - x) · x
(3.4)
Длина гибкой нити определяется из выражения
L = √1+ y 2 · dx
(3.5)
при у = -
·
(2 · x - l) .
171
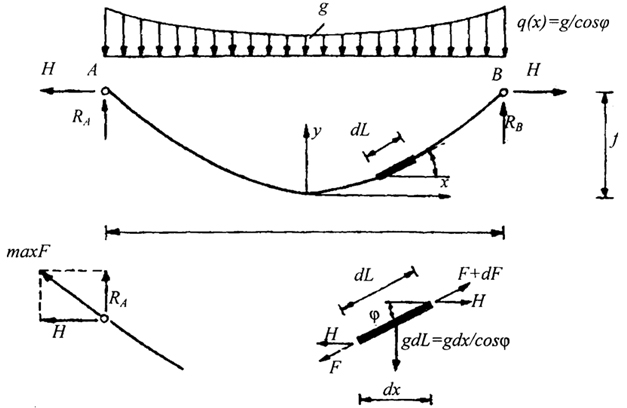Рис. 3.3. Гибкая нить под действием нагрузки собственного веса
После интегрирования выражения (3.5) длина нити в форме параболы
L = l · [1 + · - · ± …]
(3.6)
На практике в уравнении (3.6) при определении длины нити ограничиваются двумя первыми членами. Длина нити в начальном и конечном состоянии может быть представлена в виде
L = L0 + ΔL + ΔLt
(3.7)
где L - длина нити в конечном состоянии после приложения нагрузки,
L0 - длина нити в начальном состоянии (при g = 0),
ΔL -упругое удлинение нити под действием внешней нагрузки,
ΔLt - удлинение нити от воздействия температуры.
Принимая во внимание, что
f =
(3.8)
Получим
L ≈ l · (1 + )
(3.9)
Упругие деформации нити
ΔL ≈
(3.10)
Подставляя (3.9), (3.10) в (3.7), получим
172
l · (1 + ) = L0 · (1 + αt · Δt) +
(3.11)
После преобразования (3.11) получает вид
H3 + H2 · E · A · [1 - · (l - αt · Δt · L0)] =
(3.12)
Вышеуказанные уравнения получены для гибкой нити в форме параболы, отличающейся от действительной кривой в форме цепной линии.
Для цепной линии стрелка провисания fц и распор Нц больше соответствующих значений для параболы fп и Нп и с увеличением
отношения - эта разница увеличивается.
На рис. 3.4 показаны формы цепной линии и параболы.
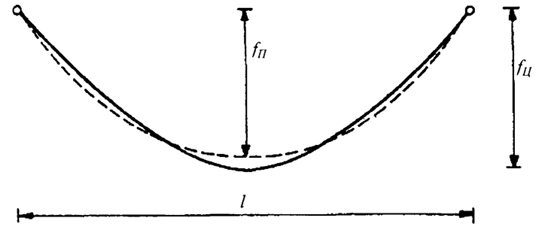Рис. 3.4. Гибкая нить в форме цепной линии и параболы
Однако при значениях f/l ≤ 0,25 различия между расчетными величинами, полученными по формулам для различных кривых, пренебрежимо малы и для пологих нитей [f/l = (
÷
)
] в качестве расчетной кривой может быть принята парабола.
При любых значениях вертикальной нагрузки, действующей на нить конечной жесткости ЕА, с расстоянием между опорами, равным l, условие равновесия в каждой точке запишется в виде
М - Н · у = 0
(3.13)
Откуда
y =
(3.14)
Величина стрелки провисания, расположенной в точке нахождения максимального момента
f =
(3.15)
173
или
H =
(3.16)
Формула (3.16) для определения величины распора имеет ограниченную область применения, так как очертание кривой гибкой линии и ее стрелка провисания заранее, как правило, не известны.
Длина нити, как отмечалось ранее, равна
L = √1 + y 2 · dx
(3.17)
Первая производная по координате у имеет вид
y = · =
(3.18)
Здесь Q поперечная сила от действия равномерно распределенной нагрузки q(x), определяемая как для балки пролетом l, расположенной на двух опорах.
Подставляя (3.18) в (3.17), будем иметь
L = √1 + · dx
(3.19)
Упругие деформации нити, [104]
ΔL = · (1 + ) · dx
(3.20)
Решая совместно уравнения (3.7), (3.19), (3.20), получим
√1 + ) · dx = L0 · (1 + αt · Δt) + · (1 + ) · dx
(3.21)
Здесь αt - коэффициент линейного расширения (для стальных канатов αt = 0,000012),
Δt - изменение температуры.
Уравнение (3.21) справедливо для любых значений g(x) и любых значений стрелок провисания. Однако его решение может быть выполнено только методом численной итерации.
Если разложить выражение (3.5) в ряд Тейлора, то получим
L = (1 + · y2 - · y4 + · y6 - …) · dx
(3.22)
В выражении (3.22) слагаемые, кроме первых двух, пренебрежимо малы, отбросим их, тогда
L = (1 + · y2) · dx
(3.23)
Подставляем (3.18) в (3.23)]
174
L = (1 + · ) · dx = l + Q2 · dx
(3.24)
Формулы для определения интеграла ∫ Q2 · dx приведены в таблице 3.1
Решая совместно (3.24), (3.10), (3.7), получим
l + · Q2 · dx = L0 · (1+ αt · Δt) +
(3.25)
После преобразования (3.25) будем иметь
H3 +H2 · E · A · [ 1 - · (l - αt · Δt · L0)] = · Q2 · dx
(3.26)
При q(x)=q=const поперечная сила Q
Q = - q · x
(3.27)
Тогда
· ( - q · x)2 · dx =
(3.28)
Уравнение (3.26) с учетом (3.28) имеет вид
H3 + H2 · E · A · [ 1 - · (l - αt · Δt · L0)] =
(3.29)
Уравнения (3.12) и (3.29) идентичны.
Таблица 3.1
Формулы для определения интеграла
Q2dx
| № |
Схема нагружения |
Q2dx |
| 1 |
 |
|
| 2 |
 |
|
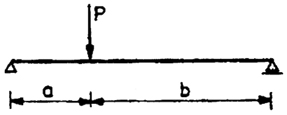175
Продолжение таблицы 3.1
| № |
Схема нагружения |
Q2dx |
| 3 |
 |
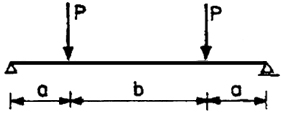2P2a |
| 4 |
 |
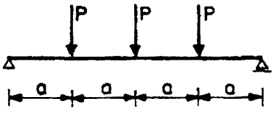5P2a |
| 5 |
 |
|
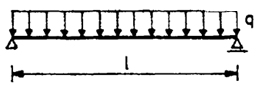| 6 |
 |
+ + |
| 7 |
 |
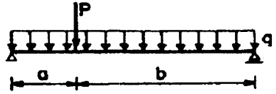+ + Pqab |
| 8 |
 |
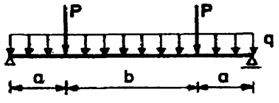+ 2P2a + 2Pqa(l - a) |
176
| 9 |
 |
|
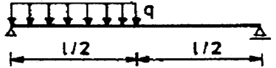| 10 |
 |
|
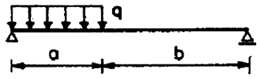| 11 |
 |
+ l3 +
+ q1l3 |
| 12 |
 |
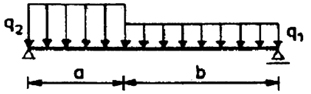+ a3 (4l - 3a) + (q2 - q1) q1a2 (l/2 - a/3) |
| 13 |
 |
|
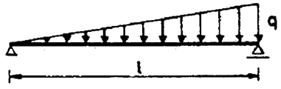| 14 |
 |
+ + (1 - a2/l2) |
| 15 |
 |
+ + |
| 16 |
 |
+ + + + 2q1Pab (1/2 - a/3l - b/6l) + 2q2Pab (1/2 - b/3l - a/3l) |
| 17 |
 |
|
177
Продолжение таблицы 3.1
| № |
Схема нагружения |
Q2dx |
| 18 |
 |
|
| 19 |
 |
|
| 20 |
 |
|
| 21 |
 |
|
| 22 |
 |
|
* - парабола третьего порядка
Как показывает анализ, в результатах расчета гибких нитей по формулам (3.21) и (3.29) при различных их геометрических параметрах имеются следующие отличия:
- При расчете по приближенной формуле (3.29) получаются большие значения распора Я по сравнению со значениями, вычисленными по формуле (3.21). Для пологих нитей при ≤ 0,1 ÷ 0,15 такие различия пренебрежимо малы. В то же время для таких нитей изменения температуры оказывают большее влияние, причем уменьшение температуры вызывает большее изменение распора, чем соответствующее увеличение температуры.
- Учет упругих деформаций позволяет точнее определить величину распора, значение которого для нерастяжимых нитей (то есть без учета упругих деформаций) больше, чем для деформируемых. При больших стрелках провисания (при f/l ≥ 0,25) влиянием деформируемости нитей и температурных напряжений можно пренебречь.
178
Наряду с упругими деформациями и температурными воздействиями на работу гибких нитей оказывают большое влияние деформации опорных узлов. Виды деформаций приведены на рис. 3.5.
Вертикальные перемещения (рис. 3.5, а) опорных узлов не вызывают каких-либо изменений напряженного состояния отдельно стоящих гибких нитей. Если нить является составляющей перекрестной системы (то есть взаимодействует с другими нитями), то вертикальные перемещения вызывают изменения усилий взаимодействия в других нитях, а следовательно, и изменения величины внешних воздействий на рассматриваемую нить.
Горизонтальные перемещения (рис. 3.5, б) приводят к изменению величины пролета нити и к соответствующим изменениям величины распора.
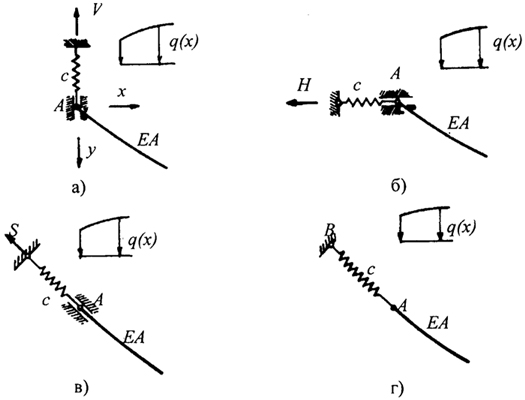Рис. 3.5. Виды перемещений опор гибких нитей: а - только вертикальные перемещения; б - только горизонтальные перемещения; в - перемещения по касательной к кривой нити в точке опирания; г - общий вид опорных перемещений
Приращение распора зависит от геометрических параметров, жесткостных характеристик, вида загружения и величины опорного смещения нити. Величина опорного смещения нити чаще всего пропорциональна величине распора и его определение производится методом итерации по формуле
H3 + H2 · e · A · [1 - · (l - Δl)] = · Q2 · dx
(3.30)
179
Здесь Δl - величина горизонтального перемещения опор.
Алгоритм определения величины распора может быть проиллюстрирован следующим образом:
- В исходном состоянии рассматриваем гибкую нить с фиксированными геометрическими параметрами и значениями жесткостных характеристик как загруженную внешней нагрузкой и не имеющую горизонтального смещения опор (рис. 3.6). Определяем величину распора.
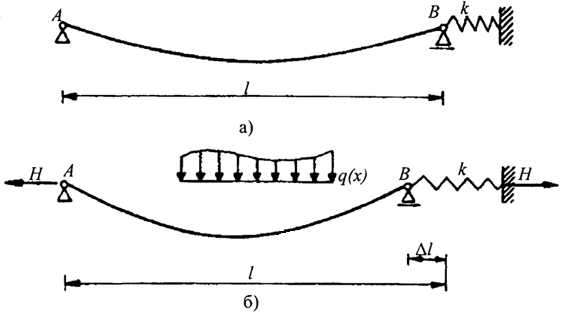Рис. 3.6. Гибкая нить со смещаемой опорой а - исходное состояние; б - работа под нагрузкой
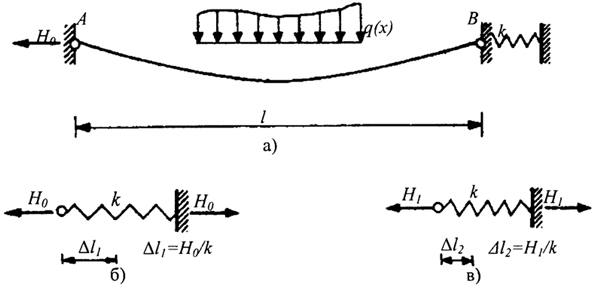Рис. 3.7. К расчету гибкой нити с учетом горизонтального смещения: а - исходное состояние; б - первое приближение; в - второе приближение
- Допускаем горизонтальную податливость опоры В, причем величина горизонтального смещения Δl (рис. 3.7) пропорциональна начальной величине распора Н0. По уравнению (3.30) находим новое скорректированное значение распора H1, величина которого будет меньше исходного значения.
- По полученному значению Н1, находим новое скорректированное значение горизонтального смещения Δl2, а используя его и новую величину распора Н2 Итерационный процесс прекращается тогда, когда разность между последующими значениями распора не превышает предельно допустимой величины погрешности расчета.
180
Величины перемещений опорных узлов под углом (рис. 3.5, в, г) могут быть разложены на горизонтальную и вертикальную составляющие, влияние каждой из них на напряженное состояние нити аналогично изложенному выше.
Пример 1
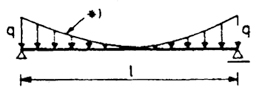
Определить величину распора в нити (см. рис.), загруженной равномерно распределенной нагрузкой q = ЗкН/м, при ЕА = 1 ООООО кН и L0 = 71 м.
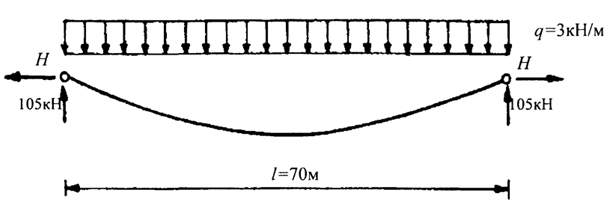Рис. Нить, загруженная равномерно распределенной нагрузкой
Уравнение (3.12) может быть представлено в виде
H3+ в - H2 - с = 0,
(а)
Если в первом приближении принять ЕА -∞, то значение распора
H = H1 = √| Q2 · dx |
2 · (L0 · (1 + αt · Δt) - l)
|
(б)
или при q = const
H = H1 = q · l ·√| l |
| 24 · (L0 · (1 + αt · Δt) - l) |
(в)
Используя метод Ньютона, выражение для распора Н3 будет иметь вид [58]:
Hi = | 2 · Hi-13 + b · Hi-l2 + c |
| 3 · Hi-12 + 2 · b · Hi-l |
(г)
Подставим значения в формулу (в), получим
H = 3 · 70 · √ = 358,6kN
Коэффициенты в и с в формуле (в)
181
в = 100000 · (1 -
) = 1408,45 71
c =
= 18,11 · 10
7
24-71 Второе приближение по формуле (г) равно
H2 =
| 2 · 358,63 + 1408,45 · 358,62 + 18,11 · 107 |
| 3 · 358,62 + 2 · 358,6 · 1408,45 |
.
Следующее приближение составит:
H3 = 323,4kN, H4 = 323,4kN → H = 323,4kN .
Если принять первое приближение значения распора относительно большой величиной, например Н1 = 1000кН, то получим следующий ряд приближений:
Н2 = 617,1, H3= 412,2, H4 = 335,4, H5= 323,6, H6 = 323,4
Из этого следует, что формула (г) позволяет очень быстро получить искомый корень даже в тех случаях, когда разница между первым приближением и искомым значением весьма значительна. Поэтому в качестве первого приближения вместо значений, полученных по формуле (б), можно принимать H1 = А · Rk (где Rk - расчетное сопротивление каната).
Пример 2
Гибкая нить (рис.) пролетом l = 40 м и исходной длиной L0 = 40,5 м загружена начальной нагрузкой q0 = 0.5кН/м, а затем нагрузкой Δq = 2кН/М. Определить величины распора Н0 , ΔH, если жесткость нити равна ЕА = 50000кН.
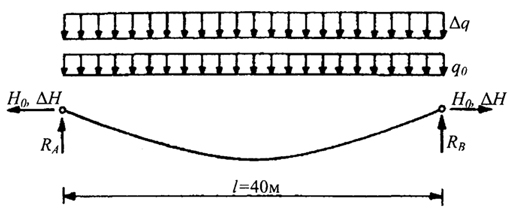Рис. Гибкая нить под действием нагрузок q0 и Δq
1. Определяем величину распора Н0. Из уравнения (3.12) получим
H30 + H20 · 50000 · (1 -
) =
| 50000 · 0,52 · 403 |
| 24 · 40,5 |
,
H30 + 617,28 ·H20 = 823045,3
откуда H0 = 35,5кН.
182
2. Определяем величину ΔH. Нагрузка, действующая на нить, равна:
q = q0 + Δq - 0,5 + 2,0 = 2,5kN/т. Из уравнения (3.12) получим
H3 + H2 · 50000 · (1 -
) =
| 50000 · 2,52 · 403 |
| 24 · 40,5 |
,
H3 + 617,28 · H2 = 20576131,7
Решением уравнения будет:
Н = 162,4kN
ΔH = Y - Y0 = 162,4 - 35,5 = 126,9kN
Пример 3
Определить величину распора f гибкой нити пролетом l = 50 м (см. рис.), загруженной равномерно распределенной нагрузкой q = 0,2кН/м при изменении температуры в ней Δt от -50°С до +50°С. Жесткость нити EA = 100000кН, ее начальная длина L0 = 0,5 м, коэффициент температурного расширения αt, = 0,000012 1/град.
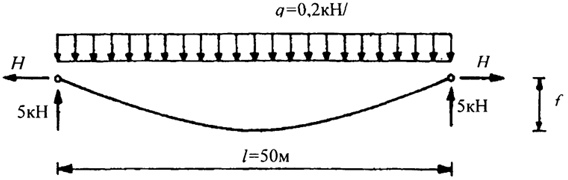Рис. Гибкая нить, загруженная равномерно распределенной и температурной нагрузками
Запишем выражение для определения величины распора при Δt = -50°С по формуле (3.14):
H3 + H2 · 100000 · (1 -
·
(50 - 0,000012 ·
(-50
) · 50,5
) =
| 100000 · 0,22 · 503 |
| 24 · 50,5 |
,
H3 + 930,1 · H2 = 412541,25
Решим уравнение, получим H = 20,8кН. При остальных значениях Δt, принимаемых с шагом 20°С, будем иметь
Δt = -30°С H = 20,5; Δt = -10°С H = 20,3;
Δt = 0°С H= 20,1; Δt = 10°С H = 19,9;
Δt = 30°С H = 19,7;Δt = 50°С H= 19,5.
Как видно из расчетов, уменьшение температуры вызывает большее изменение распора, чем увеличение. И если производить подобные расчеты для нитей с другими стрелками провеса, то будет выявлено, что нити с малым отношением f/l более чувствительны к температурным воздействиям.
183
Пример 4
Определить величину распора гибкой нити пролетом l = 50 м (рис.), загруженной равномерно распределенной нагрузкой q = 0,2кН/м при смещении опоры Δt от -7,5 см до +7,5 см. Остальные исходные данные аналогичны примеру 3.
1. Запишем уравнение для определения распора, используя формулу (3.15), при Δt = 0.
H3 +H2 · E · A · (1 -
) =
.
2. Подставим в уравнение величину смещения Δt = -7,5 см, получим
H3 + H2 · E · A · (1 - 50 -
) =
| 100000 · 0,22 · 503 |
| 24 · 50,5 |
H3 + 1138,6 · H2 = 412541,25
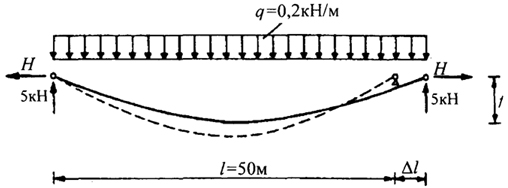Рис. Гибкая нить, имеющая смещение под нагрузкой опорного узла
Решение уравнения дает H = 19,0 кН. При остальных значениях Δl получим
Δl = -5,0 H = 19,3; Δl = -2,5 H 19,7;
Δl = 0 H = 20,1; Δl = 2,5 H = 20,6;
Δl = 5,0 H = 21,2; Δl = 7,5 Н= 21,8.
Как видно из расчетов, позитивные смещения опоры оказывают влияние аналогичное уменьшению температуры, и такое влияние больше для нитей с малыми стрелками провисания.
184
