Для висячих конструкций покрытия характерным является наличие основного несущего конструктивного элемента, работающего на растяжение. В качестве такого элемента могут использоваться как гибкие профили из высокопрочной стали - канаты, тросы, стержни, листы, так и изгибно-жесткие элементы из прокатных профилей или стержневых конструкций.
Висячие покрытия зданий и сооружений представляют собой пространственные системы, образованные пролетными несущими и ограждающими конструкциями, воспринимающими внешние нагрузки, и опорными конструкциями, работающими во взаимодействии с пролетными. Такие системы являются распорными. Для восприятия распора (горизонтальной составляющей тяжения тросов или оболочки) предназначена опорная конструкция. Стоимость опорной конструкции может составлять значительную часть всего покрытия. Удачность выбора конструктивной формы здания, а следовательно, и покрытия в значительной мере определяет затраты на его возведение.
Вопросам проектирования висячих конструкций зданий и сооружений посвящен целый ряд работ отечественных и зарубежных авторов [16],[58], [59]-[63],[66],[73] и другие.
Висячие конструкции покрытия имеют целый ряд преимуществ -это легкость, разнообразие архитектурных форм, хорошая сейсмостойкость. Вместе с тем такая конструкция имеет и ряд недостатков: повышенная деформативность, трудности водоотвода с покрытия, специфические особенности изготовления и монтажа и другие.
Висячие конструкции нашли применение в практике строительства нашей страны, в то же время в силу специфики использования каната как конструктивного элемента, повышенных требований к квалификации изготовителей, необходимости применения специальных инструментов и оснастки все это не привело к массовому применению в строительстве. Архитектурная выразительность зданий и сооружений с применением висячих систем, легкость и изящество конструктивных форм заслуженно снискали популярность использования таких систем в странах Западной Европы и Америки.
Канат в висячих конструкциях, имея изгибную жесткость, равную нулю, воспринимает только растягивающие усилия. Его продольная ось при действии внешней нагрузки (рис. 2.27,а) искривлена, только тогда он может работать при вертикальном поперечном загружении (рис. 2.27, б, в).
Напряжение в сечении каната от действия продольной силы, в отличие от напряженного состояния изгибно-жестких элементов (рис. 2.28), равномерно и позволяет более экономично использовать прочностные свойства материала. Это является одной из причин легкости висячих систем и возможности перекрытия ими больших пролетов.
92
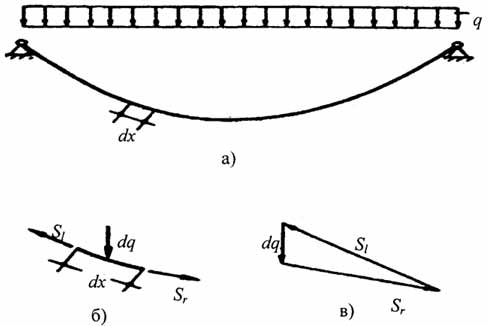Рис. 2.27. Работа каната при действии равномерно распределенной нагрузки: а - общий вид загруженного каната; б - бесконечно малый элемент под нагрузкой; в - треугольник сил
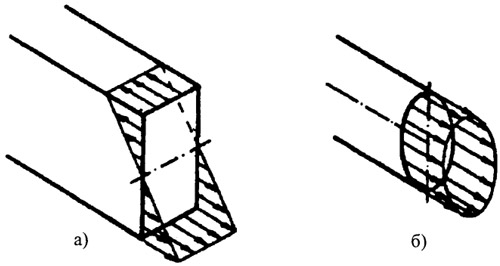Рис. 2.28. Сравнение эпюр изгибных (а) и растягивающих (б) напряжений
Характеристикой плоской кривой или искривленной поверхности является кривизна к, которая для любой точки М равна обратной величине радиуса в этой же точке к = 1/R (рис. 2.29.а). Для криволинейной поверхности в точке М может быть проведено бесчисленное множество радиусов, однако в этом множестве существует радиус R1, величина которого максимальна и R2 - величина его минимальна. Плоскости расположения радиусов повернуты на 90° друг к другу (рис. 2.29, б).
Эти параметры кривизны считаются главными и обозначаются как К1 и К2 (рис. 2.29, б).
93
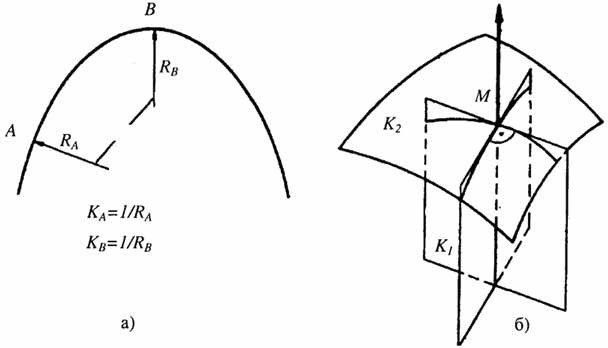Рис. 2.29. Изображение кривизны поверхности: а - кривая на плоскости; б -криволинейная поверхность
Гауссова кривизна определяется из выражения
к = · или k = ·
и служит для классификации поверхностей. Если оба радиуса находятся с одной стороны поверхности (оба радиуса или положительны, или отрицательны, к>0), пятно касания к поверхности эллиптическое (рис. 2,30. а), если R1 = R2, то поверхность шаровая. Если знаки радиусов R1 и R2 различны (к<0), то есть они расположены с разных сторон поверхности, окрестность точки М расположена на гиперболической седловидной поверхности (рис. 2,30. в).
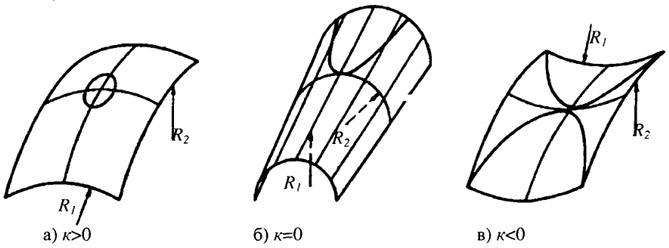Рис. 2.30. Поверхности гауссовой кривизны: а - положительной к > 0; б - нулевой к = 0; в - отрицательной к < О
Если один из радиусов кривизны равен бесконечности (к = 0), то поверхность цилиндрическая или конусообразная, пятно касания параболическое (рис. 2.30, б).
94
Средняя кривизна характеризуется параметром H =
·(
+
). При Н = 0, то есть
R1 = -R2, получается поверхность минимальной площади и минимального объема. Это свойство учитывается при формировании опорного контура.
Поверхности гауссовой кривизны могут быть использованы при проектировании пространственных конструкций. Висячие и тентовые конструкции чаще всего являются поверхностями отрицательной гауссовой кривизны (к < 0). Пневматические конструкции и решетчатые оболочки, напротив, являются поверхностями положительной гауссовой кривизны.
Классификация висячих конструкций весьма разнообразна. Они отличаются по условиям стабилизации (однопоясные и двухпоясные), способам соединения несущих и стабилизирующих вант (двухпоясные системы и тросовые фермы), характером работы системы (плоские, пространственные), включением в систему изгибножестких элементов (комбинированные или гибридные конструкции), жесткие нити и другие. Рассмотрим некоторые из них.
95
