В отличие от известной конструкции предварительно напряжённого стержня [2], наряду с расширением области упругой работы материала в предлагаемом решении стержня возможно дополнительно провести перераспределение усилий между элементами, что позволяет не только повысить эффективность применения высокопрочной стали и дополнительно снизить массу стержня, но и при включении его в статически неопределимую систему дополнительно провести благоприятным образом перераспределение усилий между другими элементами стержневой конструкции.
Стержень включает в себя "жёсткий" элемент 1 (рис. 2.5, 2.6), предел текучести материала которого равен σT1, гибкий элемент 2, с пределом текучести σT2 =(3 - 10) · σT1, анкер 3, фиксирующие прокладки 4, концевые обоймы 5. Внешняя нагрузка прикладывается к анкерам гибкого элемента 2, которые имеют выступающие буртики.
72
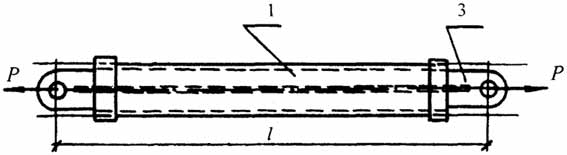Рис.2.5. Предварительно напряженный стержень
После создания предварительного напряжения между буртиками анкеров и концевых обойм имеется зазор f, называемый конструктивным.
В отличие от известного решения [2], работа такого предварительно напряжённого стержня после создания предварительного напряжения разбивается на три этапа. На первом, в пределах усилия предварительного напряжения (рис. 2.7), работают совместно гибкий 2, и "жёсткий" 3 элементы. На втором, после исчерпания усилия предварительного напряжения, "жёсткий" элемент выключается из работы и вся нагрузка воспринимается высокопрочным гибким элементом 2. На третьем, после замыкания конструктивного зазора (, совместно работают до исчерпания несущей способности каждого из материалов элементы 1 и 2. Если вместо фиксирующих прокладок 4 между анкером 3 и "жёстким" элементом 1 поставить пружину (рис. 2.8), то диаграмма работы стержня под действием внешней нагрузки имеет другой вид (рис. 2.9) и её характер зависит от величины конструктивного зазора и жесткостных характеристик пружины.
Используя уравнения равновесия и совместности деформаций при работе в стадии предварительного напряжения и действия внешней нагрузки, получим следующие зависимости для стержня (рис. 2.5, 2.6):
X = σ01 · A1 = σ02 · A2
(2.13)
P = (σ01 + R1) · A1 + (R2 - σ02) · A2 = (σ01 + R1) · A1 + X1
(2.14)
P = R1 · A1 + R2 · A2
(2.15)
X = | A2 · m · (P + A1 εf · E1 |
| A1 + A2 · m |
(2.16)
Δl1 = = | (R1 - σ02 - εf · E2) · l |
| E2 |
(2.17)
где σ01 - величина расчётного предварительного напряжения в "жёстком" элементе;
σ02 - величина предварительного напряжения в гибком элементе;
R1, R2 - расчётные сопротивления в "жёстком" и высокопрочном гибком элементах;
X1 - приращение усилия в гибком элементе от действия внешней нагрузки;
l - длина предварительно напряжённого стержня;
Х - величина усилия предварительного напряжения;
Δl1 - удлинение стержня от нагрузки.
73
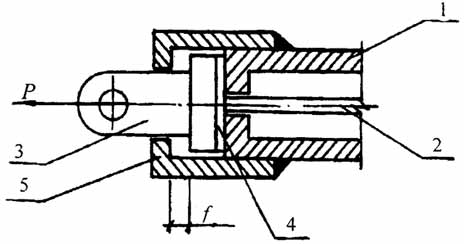Рис.2.6. Анкерный узел:
1 - жесткий элемент; 2 - гибкий элемент; 3 - анкер; 4 - фиксирующая прокладка; 5 - концевая обойма
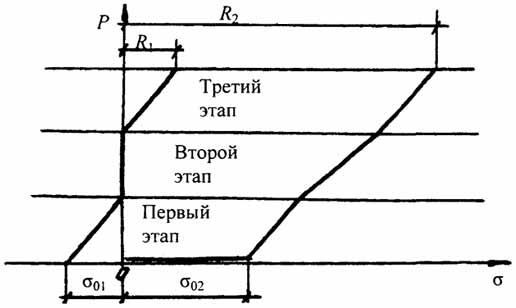Рис.2.7. Диаграмма работы предварительно напряженного стержня
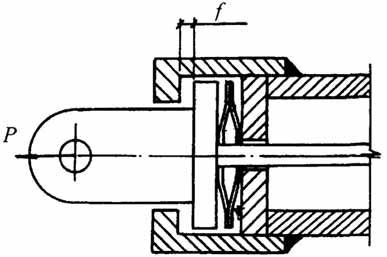Рис.2.8. Анкерный узел с пружиной
74
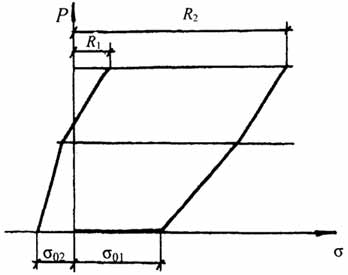Рис.2.9. Диаграмма работы предварительно напряженного стержня с пружиной
В формулах (2.13 - 2.17) представлены абсолютные значения напряжений без учёта знака.
Решая совместно уравнения (2.12 - 2.17), получим формулы для определения требуемой площади сечения "жёсткого" и гибкого элементов стержня
A1 = | P[k1 - m · ( + 1 + α)] |
| [( + 1) (k1 · α] · R1 |
(2.18)
A2 = = | P |
| [( + 1) (k1 - m) - m α] · R1 |
(2.19)
где
Выражения (2.17) и (2.18) можно представить в виде:
= | k1 - m · ( + 1 + α) |
| [( + 1) (k1 - m) - m · α] · R1 |
(2.20)
= |
| [( + 1) (k1 - m) - m · α] · R1 |
(2.21)
На рис. 2.10 представлено графическое отображение зависимости параметров A1/Р и А2/Р в функции от параметров σ01 /R1,k1,α, т.
75
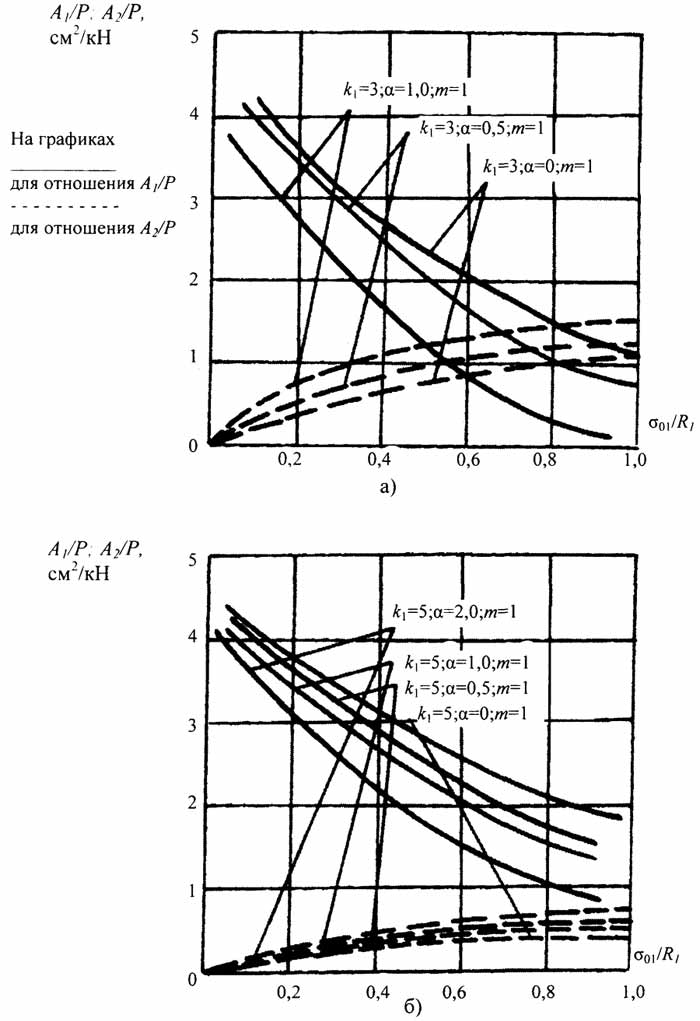Рис.2.10. Зависимость параметров ;
от величины при фиксированных значениях k1; α; m.
76
Влияние величины конструктивного зазора характеризуется параметром α, при α = 0 конструктивный зазор отсутствует, что эквивалентно работе традиционно известного предварительно напряжённого стержня.
На рис. 2.11 - 2.12 представлены графики, отражающие изменение величины суммарной площади сечения предварительно напряжённого стержня, отнесённой к единице силы в функции параметров σ01/R1 и к1.
Как видно из рис. 2.11 - 2.12, площадь сечения и масса предварительно напряжённого стержня без конструктивного зазора не зависит от соотношения прочностных характеристик материалов. Максимальное снижение массы не превышает 50% от массы обычного стержня, работающего на растяжение. Если принять величину конструктивного зазора, равной нулю (α = 0), то зависимости (2.18 - 2.22) совпадают с полученными в [2], т.е. известное решение предварительно напряжённого стержня является частным случаем общего решения предварительно напряжённого стержня с конструктивным зазором.
Суммарная величина площади " жёсткого " и высокопрочного гибкого элементов и отнесённая к продольной силе имеет вид:
= | k1 - (m - 1) - m (α + 1) |
| [( + 1) (k1 - m) - m · α] · R1 |
(2.22)
Для предварительно напряжённого стержня с конструктивным зазором на величину площади "жёсткого" и гибкого высокопрочного элементов оказывает влияние величина зазора "f" (параметр α).
Величина снижения масса может превышать 50% (см. рис. 2.11 -2.12), эффект снижения массы увеличивается с увеличением значения усилия предварительного напряжения и размера конструктивного зазора.
И если для стержня без конструктивного зазора при фиксированных значениях параметров предварительного напряжения отношения модулей упругости т = Е1/Е2 и переменных значениях параметра отношения прочностных характеристик высокопрочного гибкого и "жёсткого" элементов K1 = R2/Ri (рис. 2.12) величина массы остаётся постоянной, то для стержня с конструктивным зазором при фиксированных значениях параметров σ01/R1, α, т больший эффект снижения массы будет для стержней с меньшими значениями параметра "k".
Регулируя величины предварительного напряжения и конструктивного зазора, можно желаемым образом перераспределить усилие между "жёстким" и гибким элементами.
Зависимость, выражающая отношение площадей гибкого и "жёсткого" элементов имеет вид:
c = | σ01 |
| σT1(k1 - m) - m(σ01 + σT1 · α) |
(2.23)
77
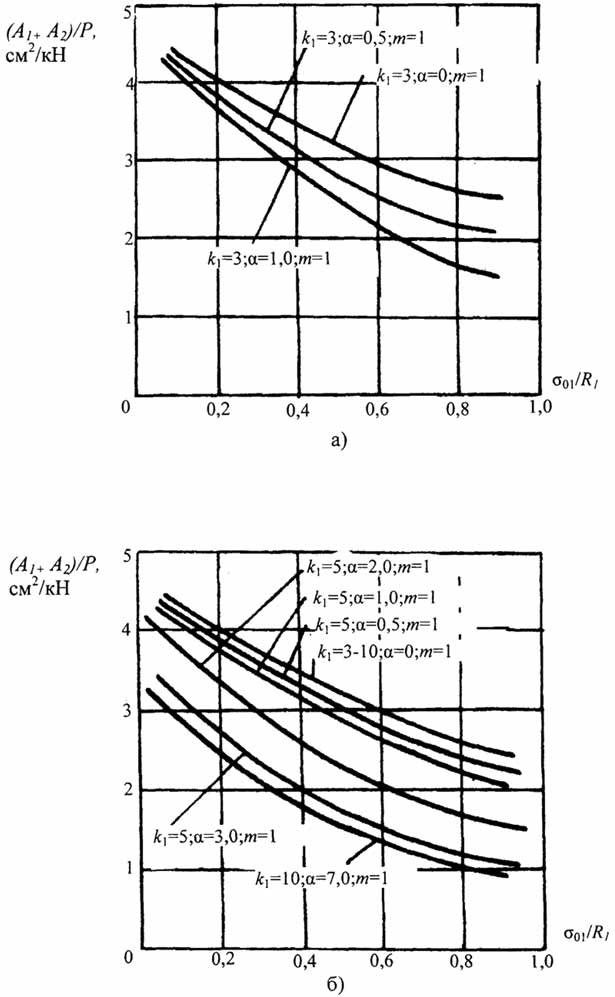Рис.2.11. Зависимость параметров от величины при фиксированных значениях k1; α; m, а - кривые при k1 = 3 и разных а; б - кривые при k1 = 5 и разных α
78
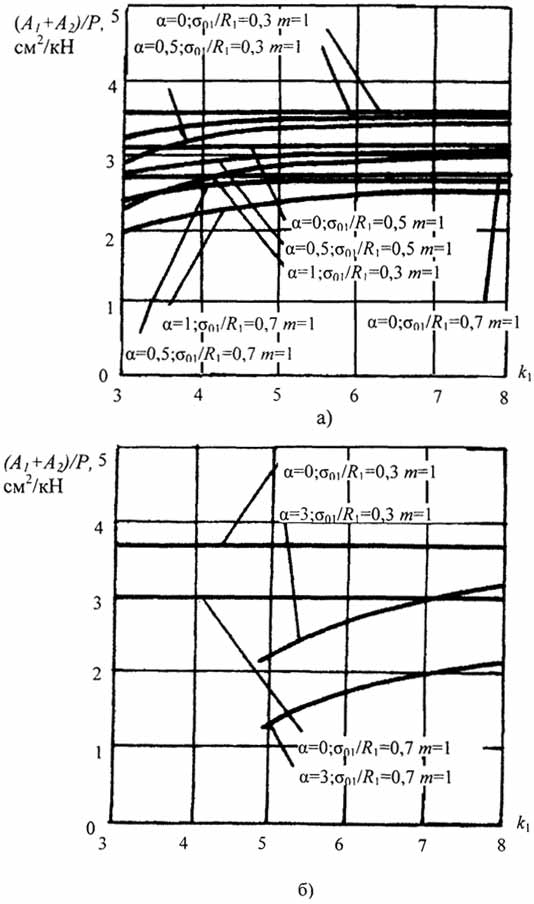Рис.2.12. Зависимость параметров от величины k1 при фиксированных значениях ; α; m, а - кривые при σ01/R1 = 0,3; σ01/R1 = 0,5 и переменных α; б - кривые при σ01/R1 = 0,7 и переменных α
79
Сравнивая формулы (2.12) и (2.23) видим, что они отличаются выражениями включающими α при α = 0 частный случай обыкновенного или предварительно напряжённого стержня.
Величина "с" по выражению (2.23) больше полученной по (2.12) при соответственно равных значениях всех параметров и α ≠ 0, следовательно, и несущая способность такого стержня больше. Работа такого стержня в стержневой системе эквивалентна работе стержня с нелинейной (билинеарной) диаграммой поведения материала.
Показанные свойства поведения элементов под нагрузкой могут наиболее эффективным образом использоваться в составе стержневых систем для различных материалов металлов, дерева, железобетона, пластмасс и т.д., перераспределяя благоприятным образом усилие между отдельными стержневыми элементами и максимально используя их прочностные характеристики при работе на растяжение или сжатие. Для стержневых систем, загруженных динамической нагрузкой представленные стержни могут дополнительно выполнять функции демпфера.
80
