Рассмотрим работу стержня, состоящего из двух материалов загруженного растягивающей силой (рис 2.2). Причём, один из материалов является обычной строительной сталью с явно выраженной площадкой текучести и пределом текучести σt1, другой - высокопрочная сталь с условным пределом текучести σt2 Для таких сталей соотношения между прочностными характеристиками колеблются в пределах σt2 = (4 - 9) · σt1. Следует отметить, что для высокопрочных элементов, выполненных из канатов, модуль упругости материалов составляет (65 - 90)% от модуля упругости строительной стали [2], [46].
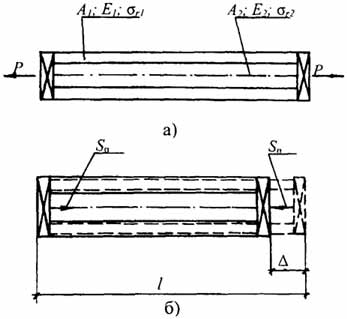 Рис 2.2. Стержень с различными прочностными характеристиками материалов, загруженный растягивающей силой: а - работа под нагрузкой, б - работа после снятия внешней нагрузки.
Рис 2.2. Стержень с различными прочностными характеристиками материалов, загруженный растягивающей силой: а - работа под нагрузкой, б - работа после снятия внешней нагрузки.
Несущая способность такого стержня может быть определена с учётом критерия исчерпания несущей способности входящих материалов (предельное состояние). Если предельные напряжения в элементе ограничены пределом текучести at и развитие пластических деформаций не допускается, то без предварительного напряжения в таких стержнях использование высокопрочных сталей нецелесообразно. Если развитие пластических деформаций в менее прочном "жёстком" элементе допускается, то несущая способность таких стержней может быть определена по формуле
Ртаx = A1 · σT1 + A2 · σЕ2
(2.4)
где Ртах - максимальная несущая способность стержня; А1, А2 - площади сечения соответственно менее прочного материала "жёсткого" элемента и более прочного гибкого элемента стержня; σT1,σT2 - пределы текучести "жёсткого" и гибкого элементов.
68
После снятия нагрузки вследствие развития пластических деформаций в "жёстком" и гибком элементах стержня появляются остаточные напряжения.
Определим величину напряжений, при которых материалы работают упруго (рис. 2.2,6.).
Условие равновесия после снятия внешней нагрузки имеет вид
Sd = σT2 · A2 - σT1 · A2 · m
(2.5)
E1 · A1 · εΔ = Sd - E2 · A2 · εΔ
(2.6)
где Sd - усилие, действующее на стержень после снятия внешней нагрузки.
Е1, Е2 - модули упругости материалов "жёсткого" и гибкого элементов стержня.
Подставляя значение усилия из (2.5) в (2.6), найдём величину относительной деформации самонапряжения εΔ и напряжения в элементах стержня.
εΔ = | c · σT1 · (k - m) |
| E1 · (1 + c · m) |
(2.7)
σ1 = | c · σT1 · (k - m) |
| 1 + c · m |
(2.8)
σ2 =
(2.9)
где σ1, σ2 - напряжение в "жёстком" и гибком элементах стержня после снятия внешней нагрузки.
Остаточное напряжение в сжатом стержне не должно превышать предельного значения из условия обеспечения устойчивости, тогда напряжение в высокопрочном растянутом элементе ограничено величиной
σ2пред = | (1 + c · m) · σкр + σT1 · c · m |
| c |
(2.10)
где σ2пред - предельно-допустимое напряжение в высокопрочном гибком элементе;
σкр - критическое напряжение в "жёстком" сжатом элементе.
Предельная несущая способность стержня
P'max = A1 · σT1 + A2 · σ2пред
(2.11)
т.е. меньше полученной из условия полного развития пластических деформаций.
Запишем выражение для отношения площадей сечения элементов стержня c = A2/A1, при котором прочностные характеристики материалов используются полностью, т.е. в "жёстком" и гибком элементах при деиствии
69
внешней нагрузки напряжения достигают предела текучести, а после снятия нагрузки в "жёстком" элементе остаточное напряжение не превышает критической величины.
c = | σ1кр |
| σT1(k - m) - m · σ1кр |
(2.12)
На рис. 2.3 представлены графики, иллюстрирующие изменение величин сжимающих (растягивающих) напряжений в сжатом и растянутом элементах после снятия внешней нагрузки, в зависимости от соотношения площадей материалов, а также значения предельных напряжений σ2пред для различных величин критических напряжений в "жёстком" элементе.
Как видно из рис. 2.3 и формул (2.9), (2.12), для материалов с характеристиками к = 5 и m = l только при значениях с не превышающих 0,33 остаточное напряжение меньше 210МПа, т.е. при увеличении с материал используется нерационально. Так, например, при с=1 для стержня, у которого σкр = 0.5 · σT, используется менее 50% несущей способности высокопрочного материала для того, чтобы после снятия внешней нагрузки остаточное напряжение не превышало критического значения.
На рис. 2.4 отображены предельные значения напряжения в гибком элементе, обеспечивающие сохранение устойчивости стержня после разгрузки.
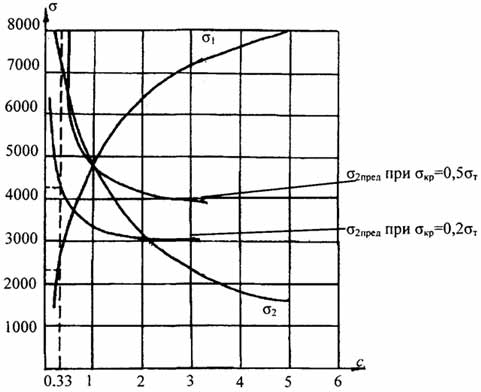 Рис. 2.3. Остаточные напряжения в жестком и гибком элементах стержня
Рис. 2.3. Остаточные напряжения в жестком и гибком элементах стержня
70
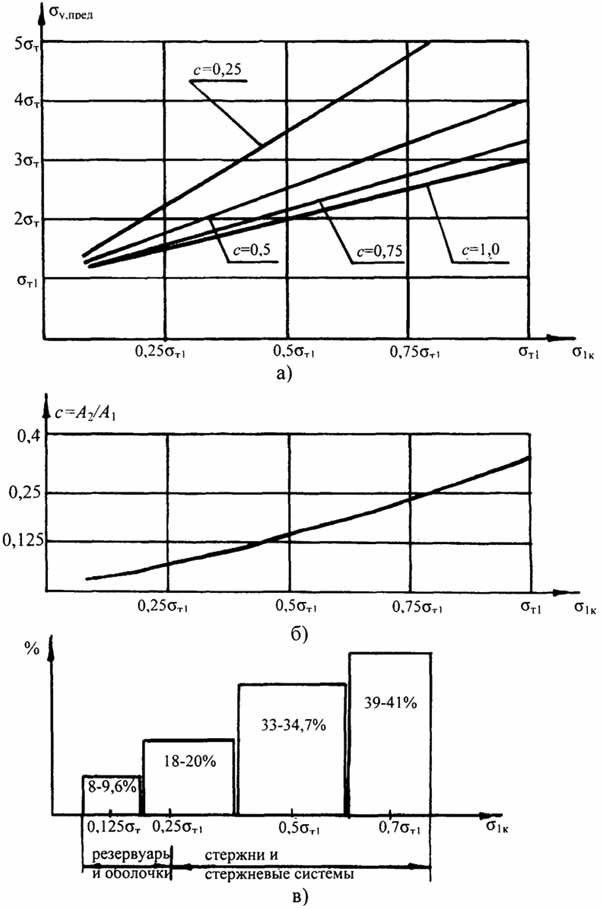 Рис.2.4. Работа под нагрузкой стержней, включающих материалы различной прочности: а - предельные значения напряжения в гибком элементе при условии обеспечения устойчивости стержня; б - соотношение площадей жесткого и гибкого элементов при котором устойчивость стержня обеспечения; в - наибольшая возможная величина снижения массы стержней, включающих материалы различной прочности
Рис.2.4. Работа под нагрузкой стержней, включающих материалы различной прочности: а - предельные значения напряжения в гибком элементе при условии обеспечения устойчивости стержня; б - соотношение площадей жесткого и гибкого элементов при котором устойчивость стержня обеспечения; в - наибольшая возможная величина снижения массы стержней, включающих материалы различной прочности
71
На рис. 2.4,6 приведён график, показывающий соотношение площадей "жёсткого" и гибкого элементов, при котором устойчивость стержня обеспечена. Величина такого соотношения даже при σкр, достигающем предела текучести, менее 0.4. Всё это говорит об ограничении эффективности использования высокопрочных сталей.
Применение предварительного напряжения для таких стержней не изменит их несущую способность, а только даст возможность при загрузке и разгрузке избежать пластических деформаций в "жёстком" элементе, т.е. расширить область упругой работы "жёсткого" элемента.
Аналогичная зависимость получается и для конструкций, включающих материалы с различными прочностными характеристиками.
На рис. 2.4, в показаны наибольшие возможные величины снижения массы стержней и элементов конструкций, включающих материалы различной прочности. Эффект снижения массы повышается с увеличением параметра критического напряжения сжатия при разгрузке конструкции или стержня. Максимальное снижение расхода материала может достигнуть 30 - 40% для стержней и стержневых систем с высокими значениями σкр. В стальных предварительно напряжённых или двухслойных оболочках, σкр для которых в пределах (0.05 - 0.15) R, уменьшение расхода материала не превышает 10%, что очень мало и, как правило, не покрывает затрат на изготовление такой конструкции.
С учетом особенностей работы стержней с различными прочностными характеристиками материалов предлагается новый подкласс предварительно напряжённых конструкций, принцип работы которых под нагрузкой излагается ниже и поясняется на примере предварительно напряжённого стержня с конструктивным зазором или с временно выключающимися связями [35],[86].
72
