Вопросу исследования напряжённого состояния анкеров посвящены работы целого ряда авторов [31] - [33] и другие. Подобные исследования связаны как с постановкой экспериментов, так и с использованием той или иной расчётной модели. Для приближённого расчёта гильзы стакана автором [31] был предложен относительно простой способ, в основу которого положено, что давление р на стенку гильзы распределяется линейно. Максимальное значение у начала входа каната и минимальное, равное нулю, - в конце анкерного стакана (рис. 1.52). Изменение давления по длине отражается уравнением
p = p0 ·
(1.33)
Бесконечно малый элемент площади стенки конуса
dA = 2 · π · r · dy = 2 · π · (r0 + (r1 - r0)) · dy
(1.34)
Сила dP, действующая на единичный элемент площади dA (рис. 1.53)
dP = р · dA
dP = 2 · π · (r0 + (r1 - r0) · p0 · · dy
(1.35)
55
Рис. 1.52. Распределение давления Р на стенку гильзы анкера
Осевая составляющая силы имеет вид
dS = dP · (Sin α + π· Cos α)
(1.36)
Или, подставляя значение для dP из уравнения (1.35), получим
dS = 2 · π · pо · (r0 +(r1 - 2 · r0) · - (r1 - r0) · × (Sin α + μ··Соs α ·) · dy
(1.37)
Интегрируя выражение (1.37), получим
S = 2 · π · p0 · (y · r0 + (r1 - 2 · r0) - (r1 - r0) · l2) × (Sin α + μ · Cos α)
(1.38)
или для всей гильзы при у = l
S = 2 · p0 · ( + ) · l · (Sin α + μ · Cos α)
(1.39)
Давление р с учётом уравнения (1.38) имеет вид
p = ·
S |
| 2 · π · ( + ) · l · (Sin α + μ · Cos α) |
(1.40)
Тангенциальное напряжение а, по внутренней поверхности гильзы на расстоянии у от начала координат
σt = p ·
(1.41)
Здесь величина р принимается из уравнения (1.40). При опирании анкерного стакана на нижнюю поверхность осевое давление
σy =
(1.42)
где величина S принимается из уравнения (1.39). При проведении исследований автор [30] принимал коэффициент трения μ = 0,2, последующие исследования
56
[32] показали, что величина этого коэффициента значительно больше и может быть принята μ = 0,5. Подробные исследования напряжённого состояния анкеров выполнены Шуманом [31]. Им изучалась работа под нагрузкой конуса заливки, деформации анкерной гильзы с учётом упругого и пластического поведения металла заливки. Показано, что для свинцово-оловянного сплава металл заливки на выходе из конуса пластичен, причём конус с малым углом эту тенденцию усиливает. Для цинковых сплавов установлено, что для подавляющего числа конусов (канаты больших и средних диаметров) материал заливки работает упруго. Соединение между металлом заливки и проволокой сохраняется по всей длине. Это показало, что длина заливки может быть значительно уменьшена.
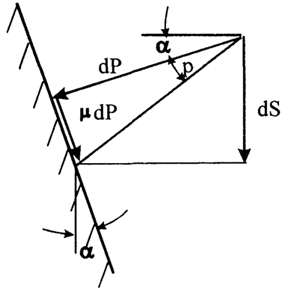Рис. 1.53. Сила dP, действующая на единичный элемент площади dA
где μ - коэффициент трения.
Испытания конуса с D0=1,8d, уклоном стенки 1:10 (уклон конуса 1:5) и длиной заливки L=2,5d, материал ZnA16Cu1 (Цамак) показали хорошие результаты при широком спектре динамических загружений.
Определённый интерес представляет собой знание величин предельных температур, при которых заливные анкеры надёжно обеспечивают передачу нагрузки. Подобные исследования были проведены авторами [34], загружение осуществлялось статической нагрузкой при постоянном значении силы F=0,5 · FW (50% от величины разрушающего усилия для каната), температура повышалась ступенями. При проведении испытаний регистрировались изменения температуры, деформации ползучести и время.
Выдержка под нагрузкой при постоянной температуре одной ступени составляла 15 часов.
Проведены сравнения скорости ползучести для различных материалов заливки. В табл. 1.2 приведены значения температур для различных материалов заливки, при которых скорость ползучести достигает 0.01 мм / час.
57
Длительные испытания сплава ZnA16Cu1 показали, что при температуре 150°С скорость ползучести в 10 раз больше, чем при нормальной температуре. При изменении нагрузки деформация не затухает.
Таблица 1.2.
Значения температур, при которых скорость ползучести канатов в анкерах достигает 0.01 мм / ч, и граничные температуры практического применения
| Материал заливки |
Температура Т°С , при которой скорость ползучести составляет 0.01 мм / ч |
Граничная температура Т°С практического применения |
| Свинцово-оловянный сплав VgPbSn10Sb10 |
≈ 105°С |
≈ 80°С |
| Оловянный сплав SnSbl2Cu6Pb |
≈ °С |
≈ 60°С |
| Цинковый сплав GB-ZnA16Cu1 |
≈ 180°С |
≈ 120°С |
| Чистый цинк |
≈ 165°С |
≈ 120°С |
| Полиэстровая смола А |
≈ 48°С |
40°С |
| Полиэстровая смола В |
≈ 80°С |
≈ 60°С |
58
