Глава 2
МЕТОДЫ ЭКОЛОГИЧЕСКИХ ИССЛЕДОВАНИЙ
Методы экологических исследований можно разделить на две основные группы:
- математические методы исследования и прогнозирования экологических ситуаций;
- экспериментальные методы мониторинга окружающей среды.
Благодаря широкому использованию ЭВМ математические методы получили в настоящее время широкое распространение. В основе этих методов лежит компьютерное исследование модели экологической системы. Модель - упрощенное представление реальной системы, для которой характерно бесконечное число связей с окружающей средой. Упрощение позволяет ограничить число связей и выбрать те из них, которые нам представляются наиболее важными. Далее с помощью ЭВМ осуществляются компьютерное моделирование (исследование) динамики поведения системы в различных ситуациях и прогнозирование ее поведения в будущем.
Моделирование позволяет определить основные свойства модели экологической системы, законы развития и взаимодействия с окружающим миром, научиться управлять поведением модели и определить наилучшие способы управления экологической системой для достижения заданных целей, прогнозировать прямые и косвенные последствия реализации разных форм и способов воздействия на экологический объект.
Различают следующие типы математических моделей:
- динамические,
- стохастические,
- оптимизационные и игровые.
Динамические модели описываются обыкновенными дифференциальными уравнениями или матричными уравнениями и не содержат случайных параметров.
Стохастические модели в той или иной форме учитывают случайные параметры, имеющиеся в реальных системах.
Оптимизационные и игровые модели предназначены для поиска оптимальных стратегий поведения или воздействия на экологические системы.
13
В качестве примера динамической модели рассмотрим поведение во времени (динамику) некоторой популяции.
В современной экологии часто возникает вопрос: как определить численность той или иной популяции через определенное время? Ответ на него не только представляет теоретический интерес, но и имеет большое практическое значение. Действительно, не зная этого, нельзя правильно планировать эксплуатацию различных возобновляемых природных ресурсов - промысловых рыб, охотничьих угодий и т.п. Может ли в решении этого вопроса помочь математика? Оказывается, да. Рассмотрим некоторые простейшие модели и проиллюстрируем на них подход к данному вопросу.
Пусть некоторая популяция имеет в момент времени t0 биомассу х0. Предположим, что в каждый момент времени скорость увеличения биомассы пропорциональна уже имеющейся биомассе, а борьба за источники питания и самоотравления снижают биомассу пропорционально квадрату наличной биомассы. Если обозначить биомассу в момент времени t через x(t), а изменение ее за время Δt через Δх, то можно записать следующее приближенное равенство:
Δx ≈ (kx - αx2)Δt,
(2.1)
где α и k - положительные постоянные (параметры).
В дифференциальной форме это соотношение имеет вид:
(2.2)
Оно и представляет собой математическую модель процесса изменения биомассы популяций. В литературе по экологии уравнение (2.2) часто называют логистическим.
Если теперь поставить вопрос о том, какова же будет биомасса в момент времени t, то можно воспользоваться математической моделью, решая задачу Коши для уравнения (2.2) с начальным условием (2.3):
x(t0) = x0.
(2.3)
Возвращаясь к исходному уравнению (2.2), заметим, что если x0 =
, то задача Коши имеет решение
x(
t)≡
x0. Если
x0 <
, то
(2.4)
Если x0 <
, то аналогично предыдущему случаю снова получаем формулу (2.4), откуда вытекает, что при
x0 <
график функции
14
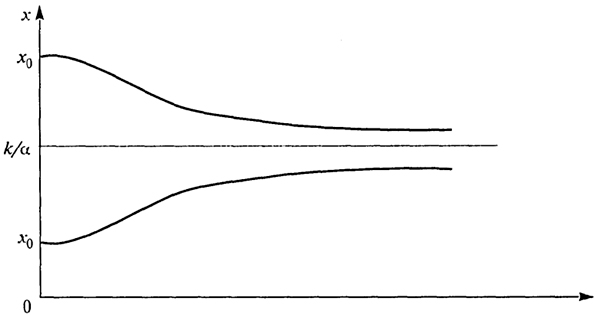
Рис. 2.1. Зависимость биомассы от времени для различных значений параметров
k, α и х
0
x(t) монотонно возрастает, а при x0 >
- монотонно убывает, причем оба графика (рис. 2.1) имеют горизонтальную асимптоту
Мы рассмотрели весьма упрощенную ситуацию, так как предполагали, что популяция не взаимодействует с другими популяциями, учет же этого обстоятельства, конечно, значительно усложняет модель.
Рассмотрим одну из таких моделей. Будем обозначать биомассы двух популяций через х и у соответственно. Предположим, что обе популяции потребляют один и тот же корм, количество которого ограниченно, и из-за этого находятся в конкурентной борьбе друг с другом.
Французский математик В. Вольтерра в 1926 г. показал, что при таком предположении динамика популяций достаточно хорошо описывается следующей системой дифференциальных уравнений:
(2.6)
где k1, k2, ε1, ε2, λ1, λ2 - определенные положительные числа. Первые члены правых частей системы (2.6) характеризуют скорость роста популяций при отсутствии ограничивающих факторов. Вторые члены учитывают те изменения в скоростях, которые вызываются ограниченностью корма.
15
Задавая различные значения параметров, с помощью системы (2.6) можно описать взаимодействие двух популяций, одна из которых - хищник, а другая - жертва.
Если > , то вторая популяция вымирает: y(t) → 0, t → ∞, а первая стабилизируется: x(t)→
,
t → ∞. Если же
< , то имеем обратную картину: первая популяция вымирает:
x(
t) → 0,
t → ∞, а вторая стабилизируется:
x(t)→, t → ∞.
В дальнейших рассмотрениях будем для простоты считать, что k1 = k2 = k и ε1 = ε2 = ε. Тогда, деля второе уравнение системы (2.6) на первое, получим =
, откуда
(2.7)
Обе популяции не вымирают и численность их стабилизируется к значениям, которые можно найти как координаты пересечения прямых у* = (у*1,…,y*m) ∈ Y и y =
x, откуда
(2.8)
С помощью детерминистских моделей изучают различные по характеру процессы, происходящие в реальной среде, как, например, отдельные типы экологических взаимодействий "паразит-хозяин" и др.
Одну из простейших математических моделей для системы "паразит-хозяин" в динамике численности насекомых разработал в 1925 г. А. Лотки, который вывел следующие уравнения:
(2.9)
где х - численность популяции хозяина; у - численность популяции паразита; r1 - удельная скорость увеличения популяции хозяина; d1 - удельная скорость гибели популяции паразита; p1 и р2 - константы. График процесса, построенный по таким уравнениям, обнаруживает, что в результате взаимодействия двух видов должны возникать осцилляции (колебания) с постоянной амплитудой, которая зависит от соотношения между скоростями увеличения численности двух видов (см. рис. 2.2).
В то же время математик В. Вольтерра выявил сходные закономерности для системы "хищник - жертва", обрабатывая статистические
16
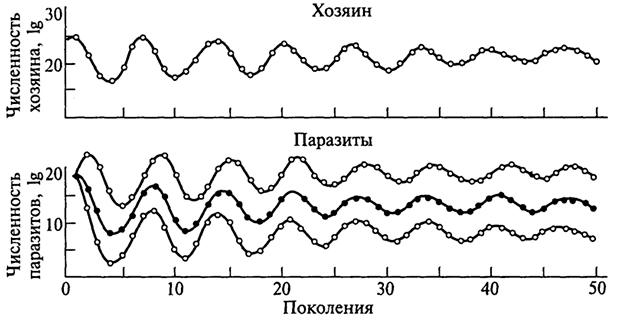
Рис. 2.2. Расчетная модель, показывающая устойчивое сосуществование хозяина и трех паразитов
данные рыбного промысла. Один из выведенных им законов - "закон периодического цикла" - гласит, что процесс уничтожения одного вида другим может привести к периодическим колебаниям численности популяций обоих видов, зависящих только от коэффициентов роста популяций хищника и жертвы и от исходной относительной численности.
В реальных экологических системах возникают не только периодические, но и хаотические колебания численности популяций, которые изучает новая наука, возникшая во второй половине XX века синергетика - наука о хаосе и упорядоченных движениях в динамических системах.
Однако рассмотренная выше детерминистская модель не может служить точным отражением реальной экологической системы: во-первых, она допускает бесконечно большую численность популяции; во-вторых, не учитывает случайных колебаний, происходящих в среде во времени.
В качестве еще одного примера детерминистской модели рассмотрим уравнение
(2.10)
где N - число особей в момент времени t, α - истинная скорость роста.
Решением этого уравнения, удовлетворяющего начальному условию
N(0) = N0
(2.11)
является функция
N(t) = N0eat
(2.12)
17
(так называемый закон Мальтуса - закон роста популяции без конкуренции). В основе главного допущения здесь лежит то, что за короткий промежуток времени t каждая особь порождает αΔt новых особей.
Рассмотрим теперь модель, учитывающую случайные изменения среды. Простейшая модель, соответствующая уравнению (2.10), имеет вид
(2.13)
где y(t) - случайная величина со средним значением, равным нулю. Решение задачи [уравнение (2.13) при условии (2.11)] имеет вид
(2.14)
Нас интересуют следующие вероятностные характеристики: ожидаемое значение, т.е. среднее значение популяции в момент времени /и вариация (дисперсия), т.е. среднее квадратичное отклонение от N(t).
Чтобы придать смысл интегралу 
от случайной величины (y)t, сделаем некоторые упрощающие предположения. Будем считать, что y(t) - ступенчатая функция: y(t)=yi при i-1≤t≤i = 1, 2, ... . При этом все случайные величины имеют нормальное распределение. Нормальный закон распределения (иногда называемый законом Гаусса) наиболее часто встречается на практике. Многие встречающиеся на практике случайные величины, такие, например, как ошибки измерений, могут быть представлены в виде суммы большого числа сравнительно малых слагаемых - элементарных ошибок, каждая из которых вызвана действием отдельной причины, не зависящей от остальных. Каким бы законам распределения ни были подчинены элементарные ошибки, особенности этих распределений в сумме большого числа слагаемых нивелируются, а сумма оказывается подчиненной закону, близкому к нормальному. Например, проводя измерения длины листьев в лесу, мы имеем случайную величину X - длину листьев. Вероятность того, что X < х, т.е. Р = {Х<х}, называется функцией распределения случайной величины и обозначается через F(x), а ее производная F'(x) = ƒ(x) - плотностью распределения и в случае нормального закона распределения имеет вид (рис. 2.3)
(2.15)
18
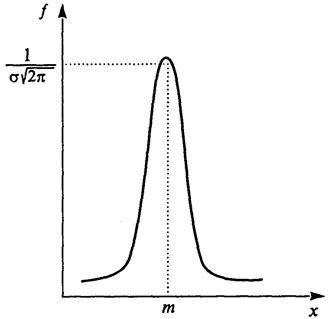
Рис. 2.3. График плотности распределения по нормальному закону
Численные параметры т и σ - это математическое ожидание (среднее значение) Е[уi] и среднее квадратичное отклонение D [уi] случайной величины X.
Откуда для среднего значения N(t) получаем выражение
N(t) = N0eatE(ey1+y2+...yt) = N0eatПi=1 E[eyi ]=N0eat
(2.16)
и коэффициент вариации при t →∞ равен
(2.17)
Из формул (2.16) и (2.17) следует, что хотя, как и в детерминистском случае, среднее значение N(t) экспоненциально возрастает, экспоненциально возрастают и отклонения от среднего значения. Таким образом, с течением времени колебания численности популяции становятся все более резкими. В этом отражается то обстоятельство, что детерминистская система не имеет стационарного состояния, более того, при определенных соотношениях между я и о вероятность ее вымирания приближается к единице.
Выше рассмотрены простейшие модели динамики популяций с учетом конкуренции за пищевые ресурсы. Эти модели можно использовать для качественного анализа роста народонаселения. Конечно, рост численности населения сильно различается в разных странах, и даже в развитых странах темпы роста неодинаковы. Например, в Дании, Швеции, Германии, Австрии этот показатель колеблется около нулевого значения. В таких странах, как Италия, Польша, Канада, США, рождаемость пока еще превышает смертность. Однако в целом в большинстве развитых стран ежегодный прирост населения составляет примерно 0,5% в год, тогда как в развивающихся странах - 2,1 % в год.
В целом происходит стремительный рост населения на планете, поэтому проблема управления природными ресурсами становится жизненно важной. Все отрасли управления ресурсами объединяет одна наука - экология, одна общая проблема - проблема оптимизации расходования ресурсов и, наконец, необходимость использовать
19
одни и те же методы - выборки, статистический анализ, математический анализ, логические процедуры, связанные с исследованием операций и анализом систем, применение вычислительной техники. Конечно, анализ и решение такой глобальной проблемы и даже какой-либо ее части представляют собой труднейшую задачу.
Начнем с рассмотрения простейшей задачи об оптимальном рационе, математическая модель которой допускает наглядную геометрическую интерпретацию. Пусть имеется п продуктов питания (хлеб, мясо, молоко, картофель и т.д.) и т полезных веществ (жиры, белки, углеводы и т.п.). Обозначим через аij - содержание i-го вещества в единице j-го продукта, через bi - потребность индивида в i-м веществе (скажем, в месяц) и через Cj - цену единицы j-го продукта.
Обозначив потребление индивидом j-го продукта через xj, получаем задачу о выборе наиболее дешевого рациона питания (стоимости месячной продовольственной потребительской корзины):
(2.18)
при ограничениях
(2.19)
и
xj ≥ 0, j = 1,2, …, n.
(2.20)
Такая задача называется задачей линейного программирования (в стандартной форме)1.
Часто возникают ситуации, в которых различные участники имеют не совпадающие между собой интересы. Математические модели и методы для исследования таких так называемых конфликтных ситуаций получили название теории игр.
Приведем простейшие понятия и результаты этой теории. Под словом "игра" понимается совокупность правил, руководствуясь которыми игроки-участники принимают решения. Предположим, что результатом игры является плата, которую в соответствии с правилами проигравший участник платит выигравшим. Для простоты ограничимся сначала так называемыми "играми двух лиц с нулевой суммой". Для того чтобы полностью определить такую игру, нужно задать таблицу платежей - платежную матрицу, например, следующую матрицу размером 3×4:
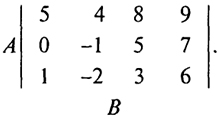
20
Эта запись означает, что игрок А выбирает одну из строк этой матрицы, а игрок В, не зная выбора А, выбирает один из столбцов матрицы. Число на пересечении выбранных строки и столбца определяет выигрыш первого игрока (соответственно проигрыш второго). Например, если А выбрал вторую строку, а В - третий столбец, то А выиграл 5 единиц, а В их проиграл. Если же А выбрал третью строку, а В - второй столбец, то А проиграл 2 единицы, а В их выиграл.
Будем считать, что цель каждого из игроков состоит в максимизации наименьшего возможного выигрыша (соответственно минимизации наибольшего возможного проигрыша). Основной вопрос, возникающий в теории игр: существует ли наилучший способ игры у каждого из игроков, т.е. имеются ли у них оптимальные стратегии?
Прежде чем сформулировать ответ, вернемся к рассматриваемой матрице. Сразу видно, что игроку А выгоднее всего выбрать первую строку, ибо все ее элементы больше соответствующих элементов остальных строк. Точно так же игроку В выгоднее всего выбрать второй столбец, поскольку все элементы этого столбца меньше соответствующих элементов остальных столбцов. Следовательно, в данном примере оптимальными стратегиями будут следующие: для А - выбор первой строки, а для В - выбор второго столбца. Число 4, стоящее на пересечении первой строки и второго столбца, носит название цены игры, т.е. платы, которую получает оптимально играющий игрок. Таким образом, в этом примере гарантированный выигрыш А - не менее 4 единиц и гарантированный проигрыш В - не более 4 единиц (он равен 4 единицам, если оба игрока играют оптимально).
Если оказывается, что для данной платежной матрицы минимум в какой-либо строке совпадает с максимумом в каком-либо столбце, то эти строка и столбец называются оптимальными, а их пересечение - седловой точкой платежной матрицы. Соответствующее число и будет ценой игры.
Однако далеко не каждая матрица имеет седловую точку. Например, матрица 
седловой точки не имеет. Говорить здесь о максимизации наименьшего возможного выигрыша (минимизации наибольшего возможного проигрыша) можно только при использовании так называемой смешанной стратегии при многократной игре с одной и той же платежной матрицей. Суть этой стратегии заключается в выборе разных стратегий с определенными частотами. Итак, пусть А выбирает первую строку с частотой х, а вторую - с частотой (1 - х). Аналогично для В соответствующие частоты обозначим через у и (1 - у). Тогда средний выигрыш А, обозначаемый через Е(х, у), равен
21
Е(х, у) = 4(1 - х)у + х(1 - у) = х + 4у - 5ху.
(2.22)
Нас интересует величина maxx min y Е (х, у). Имеем
E = 4 - 5x,
(2.23)
откуда Еy > 0 при 0 ≤ x <
, Е
у = 0 при x = 4/5 и
Еу < 0 при
<
x ≤ 1.
Значит
(график на рис. 2.4).
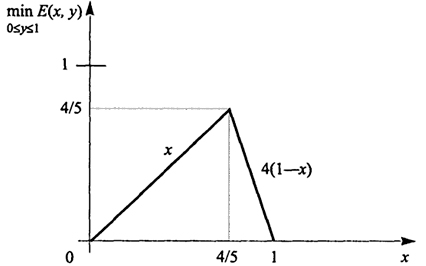
Рис. 2.4. График функции min
Е(х, у) 0 ≤
i ≤ 1
Следовательно,
(2.24)
и оптимальной смешанной стратегией для А будет выбор первой строки с частотой 4/5 и второй строки с частотой 1/5. Средний проигрыш B, обозначаемый F(x, у), очевидно равен - Е(х, у). Нас интересует величина
maxx miny F(x, y)
, где
F(x, у) = 5ху - х - 4у.
Имеем Fx = 5у - 1, откуда F(x) < 0 при 0 ≤ y <
,
Fx = 0 при
у = 1/5 и
Fx > 0 при
<
y ≤ 1. Значит
22
(график на рис. 2.5)
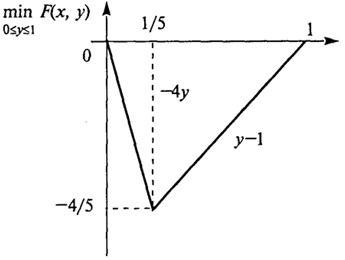
Рис. 2.5. График функции min
F(x, у) 0 ≤ y ≤ 1
Следовательно,
и оптимальной стратегией для В будет выбор первого столбца с частотой 1/5 и второго столбца с частотой 4/5.
При оптимальных смешанных стратегиях выигрыш А и соответственно проигрыш В в пять раз меньше максимально возможного при одиночной игре.
Отметим также, что в рассмотренном примере мы показали существование оптимальных стратегий и установили равенство
при этом величину Е(х, у) можно трактовать как математическое ожидание выигрыша, а величину ν = 4/5 определить как цену игры.
Рассмотрим теперь общий случай прямоугольной матрицы
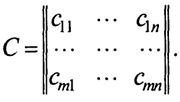
23
При любой допустимой стратегии игрока А: х1 ≥ 0, ..., хт ≥ 0, x1 + x2 + хт = 1 и любой допустимой стратегии игрока В: y1 ≥ 0, ..., уn ≥ 0, y1 + у2 + ... + ут = 1 математическое ожидание выигрыша равно
(2.25)
Множество допустимых стратегий х = (х1 ..., хn) игрока А обозначим через X, а множество допустимых стратегий у = (у1, ..., уn) игрока Б обозначим через 7
Рассмотренные выше примеры являются частными случаями общих теорем для игр с прямоугольными матрицами (прямоугольными играми). Из них, в частности, вытекает следующее.
1. Величины
maxx∈ X miny∈ Y E(x, y) и
maxy∈ Y minx∈ X E(x, y) существуют и равны между собой. При этом величина
maxx∈ X miny∈ Y E(x, y) =
maxy∈ Y minx∈ X E(x, y) =
ν
(2.26)
является ценой игры.
2. Всякая прямоугольная игра имеет цену; каждый игрок в прямоугольной игре всегда имеет оптимальную стратегию.
3. Пусть Е - математическое ожидание выигрыша в прямоугольной игре с матрицей С, имеющей цену ν. Тогда для того чтобы элемент х* = (х1*, ..., хт*) ∈ X был оптимальной стратегией для игрока А, необходимо и достаточно, чтобы для всякого j = 1, 2, ..., п базисного вектора у(i) = (0, ..., 0, 1, 0, ..., 0) имело место неравенство
ν ≤ E(x*, у(i)).
(2.27)
Аналогично, для того чтобы элемент у* = (у1*, ..., y1*) ∈ Y был оптимальной стратегией для игрока В, необходимо и достаточно, чтобы для всякого элемента базисного вектора х(i) = (0,..., 0, 1,0,...,0) имело место неравенство
E(x(i), y*) ≤ ν
(2.28)
24
1
Общую теорию см.:
АшмаковС.А. Линейное программирование. - М., 1981. 20
