Расчетная схема нитей до их загружения временной нагрузкой приведена на рис. 8.37, а. За счет предварительного напряжения системы растяжки (распорки) передают на несущую и стабилизирующую нити равномерно распределенную линейную нагрузку интенсивностью q0. Величину этой контактной нагрузки назначают так, чтобы при появлении временной нагрузки р, которая будет догружать несущую нить и разгружать стабилизирующую, как показано на схеме рис. 8.37, б, последняя не выключалась из работы.
Изменение распора стабилизирующей нити ΔHs при загружении системы какой-нибудь нагрузкой р будет пропорционально изменению распора несущей нити ΔHn от той же нагрузки, т.е.
ΔHs = - α ΔHn.
(8.71)
Поскольку стрелки дополнительных провесов нитей, объединенных растяжками (распорками), при этом изменятся на одинаковую величину, мы можем записать, используя формулы (8.15), (8.71) и принимая во внимание зависимости ΔHn = Δpl2 / (8fn); ΔHs = Δpl2 / (8fs), следующее равенство:
388
ΔHn =
α · ΔHn.
Отсюда найдем коэффициент α
α =
.
(8.72)
При изменении контактной нагрузки на величину q изменятся распоры в несущей и стабилизирующей нитях:
ΔHn =
; ΔHs =
.
(8.73)
Решая совместно уравнения (8.71)...(8.73), определим искомое изменение контактной нагрузки при загружении системы временной нагрузкой р
q = p
.
(8.74)
Для сокращения построений мы проделали преобразования для висячих систем с параллельными нитями. Повторив эти преобразования применительно к системам с радиальными нитями, вы можете убедиться, что конечная формула (8.74) при этом не изменится. В дальнейшем изменения формул для систем с радиальными нитями мы будем оговаривать.
Остаточное натяжение стабилизирующей нити ΔTs ≈ ΔHs принимают в пределах 20...30% от возможного изменения ее начального распора ΔHs.
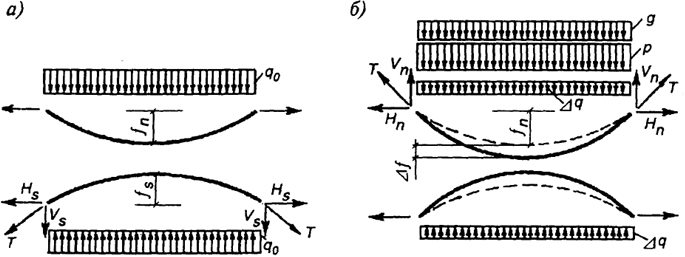 Рис. 8.37. Расчетная схема двухпоясной системы:а
Рис. 8.37. Расчетная схема двухпоясной системы:а - в стадии предварительного напряжения;
б - в стадии действия расчетных нагрузок
389
т.е. остаточную Δq и начальную q0 контактные нагрузки можно назначить равными:
Δq = (0,2...0,3)q; q0 = q + Δq = (1,2...1,3)q.
(8.75)
Дальнейший расчет нитей на прочность не представляет затруднений. Нити рассчитывают независимо одна от другой: несущую нить рассчитывают по общим правилам на нагрузку (g + p + Δq), а стабилизирующую - на нагрузку q0. Если ветровой отсос превышает собственный вес покрытия, то при расчете стабилизирующей нити следует учесть разницу (pw - g), где pw - линейная ветровая нагрузка на нить. С некоторым запасом вы можете передать эту разницу на стабилизирующую нить целиком, т.е. просто добавить ее к нагрузке q0. На самом деле нагрузка (pw - g) будет передаваться на систему нитей, поэтому при более точном расчете нужно найти по формуле (8.74) изменение контактной нагрузки при ветре и выполнить остальные операции.
Отметим еще одно возможное уточнение расчета, которое также не существенно сказывается на изменении конечного результата. Оно связано с учетом изменения стрелок провесов нитей при переходе от одной нагрузки к другой. При этом вначале находят распоры для разных этапов работы системы от нагрузок pi, а затем их алгебраически суммируют. При переходе от состояния i к состоянию i + 1 распор находят по формуле Hi+1 = Mi / fi ± Mi+1 / (fi ± Δfi). Приращение стрелки Δfi от нагрузки pi, можно определить на основании равенства (8.15) по формуле
Δfi = k
| pil4 |
| (1+ αfs / fn) EAnfn2 |
,
(8.76)
где k = 3/128 - для параллельных систем нитей; k = 5/864 - для радиальных систем.
Расчет распорок (растяжек) и опорных конструкций (балок, колец) не имеет особенностей по сравнению с общими правилами расчета элементов стальных конструкций.
Точный расчет висячих покрытий с определением вертикальных и горизонтальных перемещений всех его характерных точек выполняют на ЭВМ. Мы рассмотрели лишь вопросы расчета двухпоясных систем на прочность, что обеспечивает безопасность конструкций покрытия. Однако вопросы его долговечности (в особенности кровли), связанные с деформативностью покрытия, выпали из поля такого рассмотрения. Это объясняется не столько громоздкостью подобных расчетов при разных вариантах загружения покрытия временной нагрузкой, сколько отсутствием
390
научно обоснованных норм ограничения предельных перемещений. В литературе нет единого мнения по этому вопросу, скорее всего следует ориентироваться на предельное приращение стрелки провеса при действии нормативной временной нагрузки, равное 1/200 от пролета. При полном загружении покрытия временной нагрузкой вы можете найти приращение стрелки в середине пролета по формуле (8.76) и сравнить его с указанным предельным значением. Если у вас возникнет желание сделать более обстоятельный анализ деформативности покрытия в разных точках при полном и частичных загружениях его временными нагрузками, то обратитесь к учебному пособию [3] или к специальной литературе.
Последовательность расчета
- Назначьте состав ограждающих конструкций, определите постоянную и временные нагрузки.
- Задайтесь стрелками провесов несущей и стабилизирующей нитей в пределах 1/8...1/20 пролета, ориентируясь на полюбившийся вам аналог, либо выполните вариантное проектирование для разных стрелок, всякий раз повторяя приведенный здесь расчет.
- Задайтесь коэффициентом α = 0,1...0,15 в первом приближении; определите падение контактной нагрузки.
Если покрытие выполнено по схеме а (см. рис. 8.29), то предварительное напряжение целесообразно осуществлять после монтажа ограждающих конструкций, т.е. после приложения постоянной нагрузки g. В этом случае величину контактной нагрузки нужно назначать из условия невыключения из работы стабилизирующих нитей после приложения снеговой нагрузки. Тогда падение контактной нагрузки будет равно
q = p
.
В покрытиях, выполненных по схемам б, в (см. рис.8.29), предварительное напряжение удобно производить до монтажа ограждающих конструкций, при этом величину контактной нагрузки приходится назначать несколько больше, исходя из ее падения при загружении покрытия собственным весом и снегом
q = (g + p)
.
Определив падение контактной нагрузки тем или иным способом, назначьте ее величину
q0 = q + Δq, где Δq = (0,2...0,3) q.
391
4. Подберите в первом приближении сечение стабилизирующей нити из расчета восприятия ей распора от контактной нагрузки1:
Тs = √Hs2 + Vs2; As > 1,6Ts / (kp Run);
- в покрытиях с параллельными нитями
Hs = q0 l2 / 8fs; Vs = q0 l / 2;
- в покрытиях с радиальными нитями
Hs = q0 l2 / 24fs; Vs = q0l / 4.
Если натяжение стабилизирующих нитей осуществляют после приложения постоянной нагрузки, то к контактной нагрузке q0 следует добавить ветровой отсос.
5. Подберите в первом приближении сечение несущей нити:
Tn = √Hn2 + Vn2; An > 1,6Tn / (kp Run);
в покрытиях с параллельными нитями
Hn = (g + p + Δq) l2 / 8fn; Vn = (g + p + Δq) l / 2;
в покрытиях с радиальными нитями
Hn = (g + p + Δq) l2 / 24fn; Vn = (g + p + Δq) l / 4.
При малых стрелках, выполняя первое приближение расчетов по пп. 4, 5, вы можете подбирать сечение нити по распору H, не вычисляя вертикальной составляющей тяжения V. Однако, когда вы будете возвращаться к этим пунктам при точных проверках, нужно ориентироваться на тяжение Т.
6. Вычислите по формуле (8.72) коэффициент α и уточните контактную нагрузку (8.74):
α =
; q = p
; Δq = (0,2...0,3)q; q0 = q + Δq.
Здесь под р понимается временная нагрузка или суммарная нагрузка g + p, в зависимости от условий предварительного напряжения системы (см. п.3).
7. Вернитесь к пп. 4, 5 и повторите изложенные там вычисления при новых значениях контактных нагрузок. Выберите подходящие канаты для несущей и стабилизирующей нитей. Найдите длины исходных заготовок для этих нитей по формуле (8.14)
392

8. Оцените деформативность покрытия в приближенном варианте по формуле (8.76)\
Δfi = k
| pil4 |
| (1+ αfs / fn) EAnfn2 |
≤
l
или выполните более обстоятельный анализ.
9. Определите усилия в распорках N = (g + p + Δq)a или растяжках N = q0a, где а - шаг распорок (растяжек), и подберите их сечение.
10. Определите линейную нагрузку на балки (кольца) опорного контура от распоров несущей и стабилизирующей нитей, назначьте состав и подберите размеры поперечного сечения элементов опорного контура, выполните необходимые проверки на прочность и устойчивость.
Пример 8.4. Рассчитаем двухпоясное покрытие плавательного бассейна, рассмотренного в примере 8.1, но с иным составом ограждающих конструкций, которые примем из профилированного настила, фенольного пенопласта и рулонного ковра [15]. Поперечный разрез здания приведен на рис. 8.38. Шаг нитей - 3 м, шаг распорок - 3 м.
Расчетная постоянная нагрузка (табл. 8.5) составляет 0,52 кН/м2. Линейная постоянная нагрузка на нити g = 0,52 · 3 = l,56 кН/м. Снеговая нагрузка для III снегового района s = 1,0 кН/м2. Коэффициент надежности по нагрузке при отношении нормативной нагрузки от собственного веса покрытия к нормативной снеговой нагрузке 0,52/1,0 = 0,52 < 8 равен γс = 1,6. Расчетная снеговая нагрузка p = 1,6 · 1 · 3 = 4,8 кН/м.
Назначаем стрелки: несущей нити fn = (1/20) l = 3,25 ≈ 3 м; стабилизирующей нити fs = (1/30) l ≈ 2 м. Принимаем в первом приближении коэффициент α = 0,1.
Определяем падение контактной нагрузки при загружении покрытия постоянной и снеговой нагрузками q = (g + p)α fs / (fn + α fs) = 6,36 · 0,1 · 2 / (3 + 0,1 · 2) = 0,4 кН/м.
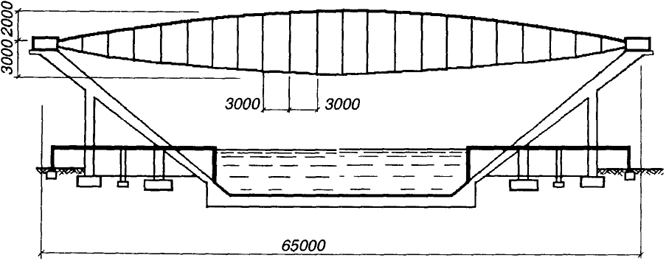 Рис. 8.38. К примеру 8.4
Рис. 8.38. К примеру 8.4
393
Таблица 8.5. Нагрузка на 1 м2 покрытия (к примеру 8.4)
| Состав покрытия |
Нормативная нагрузка, кН/м2 |
Коэффициент надежности по нагрузке |
Расчетная нагрузка, кН/м2 |
| Постоянная нагрузка |
| Гидроизоляция (двухслойный рулонный ковер) |
0,08 |
1,3 |
1,04 |
| Слой припененного рубероида |
0,012 |
1,2 |
0,014 |
| Теплоизоляция (фенольный пенопласт толщиной 5 см, плотностью 60 кг/м3) |
0,30 |
1,2 |
0,36 |
| Стальной профилированный настил Н60-782-1 |
0,133 |
1,1 |
0,146 |
| Стальные канаты и распорки |
0,2 |
1,1 |
0,22 |
| Итого |
0,455 |
- |
0,520 |
| Временная нагрузка |
| Снеговая нагрузка для III района |
1,0 |
1,6 |
1,6 |
| Итого |
1,455 |
|
2,12 |
Принимаем остаточную контактную нагрузку при полном загружении покрытия Δq = 0,25q = 0,25 · 0,4 = 0,1 кН/м, тогда начальная контактная нагрузка будет равна q0 = q + Δq = 0,4 + 0,1 = 0,5 кН/м.
Подбираем ориентировочную площадь сечения нитей.
Несущая нить
Hn = (g + p + Δq) l2 / (8fn) = (1,56 + 4,8 + 0,1) · 652 / (8 · 3) = 1137 кН.
Требуемая площадь сечения каната двойной свивки ЛК-РО при нормативном сопротивлении проволок Run = 156,8 кН/см2
An = 1,6Hn / kp Run = 1,6 · 1137 / (0,75 · 156,8) = 15,47 см2 = 1547 мм2.
Назначаем (табл. П8.1) канат диаметром 61,5 мм с площадью сечения An = 1782,25 мм2. Модуль упругости (табл. 8.4) E = 1,5 · 104 Н/см2.
Стабилизирующая нить
Hs = q0l2 / (8fs) = 0,5 · 652 / (8 · 2) = 132 кН.
Требуемая площадь поперечного сечения спирального каната ЛК-Р при Run = 137,2 кН/см2
As = 1,6 · 132 / (0,81 · 137,2) = 1,9 см2 = 190 мм2.
Назначаем канат диаметром 20,5 мм, для которого А = 192,11 см2; E = 1,5 · 105 кН/см2.
Для уточнения коэффициента а предварительно находим отношение длин нитей к пролету

Коэффициент α по формуле (8.72) равен
394
α =
=
| 1,00572 · 1,9 · 10-4 · 2 |
| 1,00252 · 15,47 · 10-4 · 3 |
= 0,0824.
Уточняем значения контактных нагрузок
q = (1,56 + 4,8)
= 0331 кН/м; Δq = 0,25 · 0,331 = 0,083 кН/м;
q0 = 0,331 + 0,083 = 0,414 кН/м.
Производим повторный подбор сечений нитей.
Расчет несущей нити: Hn = 1134 кН; Vn = 209,4 кН; Тn = 1153,2 кН: Аn = 1570 мм2. Назначаем канат ЛК-РО конструкции 6×36 диаметром 61,5 мм с временным сопротивлением проволок 156,8 кН/см2 (Аn = 1782,55 мм2).
Расчет стабилизирующей нити: Hs = 109,3 кН; Vs = 13,46 кН; Ts = 110,13 кН; As = 158,6 мм2. Назначаем спиральный канат ЛК-Р конструкции 6x19 диаметром 19 мм с временным сопротивлением проволок 137,2 см2. (А = 165,68 см2).
Для оценки деформативности покрытия находим дополнительную стрелку провеса в середине пролета от нормативной снеговой нагрузки
Δfi = k
| pil4 |
| (1 + αfs / fn) EAnfn2 |
=
| (1 · 10-4 · 300) · 65004 |
| (1 + 0,824 · 2,00 / 300) 15 · 103 · 17,8 · 3002 |
= 49,51 см > (1/200) l = 32,5 см.
Покрытие не удовлетворяет условию жесткости, а это может привести к снижению его долговечности.
Увеличим контактную нагрузку до q0 = 0,7 кН/м2. Падение контактной нагрузки при загружении покрытия постоянной нагрузкой и снегом сохранит прежнее значение, поэтому остаточная контактная нагрузка будет равна Δq = 0,7 - 0,4 = 0,3 кН/м2. Повторяя подбор сечений нитей при новом значении q0, и, следовательно, распоров, обратите внимание, что предпочтение нужно отдавать канатам с небольшими значениями временного сопротивления проволок разрыву. Это связано с тем, что жесткость системы зависит от площади сечения канатов и не зависит от их прочности. Поэтому условие прочности канатов (1,6T/A, kp Ru, n) следует обеспечить путем увеличения их диаметров при одновременном снижении предела прочности проволок.
Выбирая Ry,n = 117,6 кН/см2 и повторяя расчет, назначаем канаты: для несущей нити - ЛК-РО диаметром 72 мм (Аn = 23,16 см2); для стабилизирующей нити - ЛК-Р диаметром 27 мм (As 3,38 см2).
Дополнительная стрелка провеса в середине пролета от нормативной снеговой нагрузки будет равна 37,4 см. Таким образом, мы существенно уменьшили деформативность покрытия, но не получили желаемого результата, так как новое значение стрелки превышает нормируемую величину 32,5 см.
Увеличим начальную стрелку несущей нити до 3,3 м. Тогда:
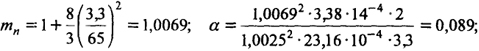 Δf =
Δf =
| 3 · 3 · 654 |
| 128 (1 + 0,089 · 2/3,3) 15000 · 104 · 23,16 · 10-4 · 3,32 |
= 0,315 < 0,325 м.
Условие жесткости обеспечено. Формально далее нужно повторить расчет и оценить прочность канатов при новом значении стрелки провеса несущей нити. Мы не будем этого делать, полагая, что увеличение стрелки на 10% приведет к запасу прочности несущей нити
395
в таких же пределах. Вы можете поступить иначе и не исключено, что сумеете принять канат меньшего диаметра. Но в этом случае не забудьте еще раз проверить деформативность, т.к. при меньшем диаметре каната она станет несколько большей.
Определим длины исходных заготовок для нитей, для чего предварительно вычислим распоры в нитях от контактной нагрузки:
Нn = q0 l2 / (8fn) = 0,414 · 652 / (8 · 3) = 72,88 кН;
Hs = q0 l2 / (8fs) = 0,414 · 652 / (8 · 2) = 109,32 кН.
Искомые длины исходных заготовок будут равны:
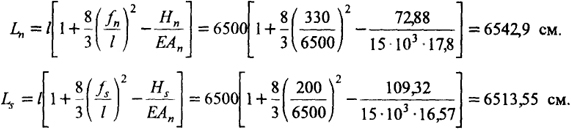
Подбор сечения распорок.
Сжимающее усилие при шаге распорок 3 м
N = (q + p + Δq)a = (1,56 + 4,8 + 0,3)3 = 19,98 кН.
Назначаем сечение распорки по предельной гибкости llim = 150. Требуемый радиус инерции сечения i = l0 / llim = 500 / 150 = 3,33 см. По сортаменту (табл. П11.12 [1]) выбираем гнуто-сварной замкнутый профиль 100×100×3 / ТУ 36-2287-80 (A = 11,64 см2; i = 3,96 см). Проверяем устойчивость распорки
λ = 500/3,96 = 126,26; φ = 0,39; N/(φA) = 19,98/(0,39·11,64) = 4,4 < Ryγс.
396
1
Приведенный здесь расчет ориентирован на случай предварительного напряжения системы до приложения постоянной нагрузки при условии, что ветровой отсос меньше постоянной нагрузки. В противном случае к контактной нагрузке
q0 нужно добавить разницу между ветровым отсосом и постоянной нагрузкой.
