| 8f. Высоту стенки таких нитей назначают в пределах h = (1/60...1/90) пролета, если сечение сплошное и h = ( 1/25...1/40) пролета при сквозных сечениях.
Если нить выполнена в виде фермы или балки параболического очертания, то ее при расчете разбивают на отдельные участки. Дифференциальное уравнение оси нити на каждом участке, имеющее вид
EIy''(x) - Hy0(x) - Hy(x) = M(x),
(8.64)
решают совместно с уравнением зависимости между распором и прогибом
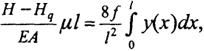(8.65)
где
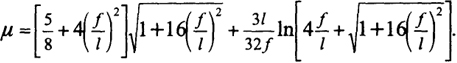
Для определения компоновочных параметров нити задаются стрелой провеса f и высотой сечения нити. Деформации и перемещения нити при загружении ее временной нагрузкой по всему пролету невелики, поэтому наибольшее растягивающее усилие и площадь сечения можно определить по формулам:
(8.66)
Жесткость нити и необходимый момент инерции определяют по формуле (8.60) при загружении половины пролета временной нагрузкой с учетом допускаемых прогибов в четверти пролета. Скомпоновав сечение нити, необходимо выполнить его проверку. Для этого определяют приращение стрелы провеса Δf в середине пролета [формула (8.61)], напряжения изгиба и растяжения:
382
σi =
;
(8.67)
σr =
-
.
(8.68)
Пример 8.4. Нить пролетом l = 65 м загружена постоянной нагрузкой q = 12 кН/м и временной нагрузкой p = 8 кН/м. Стрела провеса нити f = 3,20 м, расчетное сопротивление материала Ry = 24 кН/см2.
Высота сечения нити h = (1/50...1/90)65 = 0,7 см.
Площадь сечения нити
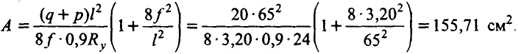
Жесткость нити и ее момент инерции, которые обеспечивают необходимые прогибы [Δf] =
l от действия временной нагрузки на половине пролета, равны:
EI =
;
I =
| 5 · 8 · 654 · 108 · 200 |
| 384 · 100 · 32 · 2,06 · 104 · 65 · 102 |
= 86792 см4.
Принимаем сечение нити из двутавра с площадью А = 164,7 см2 и моментом инерции I = 125930 см4. Увеличение стрелы провеса:
Äf =
| 3 · 8 · 654 · 108 · 1,013 |
| 128 · 2,06 · 104 · 164,7 · 3,22 · 104 · 102 |
= 9,92 см.
Напряжения изгиба и растяжения (8.67), (8.68):
σi = y''E
=
| 9,92 · 192 · 70 · 2,06 · 104 |
| 20 · 652 · 104 · 2 |
= 1,62 кН/см2;
σr =
| 20 · 652 |
| 8 · (3,2 + 0,092) ̭ 164,7 |
-
| 48 · 2,06 · 104 · 125930 · 9,92 |
| 5(3,2 + 0,092) 652 · 104 · 164,7 · 107 |
= 19 39 кН/см2;
σ = σr + σi = 19,39 + 1,62 = 21,01 кН/см2 < 0,9 · 24 = 21,6 кН/см2.
Точные расчеты конструкций с нитями конечной изгибной жесткости приводятся в литературе [8, 17, 19].
383
|
 |
