Эти нити обычно имеют сплошное сечение высотой h = (1/200...1/350) пролета, выполненное из прокатных профилей. Дифференциальное уравнение оси нити имеет вид:
ЕIу''(x) - Ну(х) = М(х),
(8.51)
где М(х) - момент от поперечной нагрузки (балочный момент).
Распор, напряжения растяжения σr и изгиба σi в нити определяют по следующим формулам:
H =
;
(8.52)
σr =
=
-
;
(8.53)
σi =
=
=
,
(8.54)
378
где Мт - изгибающий момент в нити, А и h - площадь и высота сечения нити.
Аппроксимируя уравнение оси нити балочной функцией
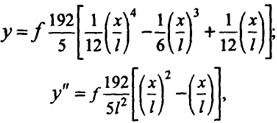(8.55)
где f - стрела провеса нити в середине пролета, можно определить распор, изгибающий момент и напряжения в середине пролета нити. При заданной высоте сечения h и стреле провеса для нити, загруженной равномерно распределенной нагрузкой, будем иметь:
H =
-
; M = EIy'' = EIf
;
σr =
-
; σi =
; σ = σr + σi.
(8.56)
Дополнительная нагрузка вызывает перемещение нити, изменяет усилия в ней и возникает необходимость в совместном решении системы уравнений. В эту систему входят дифференциальное уравнение оси нити, загруженной постоянной нагрузкой (8.51), уравнение нити, загруженной полной расчетной нагрузкой, и зависимость между распорами и прогибами.
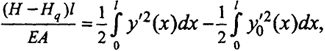(8.57)
где H, Hq - распор от полной и постоянной нагрузок, у0(х) и у(х) - уравнения оси нити, загруженной постоянной и полной нагрузками.
Для определения компоновочных параметров нити задаемся рекомендуемой стрелой провеса f и высотой сечения нити h. Загружаем нить равномерной постоянной нагрузкой q, временной р по всему пролету и находим напряжения изгиба в середине пролета
σu = y''
E =
=
.
(8.58)
Из формулы (8.56), пренебрегая вторым членом, определим площадь сечения нити:
379
A =
.
(8.59)
Жесткость нити определим из допускаемых перемещений в четверти пролета. Предполагая дополнительные прогибы нити, загруженной временной нагрузкой на половине пролета подобными перемещению балки с пролетом 0,5l, найдем жесткость нити
[Δf] =
=
,
откуда
EI =
,
где Δf - допускаемый прогиб в четверти пролета нити;
I =
.
(8.60)
Требуемые площадь сечения и момент инерции позволяют подобрать необходимый профиль по сортаменту.
Пример 8.2. Нить пролетом l = 65 м загружена постоянной нагрузкой q = 3,5 кН/м и временной p = 1,5 кН/м. Расчетное сопротивление материала нити Ry = 36,5 кН/см2. Задаемся стрелой провеса нити и высотой ее сечения
f =
l =
65 = 3,25 м; h ≈
l ≈
6500 = 20 см .
Найдем напряжение изгиба
σu =
=
| 24 · 325 · 2,06 ?#183; 104 · 20 |
| 5 · 65 · 104 |
= 15,21 кН/см2.
Площадь сечения нити
A =
=
= 38,14 см2.
Определим жесткость нити из условия загружения покрытия временной нагрузкой на половине пролета
EI =
| 5 · 0,5P (0,5l)4 |
| 384EI[Δf] |
=
.
Допускаемый прогиб в четверти пролета
Δf =
l =
65 = 0,325 м;
EI =
| 5 · 1,5 · 654 · 108 |
| 384 · 100 · 32 · 32,5 |
= 44,68 · 106 кН·см;
380
I =
=
= 2169 см4.
Принимаем нить из двутавра № 20 с площадью сечения A = 38,95 см2 и моментом инерции I = 2660 см4.
Для определения напряженного состояния нити необходимо уточнить стрелу провеса. Приближенно величина прогиба при равномерной нагрузке по всему пролету
Δf =
,
(8.61)
где μ ≈ 1 +
(
) = 1,0066; μ
2 = 1,0132;
Δf =
| 3 · 1,5 · 654 · 108 · 1,0132 |
| 128 · 100 · 2,06 · 104 · 38,95 · 3,252 · 104 |
= 7,3 см;
σr =
-
=
| 5 · 652 |
| 8(3,25 + 0,073) 38,95 |
-
| 48 · 2,06 · 104 · 2660 |
| 5 · 652 · 104 · 38,95 |
= 20,1 кН/см2;
σi =
=
| 48 · 2,06 · 104 · 332 · 20 |
| 10 · 652 · 104 |
= 15,54 кН/см2;
σ = σr + σi = 20,1 + 15,54 = 35,64 кН/см2.
При известных параметрах поперечного сечения нити можно определить стрелу провеса, обеспечивающую минимальные напряжения в несущих элементах.
Полные напряжения в нити по формулам (8.56) равны
σ =
-
+
.
Приравнивая производную
нулю
, получим
f = √
.
(8.62)
Пример 8.3. Определим оптимальную стрелу провеса для нити, выполненной из двутавра № 20. Площадь сечения A = 38,95 см2, высота сечения h = 20 см, пролет l = 65 м, нагрузка по всему пролету q = 5кН/м:
f = √
| 5 · 5 · 64 · 108 |
| 192 · 2,06 · 104 · 38,95 · 20 |
= 380,578 см.
Напряжения в нити в этом случае будут равны
σi = 17,8 кН/см2; σr = 17,5 кН/см2; σ = 35,31 кН/см2.
381
