Гибкие нити висячих покрытий, как правило, проектируют со стрелками провисания 1/10... 1/30 от пролета. Такие нити называют пологими и принимают нагрузку распределенной не по длине нити, а по пролету. Расчетная схема нити показана на рис.8.16. Нормальную силу T называют тяжением, а его горизонтальную составляющую H-распором. Вертикальные составляющие тяжения на опорах можно определить из уравнений равновесия, приравнивая нулю моменты в опорных шарнирах. Проделав это, можно убедиться, что вертикальные составляющие равны реакциям в простой балке, загруженной той же что и нить нагрузкой, поэтому их называют балочными реакциями.
При записи выражения для изгибающего момента в произвольной точке нити С можно заметить, что этот момент отличается от балочного момента М(х) наличием дополнительного члена Ну(х). Поскольку нить не способна работать на изгиб, изгибающий момент в любой точке нити равен нулю, поэтому
М(х) - Ну(х) = 0; или Н =
; y(x) =
,
(8.3)
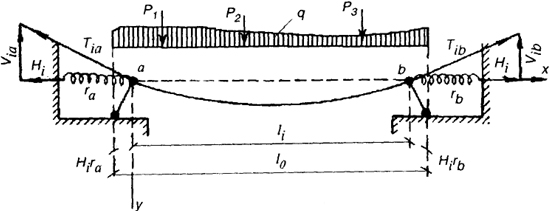 Рис. 8.16. Расчетная схема нити
Рис. 8.16. Расчетная схема нити
353
где М(х) - балочный момент, т.е. изгибающий момент в сечении с координатой x шарнирно опертой балки при той же нагрузке.
Дифференцируя последнее выражение в (8.3), найдем
=
=
.
(8.4)
Длину кривой S с известным математическим выражением у(х) можно определить путем суммирования элементарных отрезков ds, составляющих эту кривую:
 (8.5)
(8.5)
Подставляя значение dy/dx из (8.4), раскладывая подкоренное выражение в ряд и удерживая два первых его члена, можем записать:

ИЛИ
S = l +
,
(8.6)
где принято обозначение
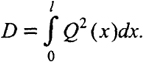 (8.7)
(8.7)
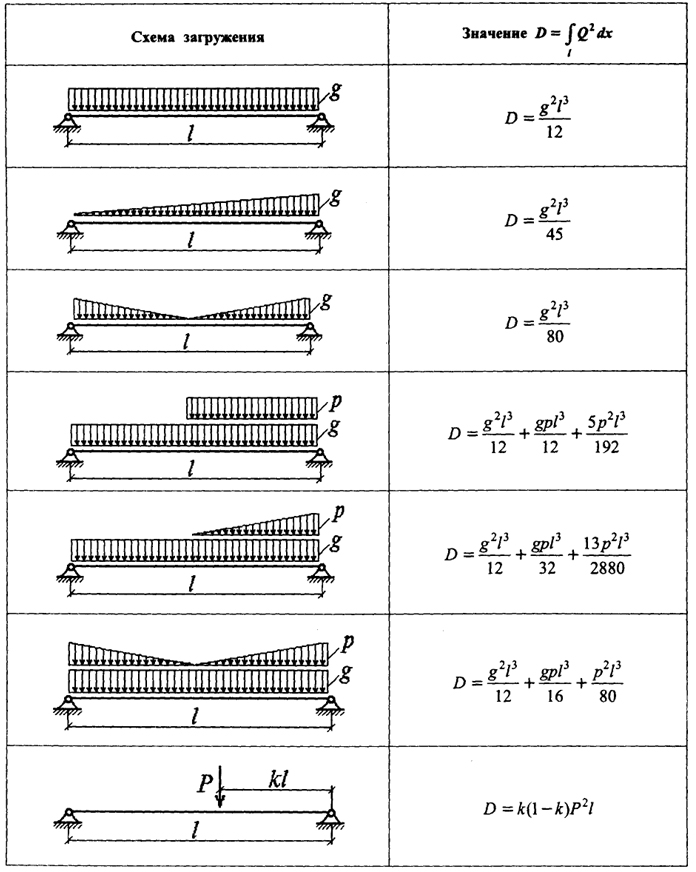
Последнюю формулу вы будете часто использовать при расчете нитей. Значение D можно определять непосредственным интегрированием или по способу Верещагина путем "перемножения" самой на себя эпюры поперечных сил. В табл. 8.3 даны готовые формулы вычисления D для наиболее характерных схем нагрузок.
Обратите внимание на одну особенность расчета гибкой нити. Для того чтобы определить тяжение нити, нужно знать стрелку провеса в расчетном состоянии. Эту стрелку конструктор может задать по своему усмотрению, но для этого нужно знать стрелку в период монтажа, которая вследствие изменившихся условий (нагрузок, температуры, перемещения опор и др.) будет иной. Другими словами, необходимо связать два состояния нити: исходное (монтажное) и расчетное. Задав произвольную стрелку в одном из этих состояний, следует найти вполне определенное значение стрелки в другом состоянии, изменившееся за счет упругих и кинематических перемещений.
354
Таблица 8.3. Значения параметра D
Итак, рассмотрим два состояния нити: исходное, характеристики которого будем снабжать индексом 0, и некоторое опасное для нити состояние, подлежащее проверке, которое будем называть расчетным и снабжать связанные с ним обозначения индексом i.
355
В исходном состоянии длина нити по (8.5) равна
S0 = l0 +
.
(8.8)
Для расчетного i-го состояния будем иметь
Si = li +
.
(8.9)
При переходе из исходного состояния в расчетное, например в связи с увеличением нагрузки, нить будет растягиваться и ее длина изменится в соответствии с законом Гука на величину
Si - S0 =
.
(8.10)
Тяжение переменно по длине нити, поэтому будем использовать усредненное значение
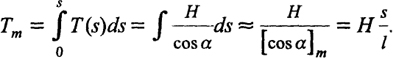 (8.11)
(8.11)
С учетом этого равенства и зависимостей (8.8), (8.9) выражение (8.10) примет вид
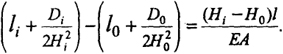 (8.12)
(8.12)
Если опоры не смещаемы, то пролеты li = l0 = l; в этом случае формулу (8.12) можно преобразовать к виду:
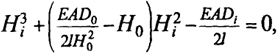 (8.13)
(8.13)
где Е - модуль упругости нити; А - площадь ее поперечного сечения.
Кубическое уравнение (8.13), связывающее два состояния нити, будем в дальнейшем называть уравнением состояний.
Если в исходном состоянии нить загружена только собственным весом, то распор Н0 (второй член в скобках) уравнения (8.13) можно полагать равным нулю, однако для раскрытия неопределенности первый член в скобках необходимо учитывать. В случае, когда состояние i отличается от состояния 0 только интенсивностью нагрузки, выражение в скобках будет равно:
EAD0 / 2lH02 = EA(q02l3 / 12) / 2l(q0l2 I 8) = (8EAf02) / (3l2).
356
С помощью уравнения состояний (8.13) задача расчета гибкой пологой нити становится полностью решенной.
• Зная нагрузку в исходном (например, монтажном) состоянии и задав стрелку провисания нити f0, можно найти по формуле (8.3) распор нити в этом состоянии
H0 = H0,max / f0.
• По формулам табл. 8.3 [или непосредственно по формуле (8.7)] вычисляют параметры D0 и Di соответственно для нагрузок исходного и расчетного состояний, затем записывают и решают кубическое уравнение (8.13) и находят тем самым распор в расчетном состоянии.
• Определяют балочную реакцию от нагрузки расчетного состояния, вычисляют тяжение Ti = √Vi2 + Hi2 и проверяют прочность нити. Т ≤ ARyγc. Любопытства ради можно найти стрелку провеса при действии расчетной нагрузки fi = Mi,max / Hi.
• Если нет полной уверенности в том, что выбранное расчетное состояние является самым опасным для нити, то следует проверить другие состояния, всякий раз повторяя перечисленные операции.
Обратите внимание: все сказанное можно сделать, если известна площадь сечения нити А, иначе не удастся решить уравнение (8.13). Этой площадью следует задаться на основании тех или иных соображений, например заимствовать ее из аналогичного проекта. Если таких соображений и аналога нет, то можно выполнить предварительный расчет, сделав все, что было сказано, наоборот.
Задайте стрелку провеса в состоянии нити, которое вы считаете наиболее опасным, ориентируясь на прежнее соотношение fi = (1/10...1/30)l. Найдите распор Hi = Mmax / fi, вертикальную реакцию в этом состоянии Vi и тяжение нити Ti = √Vi2 + Hi2. Из условия прочности назначьте площадь сечения нити A = Ti / Ryγc. Теперь запишите уравнение состояния (8.13) наоборот, поменяв индексы (вместо i пишите 0, а вместо 0 - i). Найдите корень кубического уравнения, т.е. распор H0, а затем вычислите искомую стрелку f0 = М0/Н0 в исходном состоянии нити. Далее можно проверить остальные опасные загружения нити.
Для того чтобы реализовать исходную стрелку в натуре при монтаже конструкций, следует знать длину исходной заготовки L. Эту длину нетрудно определить по формуле (8.8) за вычетом упругого удлинения нити (8.10), которое для пологих нитей приближенно можно определить по формуле ΔS = Н0l / ЕА. Применительно к равномерно-распределенной нагрузке будем иметь
357
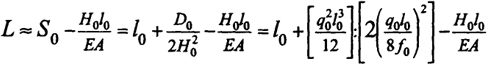
или
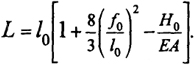 (8.14)
(8.14)
Эта формула записана применительно к исходному состоянию, но ее можно использовать для i-го состояния.
Обратите внимание на необходимость не только обеспечить прочность нити, но и ограничить ее перемещения от временной нагрузки с тем, чтобы не допустить повреждений ограждающих конструкций, в том числе гидроизоляционного ковра. Вот почему все полученные выше зависимости имеют практический смысл лишь при наличии дополнительных ограничений на деформативность нити. Такие ограничения нетрудно получить, повторив преобразования, аналогичные (8.8) - (8.12). При этом за исходное состояние нити следует принять ее загружение постоянной нагрузкой при стрелке f0 и распоре H0, а дополнительному загружению нити нормативной временной нагрузкой рn будут соответствовать стрелка и распор, равные f1 и Н1. В результате будет получена следующая формула для вычисления упругого дополнительного провеса нити в середине пролета при действии равномерно-распределенных нагрузок:
 (8.15)
(8.15)
где рn - временная нормативная нагрузка на 1 м пролета нити; l - пролет нити; Δf - стрелка предельного дополнительного провеса неомоноличенного покрытия от временной нагрузки, которую можно принять (1/200...1/300) l при последующем омоноличивании конструкции; L - длина исходной нити, определяемая по формуле (8.14).
Понятно, что после расчета нити по условию прочности в указанной выше последовательности нужно проверить выполнение условия (8.15). Но можно поступить иначе. Находим требуемую площадь сечения нити А по формуле (8.15), а затем проверяем ее прочность. Для этого можно воспользоваться формулой [9]
 (8.16)
(8.16)
358
где q и р - расчетные постоянные и временная нагрузки на 1 м пролета нити; Ry - расчетное сопротивление нити.
Распор струны. Нить первоначально прямолинейную, имеющую начальную длину, не превышающую пролета, натянутую силой N и работающую на поперечную нагрузку, называют струной. При нагружении струны поперечной нагрузкой продольная сила в ней возрастает и распор на основании (8.13) может быть определен из выражения
H3 - NH2 -
= 0.
(8.17)
Нить с опорами в разных уровнях. Конфигурацию нити с опорами в разных уровнях можно дополнить до нити с опорами на одном уровне. По сути дела в расчете нити ничего не меняется, за исключением различий величин тяжений нити на опорах А и В, что является следствием различий вертикальных составляющих тяжений, которые будут равны:
Va = Va,bim + Н · tg β; Vb = Vb,bim - H · tg β,
(8.18)
где Vbim - балочные реакции; β - угол наклона к горизонтали хорды, стягивающей опоры нити.
Уравнение состояний в общем случае. При выводе уравнения состояний (8.13) мы рассматривали нить с опорами в одном уровне, не учитывали их возможную податливость, не принимали во внимание различие температур окружающей среды в исходном и расчетном состояниях. Для учета этих факторов следует ввести поправки на их влияние. Для учета податливости опор нужно ввести поправку на изменение пролета в уравнение (8.12), а температурные изменения длины нити можно отразить в левой части равенства (8.10).
В.К. Качурин получил обобщенное уравнение состояний нити, в котором учтены все отмеченные обстоятельства:
H3 + aH2 - b = 0,
(8.19)
где a =
-
H0 +
| v sin β cos2 β + u cos2 β + αlt cos β |
| l |
EA;
b =
.
Здесь β - угол наклона к горизонтали хорды, стягивающей опоры нити; αtl - температурное удлинение нити; u, v - горизонтальная и вертикальная составляющие принудительного перемещения одной из опор относительно
359
другой. Для учета упругой податливости опор в знаменателях коэффициентов а и b вместо пролета l следует подставить lef = (1 + nЕА · cos3 b), где v = va + vb - упругая податливость опор от ΔH = 1 (определение D0, Di, Н0 при этом ведется по размеру пролета l).
Стрелку провеса нити w = w(х) в сечении х можно определить из кубического уравнения
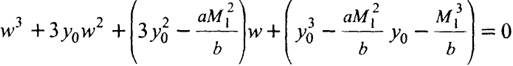 (8.20)
(8.20)
или приближенно по формуле
 (8.21)
(8.21)
где y0 = y0(х) - начальная ордината провеса нити в сечении x; M1 = Мbim(х) - балочный момент в сечении x при i-м состоянии нити; а и b - коэффициенты в формуле (8.19).
360
