Рассмотрим для определенности пластину, свободно опертую по контуру под действием нагрузки, равномерно распределенной по всей поверхности (рис. 7.19).
Расчетные формулы для такой пластины имеют вид [13]:
323
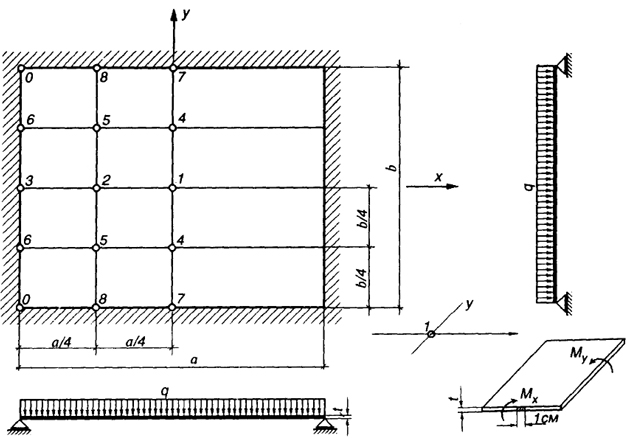Рис. 7.19. Расчетная схема пластины с указанием точек, соответствующих данным таблиц 7.1...7.3
- прогиб пластины в центре: w = α1
;(7.2)
- изгибающие моменты: Мх = α2qa2; Му = α3qа2;(7.3)
- поперечная сила: Q = α4qa;(7.4)
- опорные реакции на единицу длины опорных кромок:
V = α5qa; V0 = α6qab.
(7.5)
Индексы при моментах означают направление, перпендикулярное соответствующей оси; V0 - реакции, сосредоточенные в вершинах прямоугольного опорного контура пластины.
Значения коэффициентов α1...α6 в зависимости от соотношения сторон b/а приведены в табл. 7.1...7.3 для указанных на рис. 7.19 точек пластины (при v= 1/6).
Цилиндрическая жесткость плиты D =
в первом приближении может быть определена, как для пластины с такой толщиной, чтобы она оказалась эквивалентной по изгибной жесткости полоске единичной ширины, вырезанной из структурной плиты. Практически это можно сделать
324
Таблица 7.1. Значения коэффициента α1 в формуле (7.2)
Таблица 7.2. Значения коэффициентов α2 и α3 в формуле (7.3)
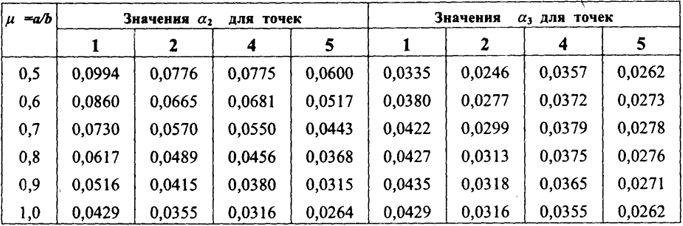
Таблица 7.3. Значения коэффициентов α4, α5, α6 в формулах (7.4) и (7.5)
так: определить приближенно момент инерции поясных сеток (по ширине ячейки) и разделить на ширину ячейки. Предположим, что пояса ортогональной структуры расположены с шагом s - 3 м. Момент инерции структуры для полоски шириной 3 м определим по формуле:
Jx = 0,9
h2,
(7.6)
где A1, А2 - площади сечения стержней верхней и нижней сеток; h - высота (толщина) структурной плиты.
325
Значение этого момента инерции, деленное на 300 см, и даст величину момента инерции J для полоски из плиты единичной ширины ( 1 см ). Эквивалентная толщина плиты, таким образом, равна t = 3√12J.
Таким образом, приближенное общее выражение для эквивалентной цилиндрической жесткости ортогональной структурной плиты может быть записано в виде:
D =
| 0,9EA1A2h2 |
| b(A1 + A2)(1- v2) |
,
(7.7)
где b - ширина ячейки структуры, см.
Для некоторых типов структур известны и более точные выражения для упругих характеристик [8], [9]. Так, для ортогональной системы с перекрестным расположением диагоналей в обеих поясных сетках при однородных упругих свойствах верхней и нижней сеток цилиндрическую жесткость плиты определяют выражением:
D = Dx = Dy =
,
(7.8)
где А1 - площадь сечения стержня верхнего пояса; α - угол наклона раскосов, соединяющих пояса, к вертикали; п - соотношение площадей сечения поясов A1/A2.
Модули упругости плиты относительно главных осей и коэффициент Пуассона при этом находят по формулам:
Ex = Ey =
(1 + v), v =
,
(7.9)
где Af - площадь сечения пояса; m = Af / Ad, Ad - площадь сечения диагонали в сетке.
При значительном отличии коэффициента Пуассона от табличного (напомним, что в табл. 7.1...7.3 vt = 1/6) для уточнения значений изгибающих моментов можно воспользоваться приближенной формулой [12]:
М1 =
[(1 - vvt) Mit + (v - vt) M2t],
(7.10)
где M2 = My, если M1 = Мх и М2 = Мх, если М1 = Му; Mit - значение момента, определенное с помощью таблицы.
Регулярная система с квадратной ячейкой и диагоналями малого сечения (Ad → 0; m → ∞) превращается в систему, не воспринимающую кручения, близкую к обычным перекрестным фермам, у которой жесткость
326
на кручение Dt = 0 и v = 0. Цилиндрическую жесткость плиты в этом случае определяют по формуле:
D =
.
(7.11)
При
т → ∞ (
Af → 0, т.е. поясные сетки вырождаются) система приближается к перекрестным фермам, развернутым под углом 45° к осям
х и
у, для которой
v = 1, а цилиндрическая жесткость плиты
D = Dt =
,
(7.12)
где A1d - площадь сечения верхней диагонали; п - соотношение площадей верхней и нижней диагоналей.
При необходимости приближенного расчета структурных плит с другими вариантами кристаллического строения вам придется обратиться к специальной литературе, например [8], [9].
327
