Сетчатые купола обычно рассчитывают на прочность при упругих деформациях с последующей проверкой устойчивости конструкции.
Пренебрегая перераспределением усилий в элементах конструкции, которые могут возникать вследствие возможных неупругих деформаций, пользуясь данными, полученными из упругого расчета, можно подобрать сечения элементов и проверить прочность конструкции.
Известны два основных подхода к расчету сетчатых куполов:
- Сетчатый купол рассматривают, как сплошную осесимметричную оболочку, поскольку он имеет сходство со сплошной оболочкой. На основании этого заменяют сетчатую конструкцию сплошной оболочкой, проводят расчет по безмоментной теории и затем осуществляют обратный переход к усилиям в дискретной системе. При этом определяют жесткостные свойства эквивалентной сплошной оболочки, имеющей ту же прочность на растяжение, изгиб и кручение, что и заданная сетчатая система. Перемещения точек сплошной оболочки совпадают с перемещениями ее узлов. Переход от полученных напряжений в сплошной оболочке к усилиям в стержневой сетчатой системе основывается на условиях статического равновесия.
- Сетчатый купол рассматривают как дискретную стержневую систему и рассчитывают известными методами строительной механики пространственных стержневых систем. Этот подход реализуют с помощью ПЭВМ и использованием программ статического расчета пространственных систем, таких, как "Лира", "Спринт", "Парсек", "Scad" и др.
Более подробно рассмотрим первый подход, для чего воспользуемся безмоментной теорией расчета применительно к сферическим куполам-оболочкам. При действии на конструкцию осесимметричной нагрузки основное уравнение напряженного состояния, согласно указанной теории, имеет вид
Т1 + Т2 = - qR,
(6.14)
где Т1 - меридиональное усилие на единицу длины кольцевого сечения; Т2 - кольцевое усилие на единицу длины дуги меридиана; q - равномерно распределенное нормальное к поверхности купола давление, направленное к центру сферы; R - радиус сферического купола.
290
Определение усилий от собственного веса. Постоянную нагрузку от собственного веса g считают равномерно распределенной по всей поверхности купола (рис. 6.19, а). Для определения меридионального усилия Т1 рассмотрим равновесие верхней части купола, отсеченной горизонтальной плоскостью, проходящей на расстоянии у от центра сферы (рис. 6.19, а). На отсеченный сферический сегмент действует нагрузка от собственного веса вышележащей части купола
2πrfg = 2πr(R - Rcosφ)g ,
(6.15)
которая уравновешивается проекцией на вертикальную ось меридиональных усилий Т1, действующих по периметру кольцевого сечения радиусом r = Rsinφ,
Т1 2πr · sinφ = T1 2πR · sin2φ,
(6.16)
отсюда меридиональное усилие на единицу длины кольца равно
T1 = -
= -g
.
(6.17)
Кольцевое усилие Т2 найдем из основного уравнения безмоментной сферической оболочки (6.14), выражая давление g через вертикальную нагрузку q, а Т1 через значение уравнения (6.17) q = gcosφ,
-g
+ T2 = -g cosφ · R,
(6.18)
откуда кольцевое усилие на единицу длины меридиана
 (6.19)
(6.19)
При угле φ = 51°49' кольцевое усилие меняет свой знак, переходя от сжимающего к растягивающему.
Усилия Т1 и Т2, определенные по формулам (6.17) и (6.19), справедливы для сплошного замкнутого купола. Если в куполе имеется фонарное отверстие и масса фонаря более чем в 1,5 раза отличается от массы вырезанной части купола, то необходимо учесть распределенную по линии контакта с фонарем нагрузку pk (рис. 6.19, а)
T1= pk (sinφ1 / sin2φ); T2 = pk (sinφ1 / sin2φ).
(6.20)
Растягивающие усилия в опорном кольце от собственного веса купола можно определить по формуле
291
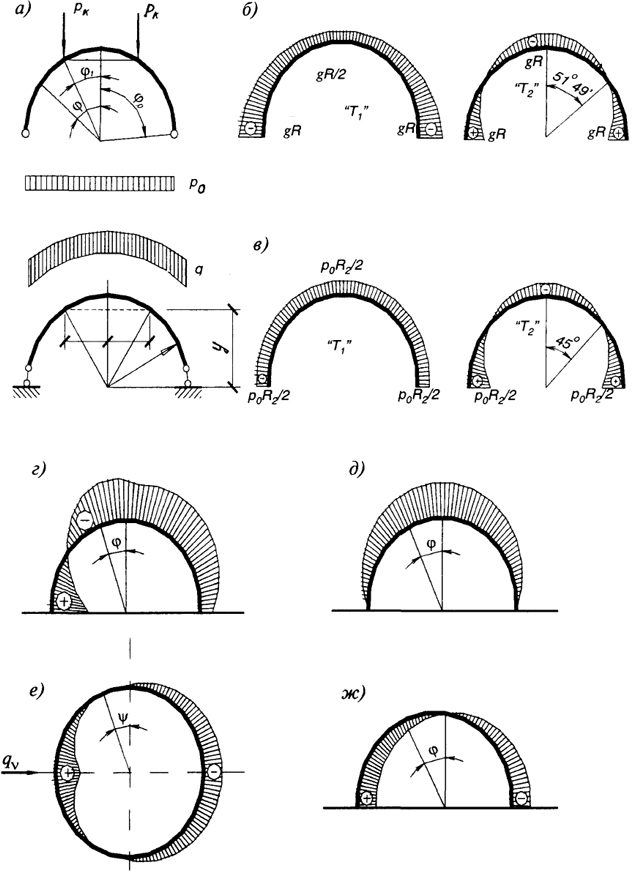 Рис. 6.19. Нагрузки и усилия в куполе-оболочке:а - расчетная схема; б - эпюры меридиональных и кольцевых усилий от собственного веса купола; в - то же, от снеговой нагрузки; г, е - эпюры ветрового давления на угол в поперечном сечении и в плане; д, ж - симметричная и кососимметричная эпюры ветрового давления на купол
Рис. 6.19. Нагрузки и усилия в куполе-оболочке:а - расчетная схема; б - эпюры меридиональных и кольцевых усилий от собственного веса купола; в - то же, от снеговой нагрузки; г, е - эпюры ветрового давления на угол в поперечном сечении и в плане; д, ж - симметричная и кососимметричная эпюры ветрового давления на купол
292
Nk = R2g (1 - cosφ0) / tgφ0 .
(6.21)
При наличии кольцевой нагрузки по фонарному вырезу к указанному усилию следует добавить
ΔNk = pkRsinφ1 ctgφ0 .
(6.22)
Определение усилий от снеговой нагрузки. Интенсивность снеговой нагрузки по поверхности купола обычно принимают по закону косинуса р = р0 cos φ, где p0 - равномерно распределенная нагрузка по проекции поверхности на горизонтальную плоскость.
Меридиональное усилие на единицу длины кольца в любом сечении имеет постоянное значение
T1 = -πr2р0 / 2πrsinφ = -p0R / 2 .
(6.23)
Кольцевое усилие на единицу длины меридиана определится с учетом нормальной составляющей нагрузки в уровне кольцевого сечения q = p0cos2φ из уравнения (6.14)
Т2 = -qR + p0R / 2 = -(1 / 2)p0R cos 2φ.
(6.24)
Кольцевое усилие меняет знак при φ = 45°. Усилие растяжения в опорном кольце
Nk = (p0R2 / 4)sin2φ0.
(6.25)
При действии на купол несимметричной снеговой нагрузки в оболочке кроме меридиональных и кольцевых усилий возникают сдвигающие усилия S. Расчет сферического купола на одностороннюю снеговую нагрузку, исходя из нормальной к поверхности купола нагрузки
p = 0,4p0 (1 + sin φ sin ψ),,
(6.26)
приводит к следующим результатам
 (6.27)
(6.27)
 (6.28)
S =
(6.28)
S =
| (2 + cos φ) (1 - cos φ)2 |
| sin3 φ |
cos ψ,
(6.29)
293
где ψ - угол широты в плане нижнего круга сферического купола (рис. 6.19, е), отсчитываемый от диаметра, перпендикулярного направлению ветра, при котором получается одностороннее загружение.
Определение усилий от ветровой нагрузки. Расчет производят приближенно заменой действительной эпюры ветрового давления (рис. 6.19, г) суммой двух эпюр - симметричной (рис. 6.19, д) qv1 = qv0 cos2 φ, где qv0 - расчетная нагрузка от давления ветра на вертикальную плоскость на уровне основания купола, и кососимметричной (рис. 6.19, ж) qv2 = qv0 sin φ sin ψ.
T1,v = -qv0
| R(1 + cos φ + cos2 φ) |
| 3(1 + cos φ) |
;
(6.30)
 (6.31)
(6.31)
Усилия от кососимметричного загружения ветрового давления:
 (6.32)
(6.32)
 (6.33)
(6.33)
Кососимметричная нагрузка дает сдвигающие усилия, которые можно определить из табл. 6.2.
Купольные покрытия обладают хорошей обтекаемостью, поэтому при f / l ≤ 1 / 4 достаточно учесть только симметричный отсос. Для купола с f / l > 1 / 4 следует принимать во внимание и кососимметричную ветровую нагрузку.
Таблица 6.2. Сдвигающие усилия в сферическом куполе при кососимметричной ветровой нагрузке

294
Проверка устойчивости отдельных элементов купола и сферической оболочки в целом. Усилия сжатия в верхнем кольце купола от суммарного воздействия нагрузки, определяемое по формуле
Nk = T1rkcos φk,
(6.34)
должно быть меньше критического
Nk ≤
,
(6.35)
где Ek, Ik, rk - соответственно модуль упругости материала, момент инерции относительно вертикальной оси и радиус кольца.
Устойчивость сферической оболочки проверяют также по критическим напряжениям
σcr,ob =
≥ σmax,
(6.36)
где tob - толщина оболочки; Еоb, μob - модуль упругости и коэффициент Пуассона материала оболочки; σmах - суммарные сжимающие напряжения от всех видов загружения.
Для сетчатых куполов рекомендуют следующие формулы перехода к сплошному аналогу:
для однослойного купола
Eob = ЕА / 3il; tob = 2i√3; μob = 1 / 3;
(6.37)
для двухслойного купола
Eob = 4EI / 3kl2; tob = ka√3; μob = 1 / 3,
(6.38)
где EI, μ, A, i, l - соответственно изгибная жесткость, коэффициент Пуассона, площадь сечения, радиус инерции и длина стержня сетчатого купола; а - шаг стержней; k - коэффициент, который определяют из условий, что kl соответствует толщине двухслойной оболочке.
Усилия в стержнях купола определяют умножением усилий Т1 и Т2 на соответствующие расстояния между стержнями в рассматриваемом сечении купола и проектированием их на направления стержней (рис. 6.20).
Усилие в стержне меридионального направления
N1 = (T1a) / (2cos α).
(6.39)
Усилие в кольцевом стержне
N2 = T2b.
(6.40)
295
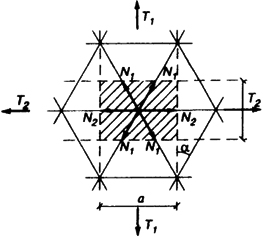 Рис. 6.20. К расчету сетчатого купола
Рис. 6.20. К расчету сетчатого купола
 Рис. 6.21. Расчетная схема купола для определения усилий краевого эффекта:1
Рис. 6.21. Расчетная схема купола для определения усилий краевого эффекта:1 - опорное кольцо;
2 - оболочка купола
Помимо осевых усилий N1 и N2 в стержнях могут возникать изгибающие моменты от местной нагрузки.
Чтобы избежать потери устойчивости в вертикальной плоскости, момент инерции стержней должен удовлетворять условию
I ≥ (T1Ra) / (0,5E) √(T1R) / (0,5E).
(6.41)
Определение краевых усилий в месте сопряжения купола с опорным кольцом. В зависимости от толщины оболочки разделяют на тонкостенные и толстые. Оболочки, для которых справедливо условие tob / r1 ≈ tob / r2 ≤ 1 / 20, считают тонкими. Здесь r1 и r2 - радиусы кривизны в двух взаимно перпендикулярных направлениях.
Купольные покрытия в большей степени соответствуют тонкостенным оболочкам, поэтому в дальнейшем рассмотрим тонкостенные купола-оболочки, для которых справедлива безмоментная теория по всей области оболочки, кроме сравнительно узких зон в месте примыкания оболочки к опорному кольцу. В этих местах свободной деформации оболочки препятствуют опорные закрепления, которые вызывают краевые поперечные силы и изгибающие моменты (краевой эффект). Эти усилия могут быть определены обычными методами строительной механики (рис. 6.21).
Ниже приводится решение такой задачи методом сил [11]
a11M + a12H + a10 = 0;
a21m + a22H + a20 = 0,
(6.42)
где а11 - ЕJk-кратный угол поворота в рассматриваемом сечении от М = 1 по направлению этого момента; а12 - ЕJk - то же, от H = 1 (если этот угол совпадает по направлению с углом поворота, вызванным М = 1 (т.е. а11), то
296
его принимают со знаком плюс, если нет - то со знаком минус); а21 - EJk-кратное перемещение от М = 1; а21 = a12 (правило знаков то же); a22 - ЕJk-кратное перемещение от Н = 1 по направлению силы H; a10 - EJk-кратный угол поворота в этом же сечении, вызванный внешней нагрузкой (знак принимают положительным, если угол поворота совпадает по направлению с а11); a20 - EJk-кратное перемещение, вызванное внешней нагрузкой (знак принимают положительным, если перемещение совпадает по направлению с Н).
Учет краевого эффекта для сферической оболочки характеризуется:
a11 = C + (Jkrc2 sin2 φ0) / Ix;
(6.43)
a12 = (C2 / 2) sin φ0;
a22 = (C3 / 2) sin2 φ0 + (Jkrc2) / Ak sin2 φ0;
(6.45)
C = 0,76 √tobrc,
где Jk - крутильный момент инерции опорного кольца, приходящийся на единицу длины с учетом меридиональных ребер; Ix - момент инерции сечения опорного кольца в вертикальной плоскости.
При действии постоянной нагрузки - собственного веса имеем:
a10 = (C4 g / 2rc) sin φ0;
(6.46)
a20 = (C4 g / 4) [cos φ0 - 1 / (1 + cos φ0)] sin φ0 + (Jk / Ak) grc3 (1 - cos φ0) cosφ0.
(6.47)
При действии снеговой нагрузки:
a10 = (3C4 psin 2φ0) / 8rc;
(6.48)
a20 = (C4 p / 8) sin φ0 cos 2φ0 +[(Jkprc3) / 4Ak] sin 2φ0 sin φ0.
(6.49)
В случае, когда кольцо опирается на специальную кольцевую балку, угол поворота кольца равен нулю и в формуле (6.43) второй член пропадает.
В случае шарнирного опирания купола на кольцо в уравнении (6.42) М = 0, а12 = 0, a10 = 0, и оно приобретает вид
а22Н + а20 = 0,
(6.50)
297
откуда
Н = -a20 / a22.
(6.51)
В общем случае для любой оболочки вращения опорное кольцо воспринимает усилия, передаваемые на него меридиональными усилиями оболочки - горизонтальными проекциями усилий N1, т.е. распор:
qk = N1 cos φ0.
(6.52)
В кольце возникает растягивающее усилие:
Н = qk rс sin φ0 = N1 rc sin φ0 cos φ0 = N1 rc (sin 2φ0) / 2.
(6.53)
Перемещение кольца от усилия Н, увеличенное в EJk раз, определяют при
a20 = (rc sin φ0 = (Jk / 2Ak )N1rc2 sin 2φ0 sin φ0.
(6.54)
В табл. 6.3 приведены значения перемещения кольца а20 для различных загружений сферического купола.
Значения величин а11, а12, а22 для кольца, приведенные в табл. 6.3, остаются верными для любой оболочки вращения.
Определив из уравнения (6.42) значения моментов и кольцевых усилий, можно найти и величины по длине меридиана оболочки по формулам:
Таблица 6.3. Численные значения функций η1 = е-λсоs λ; η2 = e-λsin λ

298
Мλ = Mη1 + (M + CHsin φ)η2;
(6.55)
Nλ = N2 + (2r / C2) [Mη2 - (M + CHsin φ) η1];
(6.56)
η1 = e-λ cos λ; η2 = e-λ sin λ,
где N2 - кольцевое усилие в безмоментной оболочке; Mλ и Nλ - соответственно интенсивности момента и кольцевого усилия в произвольной точке оболочки; М и H - краевые значения момента и распора, полученные из уравнения (6.42), λ = s / С (отсчет s производят по меридиану начиная от края, к которому приложены М и H); r - радиус кривизны срединной поверхности - длина нормали к поверхности до оси вращения (для сферической оболочки r = rс).
Значение функций η1 и η2 приведены в табл. 6.3.
Расчет сетчатого купола как дискретной стержневой системы. Расчет выполняют на ПЭВМ по пространственным расчетным схемам с учетом реального загружения. При этом существует возможность учесть все виды нагрузок: постоянные, технологические, снеговые, ветровые, сейсмические и др., возможен расчет на температурные воздействия.
На первых этапах проектирования сетчатых куполов для предварительной оценки усилий возможно использование приближенных методов. Для сетчатых куполов с ячейками, близкими к равностороннему треугольнику, может быть использован метод, основанный на аналогии регулярных сетчатых поверхностей со сплошными оболочками [9]. Максимальные усилия в стержнях сетчатого сферического купола с треугольными ячейками могут быть определены по формуле
N = kqRl,
(6.57)
где k - коэффициент, определяемый по табл. 6.4 в зависимости от угловой координаты стержня φ, отсчитываемой от вертикальной оси; q - интенсивность расчетной нагрузки.
При рабочем проектировании куполов всех типов обязательной является проверка степени геометрической нелинейности несущей конструкции, выполняемая путем ее расчета по пространственной схеме с учетом упругих перемещений узлов на действие наиболее неблагоприятного сочетания нагрузок. Усилия в элементах каркаса, полученные его расчетом по деформированной схеме, будут превышать усилия линейного расчета. Поэтому необходимо стремиться к тому, чтобы это превышение было меньше 10...15 %. Основным конструктивным приемом, повышающим жесткость конструкции, является изменение высоты сечения элементов.
299
Таблица 6.4. Значения коэффициента k

На начальных стадиях проектирования степень геометрической нелинейности конструкции сетчатого сферического купола может быть оценена соотношением суммарной расчетной нагрузки и верхней критической, вычисляемой по формуле
Fcr = 4,9p
,
(6.58)
где Е - модуль упругости материала; А - площадь сечения стержня (для двухсетчатых куполов суммарная площадь двух поясов); i - радиус инерции в радиальной плоскости; l - средняя длина стержня; R - радиус кривизны поверхности; р - параметр, учитывающий снижение критической нагрузки за счет возможных отклонений формы поверхности от номинальной. Его определяют по графику (рис. 6.22) в зависимости от параметра начального отклонения, вычисляемого по формуле
ζ0 = 0,52δ / β,
(6.59)
где δ - допуск при изготовлении отдельных стержней; β = 1/(2R) - угол наклона стержней к касательной плоскости в узле.
Формула критической силы (6.58) выведена в предположении упругой работы материала конструкции и поэтому не может быть непосредственно использована при проверке общей устойчивости относительно толстостенных стержневых оболочек.
Верхняя критическая нагрузка сетчатого купола, вычисленная по формуле (6.58), должна, как правило, в 5...10 раз превышать осредненную расчетную нагрузку.
Для сетчатого купола с жесткими узлами в радиальной плоскости приближенная методика подбора сечений стержней, обеспечивающая общую устойчивость конструкции, заключается в следующем.
300
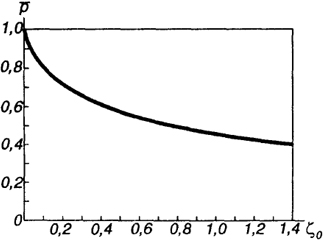 Рис. 6.22. Зависимость параметра верхней критической нагрузки от начальной погиби
Рис. 6.22. Зависимость параметра верхней критической нагрузки от начальной погиби
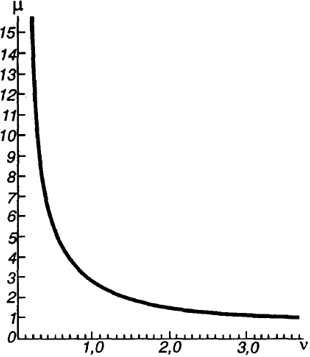 Рис. 6.23. Зависимость коэффициентов свободной длины стержней сетчатого купола μ от параметров условных длину
Рис. 6.23. Зависимость коэффициентов свободной длины стержней сетчатого купола μ от параметров условных длину
Определяют расчетную длину сжатого стержня каркаса
lef = μ l,
(6.60)
где l - геометрическая длина, равная расстоянию между узлами; μ - коэффициент свободной длины, определяемый по графику (рис. 6.23) в зависимости от параметра условной длины стержня
v = l / √Ri.
(6.61)
Проверка несущей способности внецентренно сжатого стержня может быть выполнена в соответствии с нормами [7] на расчетные усилия, полученные из линейного расчета.
При v > 3 коэффициент свободной длины равен единице. Это означает, что при соответствующих соотношениях кривизны поверхности, изгибной жесткости стержня и его длины каждый узел является не упруго-податливой, а абсолютно жесткой опорой. Такие купола могут быть запроектированы с шарнирными узлами.
Потеря устойчивости шарнирно-стержневых сетчатых куполов заключается в продавливают к центру кривизны одного из наиболее загруженных узлов. Критическая узловая нагрузка
Fcr = 2EAβ3p.
(6.62)
301
При изменении ξ в интервале 0 ≤ ξ ≤ 1 параметр р есть максимальное значение функции
p0 =
| ξ (1 - ξ0 - ξ) (2 - 2ξ0 - ξ) |
| 1(1 - m) + 2(2m + 1) (ξ0 + ξ) |
,
(6.63)
где ξ = α / β - безразмерный параметр прогиба узла; ξ0 = α0 / β - безразмерный параметр начального прогиба узла; m = F2 / F1 - параметр неравномерности нагружения соседних узлов; α - угол поворота стержня в радиальной плоскости в процессе деформирования; α0 - начальный угол поворота стержня по отношению к номинальному положению; F1 - нагрузка на рассматриваемый узел; F2 - нагрузка на соседний узел.
Начальные неправильности формы, заключающиеся в отклонении отдельных узлов от исходной сферической поверхности, возникают в результате неточности изготовления отдельных стержней. Расчетное значение параметра ξ0 можно вычислить по формуле
ξ0 = 0,65
.
(6.64)
Напоминаем, что в (6.64) δ - допуск при изготовлении отдельных стержней.
Коэффициенты неравномерности загружения для постоянной и ветровой нагрузок близки к единице. Коэффициент неравномерности для снеговой нагрузки может быть принят равным 0,5.
Максимальная узловая нагрузка должна быть меньше критической, вычисленной по формуле (6.62),
F < Fcr.
(6.65)
Однако это условие является необходимым, но не достаточным. Любые угловые перемещения стержней (α > 0) приводят к увеличению усилий в них, что необходимо учитывать при проверке несущей способности. Коэффициент возрастания продольной силы может быть вычислен
k1 = 1 / (1 - δ0 - δ).
(6.66)
Значение δ определяют из решения уравнения (6.63) при
p = F1 / Fкр,
где F - расчетная узловая нагрузка. Проверка устойчивости каждого стержня должна выполняться на расчетные усилия, полученные в упругой стадии, умноженные на коэффициент k1. Как уже отмечалось выше, не следует допускать значений коэффициента нелинейного возрастания усилий более 1,1...1,15. Рекомендуется также принимать гибкость
302
стержней не более λ = 80...90, в противном случае необходимо дополнительно учитывать влияние снижения их продольной жесткости на величину критической нагрузки.
Пример. Требуется подобрать сечения стержней сферического сетчатого купола диаметром 6 м с высотой подъема f = 0,75 м (рис. 6.24). Разрезка поверхностей типа "Ромб". Средняя длина стержня l = 780 мм; узлы сопряжения - шарнирные; нагрузка равномерно распределенная интенсивностью q = 2,4 кН/м2.
Определим радиус кривизны купола (рис. 6.24, б)
R =
=
= 6,375 м.
Максимальные усилия в стержнях купола могут быть определены по формуле (6.57)
N = kgRl,
где k = 0,36 - коэффициент, зависящий от угловой координаты φ стержня, определяемый по табл. 6.4,
N = 0,36 · 2,4 · 6,375 · 0,78 = 4,295 кН.
Сечение стержня будем подбирать по устойчивости как центрально-сжатого элемента [1], а затем проверять устойчивость узла сетчатого купола под нагрузкой (предотвращение прощелкивания узла).
Для расчета последнего предварительно определим следующие параметры:
- b = l / 2R = 0,78 / 2 · 6,375 = 0,0612 - угол наклона стержня к касательной плоскости в узле;
- δ0 = 0,65
= 0,65
= 0,342 - безразмерный параметр. Начальные перемещения узла, определяемые по формуле (6.64), происходят из-за наличия отступления в изготовлении отдельных стержней δ = 1,5 м.
 Рис. 6.24. Сетчатый сферический купол
Рис. 6.24. Сетчатый сферический купол
303
 Рис. 6.25. Грузовая площадь узла
Рис. 6.25. Грузовая площадь узла
Усилие в стержне с учетом его возрастания в процессе деформирования стержневой системы определяется расчетом по деформированной схеме
Nef = Nk1,
где k1 - коэффициент возрастания продольной силы, определяемый по формуле (6.66),
k1 =
=
= 2,183,
где δ = 0,2 определено из решения уравнения (6.63) при р = р0 = 1.
Тогда Nef = 2,183 · 4,295 = 9,376 кН.
Подберем трубчатое сечение стального стержня с расчетным сопротивлением Ry = 210 МПа из условия устойчивости. Для этого зададимся гибкостью λ = 80, которой соответствует φ = 0,734. Коэффициент условий работы для таких конструкций принимают γс = 0,7. Имея эти данные, определим требуемую площадь
A ≥
=
= 0,91 см2.
Принимаем стальную круглую трубу d = 40 мм с толщиной стенки t = 2 мм. В этом случае площадь поперечного сечения А = 2,386 см2.
Теперь проведем расчет на устойчивость узла. Для этого предварительно определим грузовую площадь узла Su (рис. 6.25).
При этом считаем, что все стороны одинаковой длины и, следовательно, треугольники сетчатой поверхности равносторонние. Грузовая площадь Su равна площади двух треугольников, образованных стержнями решетки,
Su = 2 · 0,433l2 = 2 ̭ 0,433 · 0,782 = 0,528 м2.
Тогда узловая нагрузка
F = Suq = 0,528 · 2,4 = 1,26 кН.
Критическую нагрузку на узел определяем по формуле (6.62)
Fcr = 2EA · β3 · p = 2 · 2,1 · 104 · 2,386 · 0,06123 · 0,088 = 2,02 кН,
где р = 0,088 находим по графику (рис. 6.22).
Устойчивость узла обеспечена, поскольку F = 1,26 кН < Fcr = 2,02 кН.
- 1...7. См. основную литературу.
- 8. Липницкий М.Е. Купола: расчет и проектирование. - Л.: Стройиздат, 1973.
- 9. Современные пространственные конструкции / Под ред. Ю.А. Дыховичного, Э.З. Жуковского. - М.: Высшая школа, 1991.
- 10. Трофимов В.И., Каминский А.М. Легкие металлические конструкции зданий и сооружений. - М.: Наука, 1997.
- 11. Липницкий М.Е. Купольные покрытия для строительства в условиях сурового климата. - Л.: Стройиздат, 1981.
304
