Ребристый купол при расчете на вертикальную, симметричную относительно оси купола нагрузку может быть расчленен на отдельные плоские арки, каждая из которых воспринимает нагрузку с приходящейся на
284
нее грузовой площади. Если распор купола воспринимается опорным кольцом, то кольцо может быть заменено условной затяжкой, находящейся в плоскости каждой пары ребер, образующих плоскую арку [11].
Площадь сечения условной затяжки принимают такой, чтобы ее упругие деформации были равны упругим деформациям кольца в диаметральном направлении от горизонтальных реакций всех ребер (рис. 6.16).
При частом расположении ребер купола действие их распоров на кольцо можно привести к равномерно распределенной нагрузке (рис. 6.16, б):
р = (пН) / (2πr),
(6.1)
где п - количество ребер в куполе; H - распор одного ребра (арки); r - радиус опорного кольца купола.
Тогда растягивающее усилие в кольце от единичных распоров
Nk = pr = n / 2π.
(6.2)
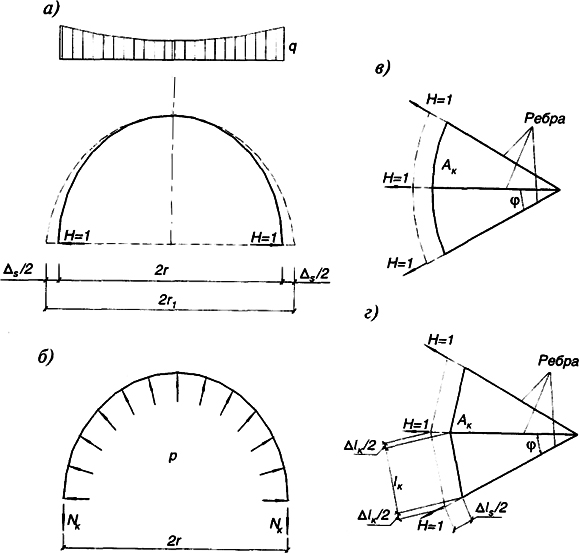 Рис. 6.16. К расчету ребристого купола на вертикальную нагрузку:a
Рис. 6.16. К расчету ребристого купола на вертикальную нагрузку:a - схема условной арки;
б, в - расчетные схемы кольца;
г - деформация многоугольного кольца
285
Увеличение длины кольца в результате растяжения
Δlk = (Nk2πr) / (EkAk) = (nr) / (EkAk).
(6.3)
Увеличение диаметра кольца Δk получаем из равенства 2πr + Δlk = 2πr1, откуда
Δk = 2r1 - 2r = (Δlk) / π = (nr) / (πEkAk).
(6.4)
Удлинение условной плоской затяжки от единичного распора арки H = 1 (рис. 6.16, а)
Δs =
=
,
(6.5)
где EsAs - жесткость сечения условной затяжки.
Приравнивая удлинения условной затяжки к увеличению диаметра кольца 2r / (EsAs) = (nr) / (πEkAk), определяем площадь сечения условной затяжки
As = (2πEkAk) / (nEs).
(6.6)
Если кольцо имеет вид многоугольника, то аналогичными выкладками можно получить площадь сечения условной затяжки, эквивалентной кольцу по упругим деформациям (рис. 6.16, г)
As =
sin2
,
(6.7)
где lk - длина прямолинейного участка многоугольника; φ - угол между горизонтальными проекциями смежных ребер.
После такой замены опорного кольца условной затяжкой можно производить обычный расчет плоской арки с затяжкой, имеющей площадь поперечного сечения, равной As.
Верхнее кольцо, работающее на сжатие, должно быть проверено на прочность, если оно имеет ослабление сечения,
σ = Nk / Аkv = ρvrv / Аkv ≤ Ryγc,
(6.8)
и на устойчивость
Nkv = ρvrv ≤ Ncr = (3EIkv) / rv2,
(6.9)
где rv, Akv - соответственно радиус и площадь сечения верхнего кольца; ρv = (nH) / (2πrv) - действия распоров, приведенные к равномерному давлению; Ikv - момент инерции сечения верхнего кольца относительно вертикальной оси.
286
При расчете купола на горизонтальную ветровую или несимметричную вертикальную нагрузку конструкцию купола расчленяют на диаметрально расположенные арки. Арка, получающая от нагрузки наибольшее горизонтальное смещение, испытывает упругий отпор других арок, расположенных под углом к ней. Если для простоты расчета предположить, что горизонтальные сечения купола смещаются в горизонтальном направлении одно относительно другого без поперечных деформаций, то упругий отпор можно считать приложенным в ключе арки.
Схема воздействия нормальной составляющей ветровой нагрузки на купол изображена на рис. 6.17, а.
Аэродинамические коэффициенты даны в табл. 6.1. Купол разбивают на четыре квадранта: в первом и третьем квадрантах равнодействующие ветрового давления действуют в одном направлении и вызывают горизонтальное смещение; во втором и четвертом квадрантах ветер действует в противоположных направлениях и горизонтальных смещений купола не вызывает.
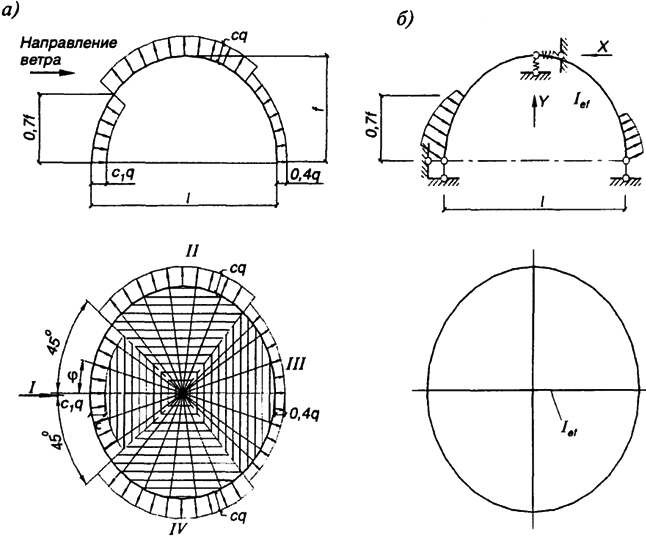 Рис. 6.17. К расчету ребристого купола на ветровую нагрузку:a
Рис. 6.17. К расчету ребристого купола на ветровую нагрузку:a - схема ветровой нагрузки;
б - расчетная схема
287
Таблица 6.1. Значения аэродинамических коэффициентов с и с1
| f / l |
0,5 |
0,4 |
0,3 |
0,2 |
| с |
1,2 |
1,1 |
1 |
0,9 |
| с1 |
0,7 |
0,6 |
0,4 |
0,3 |
Наибольшее смещение получает расчетная арка, расположенная в плоскости равнодействующей ветрового давления в первом и третьем квадрантах.
Все арки, расположенные в первом и третьем квадрантах, можно рассматривать как одну эквивалентную арку с моментом инерции
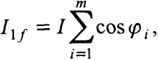 (6.10)
(6.10)
где I - момент инерции сечения одной арки; φi - угол наклона i-й арки к направлению равнодействующей ветровой нагрузки; т - число арок первого и третьего квадрантов (рис. 6.17).
Эквивалентную арку рассчитывают на ветровое давление, приложенное только к части арки (2/3 ее длины), примыкающей к опорам (рис. 6.17). Средняя часть арки по длине испытывает симметричный отсос, не влияющий на горизонтальное смещение. Арки, расположенные во втором и четвертом квадрантах, оказывают упругое противодействие перемещениям в ключе рассматриваемой эквивалентной арки. Горизонтальная и вертикальная податливость ключевого сопряжения соответственно равны:
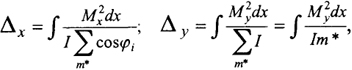 (6.11)
(6.11)
где Мх, My - изгибающие моменты в арках от сил Х = 1 и У = 1 (рис. 6.17); суммы ∑ относятся к аркам второго и четвертого квадрантов; т* - число арок в указанных квадрантах.
Считая эквивалентную арку для простоты трехшарнирной, получим по методу сил систему уравнений для определения неизвестных реакций X и У:
δххX + δхуY + δрх = ΔxX;
δхyX + δyуY + δрy = ΔyX;
(6.12)
где δху = δух = 0; δрх и δру - перемещения арки от ветровой нагрузки;
288
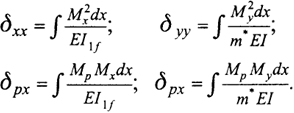 (6.13)
(6.13)
Найдя Х и У из уравнений (6.12), легко можно определить опорные реакции в трехшарнирной статически определимой арке. Усилия, полученные для эквивалентной арки, распределяются по аркам первого и третьего квадрантов пропорционально их приведенным жесткостям. В наиболее нагруженной арке, расположенной по направлению действия ветра, усилие может быть получено делением усилия в эквивалентной арке на величину 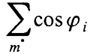 .
.
289
