Формообразование ребристых, ребристо-кольцевых и ребристо-кольцевых со связями куполов сводится к определению формы и координат плоской арки, образованной из двух диаметральных ребер [11]. Форму арки определяют на этапе архитектурного проектирования, расчет координат ведут по известным формулам аналитической геометрии.
Формообразование сетчатых и пластинчатых куполов является более сложным процессом. Поэтому остановимся на этом вопросе подробнее.
Выбор и расчет геометрической схемы купола является первой и очень ответственной стадией проектирования, так как именно от этого зависит число типоразмеров элементов, конструкция узлов сопряжений, способы изготовления и монтажа элементов и в конечном итоге эффективность конструкции.
В процессе формообразования поверхности купола можно выделить три этапа: 1) выбор поверхности; 2) выбор способа разрезки (под термином "разрезка" понимается способ нанесения на выбранную поверхность сети геометрических линий каркаса купола); 3) расчет координат узлов.
Поверхности сетчатых оболочек, в основном, ограничиваются двумя классами: поверхности параллельного переноса (эллиптический параболоид,
275
круговая поверхность переноса, гиперболический параболоид) и поверхности вращения (сфера и др.).
Преобладающее количество сетчатых куполов построено на сфере, поэтому дальнейшее рассмотрение вопросов формообразования сетчатых куполов будем проводить, исходя из построений на сфере.
Для оболочек вращения очень часто за основу принимают меридионально-кольцевую систему разрезки. Суть этой системы заключается в членении поверхности вращения меридиональными и параллельными плоскостями на треугольные (у полюса) и трапециевидные элементы (рис. 6.8).
Число типоразмеров треугольных и трапециевидных элементов при этой системе разрезки определяется числом ярусов между параллельными сечениями и не зависит от числа меридиональных сечений, а также от формы меридиональной образующей кривой. При формообразовании сферических сетчатых оболочек на плане, близком прямоугольному, используют также сеть меридианов, образованную пересечением со сферой двух пучков плоскостей с взаимно-перпендикулярными осями. Как видно из схемы рис. 6.8.5, число типоразмеров элементов при такой разрезке значительно больше, чем при меридионально-кольцевой системе.
Наибольшее распространение из сетчатых оболочек вращения получили сетчатые сферические купола на круглом и многоугольном (вписанном в круг) плане. Системы разрезок таких куполов многообразны. Можно различить два основных этапа построения этих систем. Вначале производят первичную разбивку шарового сегмента на определенное число одинаковых участков, а затем выполняют окончательную разрезку каждого полученного участка на более мелкие. Первичную разбивку в основном осуществляют по меридиональной схеме или по схемам правильных и полуправильных многогранников.
Звездчатая система (рис. 6.9). Первичная разбивка такой системы - меридиональная. На сферический сегмент наносят сеть меридианов. Каждый полученный участок делят четырехугольными ячейками таким образом, чтобы два противоположных узла ячейки располагались на одном меридиане, а два других - на одной параллели.
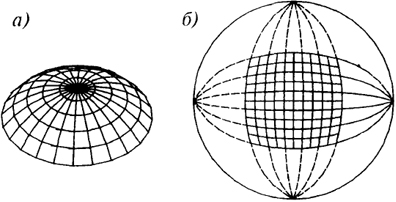Рис. 6.8. Формирование сетки купола по способу разрезки сферы:а - меридионально-кольцевая разрезка;
б - разрезка сферы двумя пучками меридиональных плоскостей с взаимно перпендикулярными осями
276
Может быть построено две разновидности сетей, применяемых для этой системы разрезки, - правильная сеть Чебышева и сеть локсодромий.
Применение правильной сети Чебышева (рис. 6.9, а) приводит к сгущению сетки по мере приближения к полюсу купола. Использование сети локсодролий (линий, имеющих постоянный угол наклона к меридиану) частично устраняет этот недостаток, однако значительное уменьшение длины боковых сторон треугольников также вызывает сгущение сетки (рис. 6.9, б).
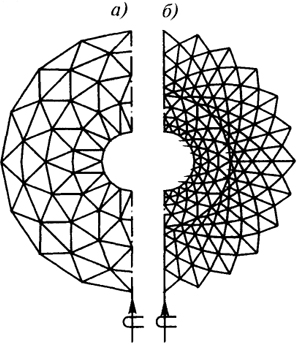Рис. 6.9. Звездчатая система:а - на основе сети Чебышева; б - на основе сети локсодромий
В звездчатой системе с применением сети Чебышева длина стержней вдоль линий сети постоянна, хотя изменение углов между стержнями приводит к тому, что число узловых элементов равно числу ярусов. При локсодромной разрезке, наоборот, узловые элементы могут быть одного типоразмера, а число типоразмеров стержней, расположенных вдоль линий сети, может быть равно числу ярусов.
Система Кайвитта. Эта система устраняет основной недостаток звездчатой системы - сгущение сетки. Первичная разбивка - меридиональная. Основание каждого полученного сектора делят на определенное количество равных участков, а затем проводят кольцевые сечения, число которых равно числу членений основания. Каждое кольцевое сечение делят на равные части, число которых в каждом последующем сечении, считая от основания сектора, уменьшают на единицу (рис. 6.10). Полученные точки соединяют и таким образом получают сеть треугольников, основание которых вдоль каждого яруса, как и в звездчатой системе, равны. Однако образованные таким способом треугольники в отличие от звездчатой
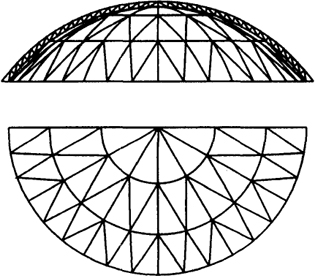Рис. 6.10. Система Кайвитта
277
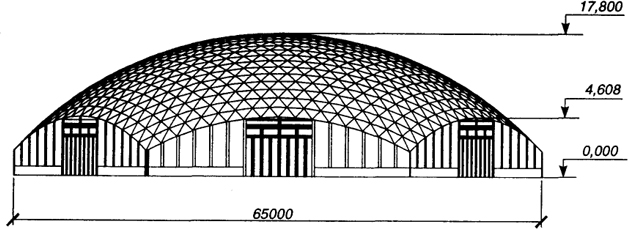Рис. 6.11. Купол диаметром 65 м в Душанбе (разрезка системы "Ромб-1")
схемы неравнобедренные, поэтому число их типоразмеров соответствует квадрату числа членений (ярусов).
Система "Ромб-1". Сущность этой системы заключается в первичном меридиональном делении купола на сектора с последующим членением каждого сектора на ромбовидные ячейки путем нанесения правильной сети Чебышева. Если в звездчатой схеме противоположные узлы ячейки сети расположены на меридианах или соответственно на параллелях, то в данной системе линии сети Чебышева различных направлений располагаются вдоль боковых сторон сектора.
В результате такой разбивки получается достаточно равномерная сеть из равнобедренных треугольников, число типоразмеров которых приблизительно в два раза меньше, чем в системе Кайвитта. Система "Ромб-1" применена, в частности, при проектировании купола диаметром 65 м в Душанбе (рис. 6.11).
В отличие от звездчатой системы и системы Кайвитта основания секторов купола не совпадают с кольцевыми сечениями и образуют пространственную (неплоскую) кривую. Поэтому формообразование круглых в плане покрытий по данной системе затруднено.
Системы, основанные на применении многогранников, вписанных в сферу. Купола на основе этой системы выкраивают из сферы, первичную разбивку которой производят по геодезическим линиям, проведенным через вершины вписанных многогранников.
В качестве таких многогранников обычно используют додекаэдр (12 пятиугольных граней) и икосаэдр (20 треугольных граней).
Для сферических куполов большой высоты рационально использование симметрии правильных многогранников икосаэдра и додекаэдра. Они имеют десять тройных осей вращения и шесть зеркально-поворотных осей десятого порядка. Предложено большое количество вариантов
278
построения сферических сетей с использованием симметрии правильных многогранников. В практике проектирования наибольшее, распространение получили два способа: геодезическая сеть на основе додекаэдра (рис. 6.12, а); построение 720-гранника на основе усеченного икосаэдра (рис. 6.12, б).
Рис. 6.12. Схемы построения сферической сети на основе:а - додекаэдра;
б - икосаэдра
279
