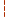|
|
 |
 |
 |
 |
Расчет опорных шарниров для арок небольших пролетов (рис. 5.7, а) производится аналогично расчету баз центрально-сжатых колонн, что касается определения размеров в плане и толщины опорной плиты. Разница состоит в том, что фундаментные болты необходимо проверить на срез под действием поперечной силы и на растяжение под действием растягивающей силы N, которая может возникнуть от действия ветра в легких арках.
Плиточные шарниры (см. рис. 5.7, б) рассчитывают на смятие при свободном касании по формуле
≤ Rcdγc,
(5.25)
где N - нормальная сила на опоре; r, l - радиус кривизны и длина плиты; Rcd - расчетное сопротивление стали при свободном касании.
Необходимая толщина плиты t определяется из условия ее работы на изгиб как консоли при равномерном загружении опорным давлением по верхней поверхности (см. рис. 5.7, б) интенсивностью σ = N / al
t = √
.
(5.26)
Балансирные и пятниковые шарниры передают давление на нижнюю часть шарнира при плотном касании (см. рис. 5.7, в - г). Напряжения сжатия в цапфе распределяются неравномерно от максимального значения по вертикальной оси до нуля на границе балансира (см. рис. 5.7, г).
Можно предположить, что напряжения по цилиндрической поверхности цапфы распределяются по закону косинуса и линию контакта в запас ограничить углом π / 2. Тогда наибольшее напряжение в цапфе можно получить из выражения
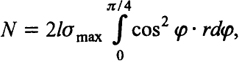(5.27)
откуда
σmax =
≤ Rlp,
(5.28)
где Rlp - расчетное сопротивление на местное смятие в цилиндрических шарнирах при плотном касании; l, d - длина и диаметр цапфы.
Подошва балансира подобно опорным плитам баз рассчитывается на изгиб под равномерным опором фундамента σ = N / al.
268
Рис. 5.14. Схемы нагрузок на арку
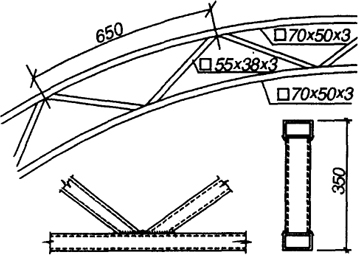Рис. 5.15. Конструкция сквозной арки
В бесшарнирных арках узлы опирания на фундаменты конструируются и рассчитываются аналогично рамным конструкциям. Ниже в примере приведена конструкция опоры для легкой бесшарнирной арки (рис. 5.16).
Пример 5.1. Требуется проверить прочность и устойчивость круговой бесшарнирной арки сквозного и сплошного сечения. Генеральные размеры арки показаны на рис. 5.14. Шаг арок - 3 м. Система связей и прогонов между арками обеспечивает крепление их из плоскости через 1,95 м. Район строительства г. Санкт-Петербург.
Расчетная нагрузка от собственного веса покрытия и арки составляет 0,5 кН/м2. Снеговая нагрузка 1,0 кН/м2 · 1,6 = 1,6 кН/м2. Ветровая нагрузка - 0,3 · 1,4 = 0,42 кН/м2 (1,6 и 1,4 - коэффициенты надежности по нагрузке). Нагрузки на арку составляют: собственный вес - q = 0,5 кН/м2 · 3 м = 1,5 кН/м; снег - р = 1,6 · 3 = 4,8 кН/м; ветер - qv = 0,42 · 3 = 1,26 кН/м. В соответствии с [6] схемы загружения арки от указанных нагрузок показаны на рис. 5.14.
По результатам статического расчета арки от каждой нагрузки были определены наихудшие комбинации усилий, которые составили: Мmах = 27,7 кН/м, N = 35,8 кН, Q = 20,9 кН. Такая комбинация оказалась в опорном сечении. Следует отметить, что действие ветровой нагрузки оказывало разгружающее влияние и поэтому при определении указанных комбинаций не учитывалась.
Элементы сквозной арки (рис. 5.15) выполнены из гнутосварных замкнутых профилей сечением: пояса - 70 × 40 × 3 мм (Af = 6,24 см2, ix = 2,53, iy = 1,62 см); решетка - 60 × 25 × 2,5 мм (Ad = 4,00 см2, ix = 2,07 см, iy = 1,02 см). Полная высота сечения сквозной арки 350 мм. Материал - сталь марки ВСт. 3 пс 6-1 с расчетным сопротивлением Ry = 240 МПа.
Расчетные длины поясов в плоскости арки lef,y = 65 см, из плоскости арки lef,x = 195 см. Расчетные длины раскосов lef,x = lef,y = 0,9 · 44,2 = 39,8 см. Усилия: в поясах - Nf =
+
=
+
= 107,2 кН; в раскосах - Nd =
=
= 30,8 кН.
Узел опирания показан на рис. 5.16.
269
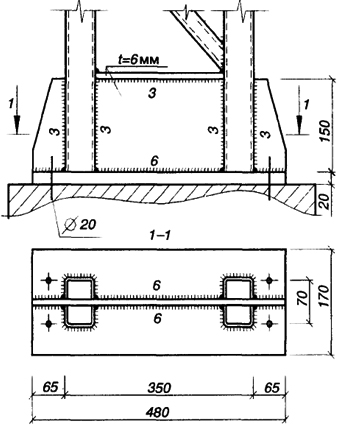Рис. 5.16. Конструкция опоры бесшарнирной сквозной арки
Расчет на устойчивость поясов
λx =
=
= 77; λy =
=
= 40; φmin = 0,706;
=
= 238,4 МПа ≤ Ryγc = 240 МПа.
Расчет на устойчивость раскосов
λx =
=
= 19; λy =
=
= 39; φmin = 0,89;
=
= 84,7 МПа ≤ Ryγc = 240 МПа.
Устойчивость элементов поясов и решетки обеспечена.
Расчет арки на устойчивость в ее плоскости на действие осевых сил проводят по формуле
Ncr = π2EJx |
| μ2S2,
где Jx = kJx0 = 0,8(2 · 6,24 · 15,52 + 2 · 16,37) = 2425 см4; k = 0,8 - коэффициент, учитывающий податливость решетки; S - длина дуги полуарки; μ = 0,85 - коэффициент расчетной длины;
Ncr =
| 3,142 · 2,06 · 105 · 2425 |
| 0,852 · 11782 · 9,8 |
= 501,8 кН >> 1,4N = 1,4 · 39,2 = 54,9 кН,
где N = 39,2 кН - продольная сила в четверти длины арки. Устойчивость арки в ее плоскости обеспечена.
270
Арка сплошного сечения выполнена из двутавра N18Б2. Геометрические характеристики сечения А = 23,95 см2, Jx = 1317см4, Wx = 146,3 см3, ix = 7,41 см, iy = 2,05 cм, ρx = 6,1 см.
Расчет арки на устойчивость в ее плоскости на действие осевых сил
Ncr =
| 3,142 · 2,06 · 105 · 1317 |
| 0,852 · 11782 · 9,8 |
= 272,5 кН >> 1,4N = 1,4 · 39,2 = 54,9 кН,
Устойчивость арки в ее плоскости обеспечена.
Расчет арки на устойчивость из ее плоскости (по изгибно-крутильной форме) выполняем в следующей последовательности.
Усилия в четверти длины арки N = 39,2 кН, М = 15,97 кН·м
Расчетная длина из плоскости арки lef,y = 195 см
λy =
=
= 96, φy = 0,57, e =
= 40,75.
При mx =
=
= 6,68 и λ c = π √
= 92 < λ y = 96, с = 0,133;
=
| 39,2 · 9,8 |
| 0,133 · 0,57 · 23,95 |
= 211,5 МПа ≤ Ryγc = 240 МПа.
Устойчивость арки из ее плоскости обеспечена.
Расчет арки на прочность
σ =
+
=
+
= 200 МПа < Ryγc = 240 МПа.
Прочность арки обеспечена.
* Пример расчета подготовлен канд. техн. наук, доц. Н.Н. Родиковым.
271
|
 |
 |
 |
 |
|
