При расчете арочное покрытие расчленяют на отдельные плоские арки. Расчет производится обычными методами строительной механики. Статически неопределимые арки удобно рассчитывать методом сил. Двухшарнирная арка один раз статически неопределима, за лишнее неизвестное принимают распор. Решают каноническое уравнение и определяют неизвестный распор для каждого вида загружения. В большепролетных арках для получения более точных результатов при вычислении перемещений следует учитывать обжатие арки от нормальных сил. При наличии затяжки ее упругие перемещения учитывают всегда.
После определения неизвестного распора усилия M, N, Q в любом сечении на расстоянии х от левой опоры (см. рис. 5.12) находят по формулам
262
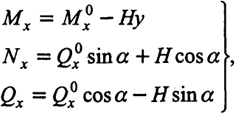 (5.4)
(5.4)
где
H - распор;
Mx0,
Qx0 - как в простой балке пролета
l; α - угол наклона оси арки в сечении х к горизонту.
По приведенным формулам для постоянной и временных нагрузок строят соответствующие эпюры (для сплошных арок эпюру Q обычно не строят). Эпюры строят по нескольким сечениям на полупролете арки. Выбор количества сечений на полупролете зависит от очертания арки и величины пролета и колеблется от 5 до 12 и более, включая сечения на опоре и в ключе. Затем находят невыгодные комбинации M и N, которые могут быть не обязательно в четверти пролета.
Бесшарнирные арки трижды статически неопределимы. При их расчете удобно выбирать основную систему, разрезая арку в ключе и прикладывая неизвестные. Для уменьшения вычислительной работы можно использовать метод жестких консолей. После раскрытия статической неопределимости усилия в арке определяют по формулам (5.4) с построением эпюр и нахождением невыгодных сочетаний М и N. В арках, особенно пологих, с развитым по высоте сечением следует учитывать температурные напряжения, которые могут быть определены по формулам, МПа:
в двухшарнирной арке
σ = ±2,36 · Δt · h / f;
(5.5)
в бесшарнирной арке
| в пролете |
σ1 = ±4,72 · Δt · h / f; |
(5.6) |
| на опоре |
σ2 = ±9,44 · Δt · h / f, |
(5.7) |
где Δf - изменение температуры, °С; h / f - отношение высоты сечения арки к стреле подъема.
После определения невыгодных комбинаций М и N проверку прочности сплошных арок производят как для внецентренно сжатых элементов при упругой работе стали
σ =
+
≤ Ryγc.
(5.8)
Усилия в элементах сквозных арок с параллельными поясами (рис. 5.12) определяют через Мх, Nx, Qx по формулам:
263
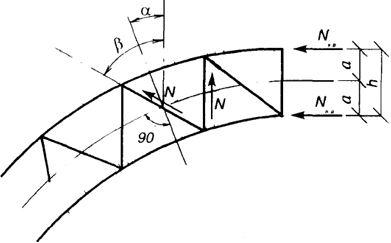 Рис. 5.12. К расчету сечений элементов сквозной арки
Рис. 5.12. К расчету сечений элементов сквозной арки
в верхнем поясе
Nvp = -Nx
-
;
(5.9)
в нижнем поясе
Nnp = -Nx
-
;
(5.10)
в раскосе
Nd =
;
(5.11)
в вертикальных стойках
Ns =
;
(5.12)
при расположении стойки перпендикулярно поясам
Ns = Qx.
(5.13)
Кроме проверки прочности сплошной арки по формуле (5.8) необходимо проверить устойчивость арки из ее плоскости на участке между точками, закрепленными в горизонтальном направлении системой связей и прогонами. В арках большого пролета влияние нормальной силы существенно больше, чем моментов, поэтому такую проверку можно производить как для центрально сжатого стержня по формуле
≤ Ryγc,
(5.14)
где <ру определяется по гибкости относительно вертикальной оси сечения арки. В арках малых и средних пролетов влияние моментов от временных нагрузок может быть более существенным. Поэтому проверку устойчивости из плоскости следует производить с учетом влияния моментов по формуле
≤ Ryγc,
(5.15)
264
 Рис. 5.13. К расчету арок торцевого блока:а
Рис. 5.13. К расчету арок торцевого блока:а - для пологих арок;
б - для высоких арок
В решетчатых арках, в элементах которых усилия определяются по формулам (5.9)...(5.13), проверка устойчивости производится как для центрально-сжатых элементов аналогично фермам.
При расчете сквозных арок больших пролетов следует выполнить уточняющий расчет и определить величину распора для каждой нагрузки с учетом предварительно подобранных сечений.
Для двухшарнирной арки распор определяется из канонического уравнения
δ11H + Δ1p = 0,
(5.16)
где перемещения вычисляются по формулам:
Таблица 5.1. Значения k1 для круговой симметричной арки
| f / l |
Значения k1 для арки |
| бесшарнирной |
двухшарнирной |
трехшарнирной |
| 0,1 |
58,9 |
28,4 |
22,2 |
| 0,2 |
90,4 |
39,3 |
33,5 |
| 0,3 |
93,4 |
40,9 |
34,9 |
| 0,4 |
80,7 |
32,8 |
30,2 |
| 0,5 |
64,0 |
24,0 |
24,0 |
265
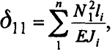 (5.17)
(5.17)
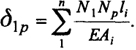 (5.18)
(5.18)
При вычислении перемещений можно ограничиться суммированием только по поясам, пренебрегая перемещениями в стержнях решетки, незначительно влияющими на величину распора.
Арка как криволинейный сжатый брус требует проверки общей устойчивости в своей плоскости. Устойчивость кривой арки можно проверить по выражению
(1,3 ÷ 1,4)p ≤ pcr = k1
(5.19)
где р - нагрузка на единицу длины арки; 1,3...1,4 - коэффициент безопасности на устойчивость; рсr - критическая нагрузка; Jx - момент инерции сечения арки относительно горизонтальной оси; k1 - коэффициент, принимаемый по табл. 5.1.
Устойчивость параболической арки постоянного сечения при равномерно распределенной вертикальной нагрузке можно проверить по формуле (5.18), но с введением коэффициента k (табл. 5.2) вместо k1.
Проверка устойчивости арки может быть произведена приближенно как для центрально-сжатого стержня с расчетной длиной равной μS, которая обусловлена наиболее вероятной формой потери устойчивости арки (см. рис. 5.11, а). Условие устойчивости записывается
(1,3 ÷ 1,4)N ≤ Ncr =
,
(5.20)
где S - длина полуарки; μ - коэффициент расчетной длины, принимаемый по табл. 5.3.
При расчете высоких арок следует учитывать дополнительные усилия, которые возникают в арках торцевого связевого блока при действии ветра на торец здания (рис. 5.13, а). Связевой блок (ферму) рассматривают как пространственную оболочку, состоящую из поясов двух соседних арок, соединенных диагоналями и распорками (рис. 5.13, б). Исключая сжатые диагонали из работы, можно получить усилия в растянутых диагоналях, спроектировав все действующие силы в разрезе I - I на направление раскоса
Nd = Q / cos ψ,
(5.21)
266
Таблица 5.2. Коэффициент k параболической арки
| f / l |
Значения k в ярке |
| бесшарннрной |
двухшарнирной |
трехшарнирной |
| 0,1 |
60,7 |
28,5 |
22,5 |
| 0,2 |
101 |
45,4 |
39,6 |
| 0,3 |
115 |
46,5 |
46,5 |
| 0,4 |
111 |
43,9 |
43,9 |
| 0,5 |
97,4 |
38,4 |
38,4 |
| 0,6 |
83,8 |
30,5 |
30,5 |
Таблица 5.3. Коэффициент μ расчетной длины арки
| Арка |
Значения μ при f / l |
| 0,05 |
0,2 |
0,3 |
0,4 |
| Трехшарнирная |
1,2 |
1,2 |
1,2 |
1,3 |
| Двухшарнирная |
1 |
1,1 |
1,2 |
1,3 |
| Бесшарнирная |
0,7 |
0,75 |
0,8 |
0,85 |
где Q - поперечная сила от ветровой нагрузки в рассматриваемом сечении; ψ - угол между диагональю и распоркой.
Отделив одну арку от другой продольным разрезом II - II, разложим усилие в диагонали на усилие по направлению пояса
Np = Nd sin ψ
(5.22)
и усилие по направлению распорки
Ns = Nd cos ψ.
(5.23)
Отрезанная арка находится в равновесии и ее следует рассчитывать на силы, направленные по поясу,
Np = Q tg ψ
(5.24)
как плоскую систему. От действия этих сил определяется распор H, опорные реакции V и усилия N, M, Q.
На передней (торцевой) арке 1 дополнительные ветровые воздействия направлены вверх по образующей и отрывают ее от фундаментов (рис. 5.13, б). На задней арке (арка 2) торцевого блока те же силовые воздействия направлены вниз и прижимают ее к фундаментам. Полученные усилия от ветровой нагрузки складываются с усилиями от собственного веса и веса снега.
267
