Нагрузки, действующие на многоэтажные здания, вызываются силами природы (ветровые, снеговые, гололедные, сейсмические) или деятельностью человека. Величины нагрузок принимают на основании задания на проектирование с обязательным учетом требований норм [6]. Отсылая вас к этим нормам при нештатных ситуациях, приведем данные для наиболее характерных условий.
Постоянные нагрузки от веса несущих и ограждающих конструкций здания по своей природе являются гравитационными. Нормативные значения постоянных нагрузок определяют по данным о весе готовых элементов и изделий или вычисляют по проектным размерам конструкций и плотности материалов.
Нагрузка от веса несущих стальных конструкций может быть предварительно определена по приближенным формулам. Так, нормативная
229
нагрузка от веса несущих конструкций, выполненных из стали С245 (ВСтЗ), может быть подсчитана по формуле, кН/м2 [3]:
р =~ 0,1 + 0,03[q + kw0H / L][1 + 0,01H],
(4.2)
где H и L - соответственно высота и меньший из габаритных размеров здания в плане, м; q - нормативное значение суммы постоянной (кроме веса несущих конструкций) и вертикальной временной нагрузок, отнесенное к площади всех перекрытий (q = 6...10 кН/м2); w0 нормативное ветровое давление для района строительства, кН/м2 (см. табл. П4.2); k - коэффициент, учитывающий конструктивную схему каркаса. Этот коэффициент принимают равным: k = 3 - для обычных рамных систем (см. рис. 4.6, а); k = 1,5 - для секционно-рамных систем и систем с внешней пространственной рамой (см. рис. 4.6, б, в и рис. 4.8, г); k = 2,0 - для связевых систем с решетчатыми стальными диафрагмами или внутренним стволом в виде стальной пространственной фермы (см. рис. 4.8, а, б); k = 1 - для связевых систем с внешними стволами (см. рис. 4.8, в).
Если некоторые несущие конструкции каркаса здания выполнены из стали другой марки с расчетным сопротивлением Ry*, то нормативное значение постоянной нагрузки, кН/м2, может быть вычислено по следующей зависимости [3]:
p* = αр + (1 - α) p(0,3 + 0,7Ry / Ry*),
(4.3)
где α - доля конструкций из стали марки С245; Ry - расчетное сопротивление стали С245.
При расчете ригелей и балок перекрытий учитывают часть нагрузки р, равной (0,3 + 6 / mэт) р - для рамных систем и (0,2 + 4 / mэт) р - для связевых систем, где mэт - число этажей здания (mэт ≥ 20).
Нагрузка от веса стен и перекрытии. Нормативное значение веса 1 м2 стены или перекрытия приближенно составляет, кН/м2:
- для наружных стен из бетонных панелей - 2,5...5,0;
- для стен из эффективных панелей - 0,6...1,2;
- для внутренних стен и перегородок на 30...50 % меньше, чем для наружных стен;
- для несущей плиты перекрытия вместе с полом при использовании железобетонных панелей и настилов - 3...5;
- то же, при использовании монолитных плит из легкого бетона по стальному профнастилу - 1,5...2,0;
- нагрузка от подвесного потолка - 0,3...0,8.
230
Нагрузку от переставляемых перегородок прикладывают в наиболее неблагоприятном для прочности перекрытия сечении.
Временные нагрузки на перекрытия принимают в виде эквивалентных нагрузок, равномерно распределенных по площади перекрытий. Нормативные значения временных нагрузок зависят от назначения зданий и помещений (табл. 4.1).
Таблица 4.1. Нормативные значения равномерно распределенных временных нагрузок на плиты перекрытий
| Здания и помещения |
Нормативные значения нагрузок, кН/м2 |
| 1. Квартиры жилых зданий; жилые помещения домов отдыха, пансионатов, гостиниц; палаты больниц и санаториев; террасы |
1,5 |
| 2. Служебные помещения административного, инженерно-технического, научного персонала организаций и учреждений; классные помещения учреждений просвещения; бытовые помещения общественных зданий |
2,0 |
| 3. Кабинеты и лаборатории учреждений здравоохранения, просвещения, науки; помещения электронно-вычислительных машин; технические этажи |
Не менее 2,0 |
4. Залы: торговые, выставочные и экспозиционные;
собраний и совещаний, концертные и спортивные;
обеденные (в ресторанах, кафе);
читальные |
Не менее 4,0
4,0
3,0
2,0 |
| 5. Книгохранилища; архивы |
Не менее 5,0 |
| 6. Сцены зрелищных предприятий |
Не менее 5,0 |
7. Вестибюли, фойе, коридоры, лестницы, примыкающие к помещениям, указанным в позициях:
а) 1, 2, 3
б) 4, 5, 6 |
3,0
4,0 |
Коэффициенты надежности по нагрузке γ f для равномерно распределенных нагрузок следует принимать равными: γ f = 1,2 - при нормативном значении < 2,0 кН/м2; γ f = 1,3 - при нормативном значении 2,0 кН/м2 и более.
Вероятность одновременного загружения больших площадей перекрытий полной временной нагрузкой не равна единице, поэтому вводят коэффициенты сочетания ψ < 1 на временные нагрузки: ψА1, ψА2 - при расчетах балок и ригелей; ψn1, ψn2 - при определении продольных усилий для расчета колонн, стен и фундаментов, воспринимающих нагрузки от двух и более перекрытий.
231
Для помещений с площадью A > A1 = 9 м2
ψA1 = 0,4 + [0,6 / (A / A1)0,5].
(4.4)
Для помещений при А > А2 = 36 м2
ψA2 = 0,5 + [0,5 / (A / A2)2].
(4.5)
Коэффициенты ψn1 и ψn2 определяют по следующим формулам: для помещений, указанных в поз. 1, 2 и 7а табл. 4.1,
ψn1 = 0,4 + [(ψA1 - 0,4) / n0,5],
(4.6)
для помещений, указанных в поз. 4 и 7б табл. 4.1,
ψn2 = 0,5 + [(ψA2 - 0,5) / n0,5],
(4.7)
где п - общее число перекрытий, нагрузки от которых учитывают при расчете рассматриваемого сечения колонны.
Коэффициенты ψn1 и ψn2 относят к сумме временных нагрузок на нескольких перекрытиях и учитывают при определении только продольных сил. Узловые изгибающие моменты в колоннах следует определять без учета этих коэффициентов, так как основное влияние на величину изгибающих моментов оказывает временная нагрузка на ригелях одного, примыкающего к узлу перекрытия.
При назначении схемы расположения нагрузок необходимо исходить из принципа наиболее неблагоприятного загружения. Так, при определении наибольших пролетных моментов в ригелях рамной системы используют шахматное расположение временных нагрузок, а при расчете рам, стволов жесткости и фундаментов рассматривают не только сплошное загружение всех перекрытий, но и варианты односторонних загружений.
Снеговая нагрузка оказывает влияние только на несущие конструкции покрытия здания и почти не влияет на суммарные усилия в нижерасположенных конструкциях. Закономерности отложения снега на кровлях многоэтажных зданий, в силу их специфики, не исследованы. Поэтому нормативные значения снеговой нагрузки можно определять по правилам проектирования одноэтажных зданий (п. 2.2.1) достаточно смело, поскольку такие нагрузки оказываются выше фактических, так как снег с кровли сдувается ветром, подтаивает и испаряется благодаря некоторым теплопотерям через конструкции покрытия.
Ветровая нагрузка для многоэтажных зданий является наиболее существенной из временных нагрузок. Это вызвано тем, что использование
232
в высотном строительстве стальных и облегченных железобетонных конструкций привело к снижению веса сооружения и сняло ограничения на высоту зданий. С другой стороны, снижение постоянных нагрузок и создание больших, более гибких пространственных решений, привело к значительному снижению жесткости здания. В этих условиях ветровые нагрузки приобрели особое значение.
Действие ветра на сооружения проявляется в виде нагрузки, величина которой зависит от скорости ветра и его порывистости. За нормативную скорость ветра в каждом из 7 ветровых районов принята наибольшая скорость на высоте 10 м над поверхностью земли, превышаемая в среднем раз в 5 лет.
Местные условия рельефа площадки строительства, отличающиеся от условий расположения ближайших метеорологических станций, вносят свои коррективы в величину и характер нормированной для рассматриваемого района скорости ветра.
Записи скорости ветра регистрируются на определенной высоте и характеризуют два явления: достаточно постоянную среднюю скорость ветра и изменяющуюся скорость порывов ветра (рис. 4.15). Следовательно, ветровая нагрузка содержит две составляющие - статическую и динамическую. Динамическую составляющую ветровой нагрузки необходимо учитывать при расчетах многоэтажных зданий высотой более 40 м.
Средняя скорость ветра, т.е. статическая составляющая, возрастает с высотой (см. рис. 4.19, а). Степень ее увеличения зависит от особенностей земной поверхности, так как вблизи земли из-за трения ветер затухает. Чем значительнее влияние окружающих объектов (деревьев, складок ландшафта, зданий), тем на большей высоте скорость ветра достигает максимальной величины. Расчетное значение статической составляющей ветровой нагрузки на высоте z определяется по формуле (2.21) с учетом данных табл. П4.4, табл. 4.2, табл. 4.3 и типа местности (см. 93 [1]). Сооружение считается расположенным в местности данного типа, если эта местность сохраняется с наветренной стороны сооружения на расстоянии 30 Н - при высоте сооружения H до 60 м и 2 км - при большей высоте.
Воздействие ветра более чем на одну вертикальную поверхность здания может вызвать деформации сооружения в двух направлениях (рис. 4.16).
 Рис. 4.15. График изменения скорости ветра:1
Рис. 4.15. График изменения скорости ветра:1 - средняя скорость ветра;
2 - действительная скорость ветра
233
Таблица 4.2. Значения коэффициентов kz для различных типов местности
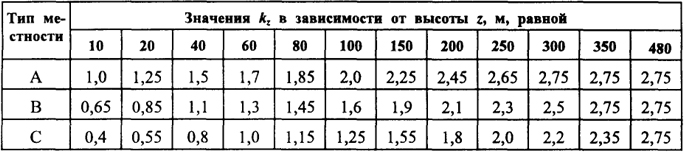
Таблица 4.3. Значения коэффициента общего сопротивления сх при β = 0

Давление ветра всегда является максимальным, если ветер направлен перпендикулярно поверхности здания. Когда воздушный поток подходит к поверхности здания под углом, отличающимся от угла в 90 град., то значительная часть ветрового потока затухает. Однако в этом случае в Несущих конструкциях здания возникают дополнительные напряжения сдвига и кручения, которые не наблюдаются при перемещениях в одном направлении. Поэтому при расчете высотных зданий на ветровую нагрузку рассматривается несколько вариантов загружения (рис. 4.17) при различных значениях аэродинамических коэффициентов с.
 Рис. 4.16. Горизонтальное перемещение каркаса при воздействии ветра на сооружение:а
Рис. 4.16. Горизонтальное перемещение каркаса при воздействии ветра на сооружение:а - схема перемещений;
б - одноосное перемещение;
в - перемещения в двух направлениях; Δ - горизонтальное перемещение каркаса;
1 - статическая составляющая ветровой нагрузки
234
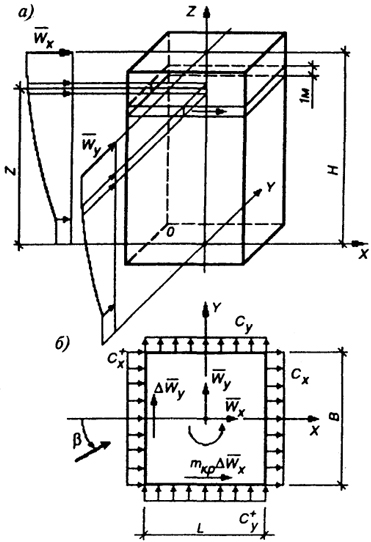 Рис. 4.17. Схема действия ветровой нагрузки на здание:а
Рис. 4.17. Схема действия ветровой нагрузки на здание:а - по высоте;
б - в плане
Средняя составляющая ветровой нагрузки в направлении осей х и у (рис. 4.17, а) на 1 м высоты определяется, как равнодействующая аэродинамических сил, действующих в этих направлениях, и выражается через коэффициент общего сопротивления сх и cу и размеры здания в плане В и L
 (4.8)
(4.8)
где w (z) = wo kzf - расчетное ветровое давление на уровне z.
Для зданий призматической формы с прямоугольным планом B×L при угле атаки ветра β = 0 коэффициент су = 0, а значения коэффициента сх определяются по табл. 4.3, составленной с учетом данных зарубежных и отечественных исследований и норм [3]. Если направление ветрового давления β = 90°, то сх = 0, а значение су находят по той же таблице, поменяв местами на плане здания обозначения В и L.
Для β = 45° значения коэффициентов сх и су приведены в табл. 4.4, при этом более длинной считается сторона плана В, перпендикулярная оси х. Вследствие неравномерного распределения давления ветра на стены при β = 45° и В / L ≥ 2 следует учитывать возможный аэродинамический эксцентриситет в приложении нагрузки wx, перпендикулярной более длинной стороне и равный 0,15 В. Соответствующий крутящий момент, кН/м, на 1 м высоты определяют по формуле:
mкр = 0,15 wcx B2 ,
(4.9)
где сх принимают по табл. 4.3.
Если геометрический центр плана здания не совпадает с центром жесткости несущей системы, то в расчетах необходимо дополнительно учитывать
235
Таблица 4.4. Значения коэффициентов общего сопротивления сх и су при β = 45°
| B/L |
Значения сх и су при H/L, равном |
| 0,25 |
0,5 |
1 |
2 |
5 |
10 |
| 1,0 |
0,9/0,9 |
0,9/0,9 |
1,0/1,0 |
1,0/1,0 |
1,1/1,1 |
1,1/1,1 |
| 4,0 |
1,0/1,0 |
1,1/1,1 |
1,2/1,0 |
1,2/1,0 |
1,2/1,0 |
1,2/1,0 |
крутящие моменты из-за внецентренного приложения ветровой нагрузки (рис. 4.17, б).
Пульсационная составляющая ветрового потока вызывает колебания многоэтажного здания (рис. 4.18, а). Величина пульсационной составляющей ветровой нагрузки в плоскости потока зависит от изменчивости пульсаций скорости vn, характеризуемой стандартом sv (рис. 4.18, б). Ветровое давление в момент времени t может быть вычислено по формуле [3]:
w(t) = w0(1 + ξ) ,
(4.10)
где w0 - среднее значение ветрового давления (статическая составляющая); ξ = 2vn / v - коэффициент пульсаций.
Значения коэффициента пульсаций давления ветра на уровне z от поверхности земли приведены в табл. 4.5, из которой следует, что пульсация ветрового потока с увеличением высоты z уменьшается. Наибольшее влияние на динамические усилия и перемещения оказывают пульсации, частота которых f близка или равна частоте собственных колебаний системы fl.
Нормативное значение пульсационной составляющей ветровой нагрузки wp для многоэтажных зданий с постоянной по высоте жесткостью,
 Рис. 4.18. Воздействие динамической составляющей ветровой нагрузки на многоэтажное здание:а
Рис. 4.18. Воздействие динамической составляющей ветровой нагрузки на многоэтажное здание:а - схема динамических колебаний здания;
б - изменение скорости ветра во времени;
1 - средняя скорость;
2 - скорость порывов ветра;
3 - плотность распределения пульсаций скорости
236
Таблица 4.5. Значения коэффициентов пульсации давления ветра

массой и шириной наветренной поверхности на уровне z допускается определять по формуле:
wp = 1,4 (z / H) ξwm ξ v,
(4.11)
где wm = wo kz с - нормативное значение средней составляющей ветровой нагрузки на высоте z; ξ - коэффициент динамичности, зависящий от частоты f1 первой формы собственных колебаний и логарифмического декремента колебаний δ, равного для многоэтажных зданий 0,3; v - коэффициент, учитывающий пространственную корреляцию пульсации ветра по высоте и фронту здания, составляющий для многоэтажных зданий v = 0,40...0,70 или более точно по данным [6].
Коэффициент динамичности можно определить по табл. 4.6 в зависимости от параметра ε, равного:
ε = (γf / wo)0,5 / 940 f1,
(4.12)
где f1 - частота первой формы собственных колебаний сооружения.
Значения f1 можно принять по приближенным зависимостям: для стальных рамных каркасов f1 =~ 10 / m, Гц; для связевых и рамно-связевых каркасов с железобетонными диафрагмами и стволами жесткости f1 =~ 10 / m, Гц, где m - число этажей здания.
237
Таблица 4.6. Значения коэффициента динамичности ξ ветровой нагрузки для многоэтажных зданий
| εi |
0,05 |
0,075 |
0,10 |
0,15 |
0,20 |
0,25 |
0,3 |
0,4 |
0,45 |
0,5 |
| ξi |
1,60 |
1,75 |
1,85 |
2,0 |
2,1 |
2,13 |
2,2 |
2,28 |
2,3 |
2,3 |
 Рис. 4.19. Суммарная ветровая нагрузка на здание:а
Рис. 4.19. Суммарная ветровая нагрузка на здание:а - фактическая эпюра ветрового давления;
б - эпюра статической составляющей нагрузки
Суммарная ветровая нагрузка на многоэтажное здание представлена на рис. 4.19. Статическая составляющая имеет криволинейную эпюру с ординатами, вычисляемыми по формуле (2.21). Для упрощения расчетов удобно криволинейную эпюру скоростного напора заменять трапецеидальной, эквивалентной ей по изгибающему моменту и поперечной силе в основании здания. Для этого в формуле (2.21) коэффициент kz необходимо заменить на коэффициенты kn и kv, соответствующие ординатам трапеции в нижнем и верхнем сечениях. С погрешностью не более 3 % ординату kn можно считать равной нормативному значению на высоте 5 м в зависимости от местности: для местности типа A kn = 0,75; для местности типа В kn = 0,5; для местности типа С kn = 0,4. Ордината kv в зависимости от высоты здания и типа местности принимает следующие значения [3]:

Ордината на уровне z равна kz = kn + (kv - kn) (z / H). Динамическая составляющая имеет треугольную эпюру, ордината на высоте H в которой может быть вычислена по формуле (4.11) при z = H.
238
