3.2.2. Рамы с элементами переменной жесткости из прокатных двутавров

В следствие дальнейшего совершенствования форм рамных конструкций появились рамы из элементов переменной жесткости. Определяющими нагрузками для бескрановых зданий с рамными каркасами являются нагрузки от конструкций покрытия и снегового покрова. Форма эпюры изгибающих моментов в раме с жестким сопряжением ригеля и стоек при шарнирном сопряжении с фундаментами от этих нагрузок представляет собой параболу в ригеле и треугольники в стойках.

Оптимальной с точки зрения распределения материала будет рама, как можно точнее повторяющая очертание эпюры моментов: максимальные значения высот сечений в коньковом и карнизных узлах и минимальные - в точках пересечения эпюрой моментов нейтральной оси в ригеле и в узлах опирания стоек на фундаменты (рис. 3.7, а). Для упрощения конструкции ригель часто делают постоянного сечения (левая схема на рис. 3.7, б). Все элементы рамы можно изготовить из прокатных двутавров путем соответствующей разрезки. Рамы переменной жесткости позволяют получить экономию стали по сравнению с аналогичными постоянного сечения в среднем до 30% (металлоемкость зависит от габаритных размеров рамы, наличия или отсутствия кранового оборудования, нагрузки на покрытие и др.).

Немаловажным достоинством рам, изготовляемых из прокатных двутавров путем передела, является возможность их производства как на заводах металлоконструкций, так и в условиях небольших специализированных мастерских. Узловые соединения обычно принимают фланцевыми на высокопрочных болтах, что способствует снижению трудозатрат при монтаже.

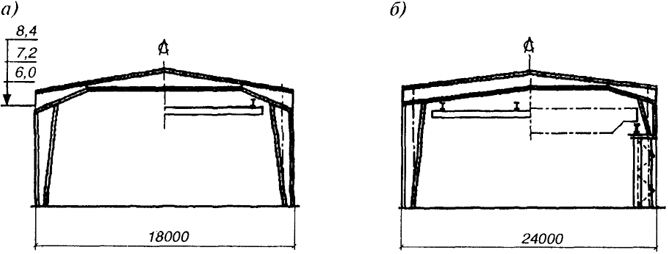Рис. 3.7. Конструктивные схемы рам переменной жесткости

201

Привязанность к сортаменту из прокатных двутавров не позволяет с достаточной свободой назначать размеры сечений элементов. Поэтому следующим этапом развития рам переменной жесткости стали рамы, изготовляемые из листового проката. В таких рамах можно получить экономию стали до 10... 15%, но не более, так как здесь имеются свои трудности, связанные с ограничениями в выборе толщин стенки и полок, ширины полок и высот сечений, определяемые из условий местной устойчивости.

Область применения рам переменной жесткости - от общественных зданий (физкультурно-оздоровительные комплексы, спортивные залы, бассейны и др.) до зданий производственного назначения с возможностью подвески двухопорных кранов грузоподъемностью до 5 т или использования опорных кранов на встроенных эстакадах.

Рамы переменной жесткости дают возможность создавать системы одно- и многопролетных каркасов зданий с широким диапазоном размеров пролетов и высот. Такие системы получили широкое распространение в различных странах, их успешно начинают применять в нашей стране. Системы на основе рам переменной жесткости, производимые фирмой "Батлер" в США и Канаде, завоевали лидирующие позиции в зданиях многоцелевого назначения.

Расчет и конструирование рам переменной жесткости имеют ряд особенностей: взаимосвязь распределения пролетного и карнизного моментов с распределением жесткостей в конструкции; зависимость между максимальным и минимальным сечениями в элементе; специфичность расчета на прочность и устойчивость и др. Так, при расчете стойки переменного сечения на устойчивость следует определять расчетную длину с учетом двух коэффициентов μ. Один из этих коэффициентов характеризует особенности работы стойки в системе рамы. Его назначают по общим правилам и принимают равным 2 при наличии шарнира в верхнем или нижнем узле и 1 при жестком сопряжении стойки с фундаментом и ригелем. Второй коэффициент μ зависит от отношения моментов инерции стойки в местах ее сопряжения с ригелем и фундаментом. Его можно определить по табл. 6.1 [1].

Основные особенности расчета рамы переменного сечения проявляются при ее статическом расчете, поэтому остановимся на этих вопросах подробнее.

Особенности статического расчета рам с элементами переменной жесткости. Известно, что в статически неопределимых системах, в том числе рамных, соотношение жесткостей элементов конструкции влияет на распределение внутренних усилий в ней, что вызывает дополнительные сложности при статическом расчете и подборе сечений элементов.

202

Окончательные размеры сечений устанавливают путем последовательного приближения.

Как правило, все элементы рамных конструкций со сплошной стенкой сжатоизгибаемые. Наиболее распространенной формой сечения является двутавровая. В рамах переменной жесткости чаще всего используют три типа двутавровых сечений: из прокатных двутавров с параллельными гранями полок типа Б с соответствующим переделом; составное из прокатной листовой стали; составное с использованием С-образного холодногнутого профиля в полках и тонкого листового проката в стенке (см. рис. 3.2).

Расчет рам с двутавровыми элементами различных типов сечений до определенной степени идентичен, поэтому ниже рассматривается методика расчета применительно к однопролетной раме переменной жесткости из прокатных двутавров.

Выбор исходного номера двутавра, который принимают в качестве первого приближения, как правило, осуществляют на основе накопленного опыта проектирования с использованием материалов по имеющимся проектам.

Если в вашем распоряжении нет таких проектов, а опыт еще не накоплен, то исходный номер двутавра можно определить в следующем порядке:

1. Приводят нагрузку на ригель рамы к эквивалентной равномерно распределенной q_eq так, чтобы момент в середине пролета шарнирно-опертого ригеля от этой нагрузки q_eql²/8 был равен моменту от веса покрытия с учетом собственного веса ригеля, снегового покрова, кранового и технологического оборудования.
2. Производят статический расчет плоской рамы на эквивалентную нагрузку, условно принимая жесткость рамы постоянной по всему периметру.
3. По изгибающим моментам в карнизе и коньке вычисляют требуемые моменты сопротивления W_req, не обращая пока внимания на влияние продольных сил. Поскольку у развитых двутавров требуемый момент сопротивления выше момента сопротивления исходного двутавра, уменьшают найденные значения W_req в 1,3... 1,5 раза и по сортаменту подбирают исходные номера двутавров типа Б.
4. Из выбранных прокатных балок образуют карнизную и коньковую части рамы путем разрезки (раскроя) стенок профилей по наклонным прямым линиям и последующей сборки (рис. 3.8). При компоновке рамы назначают следующие размеры: Н, L и i - соответственно высоту рамы, пролет и уклон ригеля; с - расстояние от наружной грани стойки до точки на оси ригеля с "нулевым" значением момента; а и b - минимальные высоты сечений полученных элементов; D₁ и D₂ - максимальные высоты сечений элементов.

203

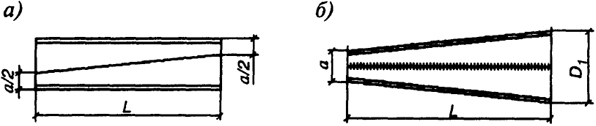Рис. 3.8. Образование элемента переменной жесткости:
а - схема роспуска двутавра; б - элемент переменного сечения

Параметры а и b принимают по конструктивным соображениям и прочностным расчетам. Например, размер а зависит от продольной силы, габаритных размеров оборудования, которое может быть использовано при механизированной резке и сварке, и т.д. Параметр с можно принять по данным расчета рамы с постоянной жесткостью элементов. Размеры D₁ и D₂ определяют из условий прочности сечения и устойчивости стенки (по ее предельно допустимой гибкости). Скомпонованная полурама с основными ее размерами представлена на рис. 3.9. Теперь можно приступать к статическому расчету.

При выполнении статического расчета рамы переменной жесткости возможны два варианта: аналитический (например, с использованием аппарата метода сил) и численный расчет на ЭВМ по стандартным программам.

Особенностью расчета рассматриваемых конструкций является изменение жесткостных характеристик по длине. Для аналитических расчетов необходимо определить функциональную зависимость изменения момента инерции по длине элементов. Изменяющимся параметром у развитого двутавра переменной жесткости по сравнению с исходным является высота стенки элемента. Изменение высоты стенки по длине при прямом резе происходит по линейному закону. Таким образом, определив зависимость момента инерции сечения от высоты стенки, можно определить его распределение по длине элемента конструкции и перейти к расчету рамы с учетом полученных зависимостей. Мы не будем на этом останавливаться, так как в настоящее время предпочтение отдают численным методам.

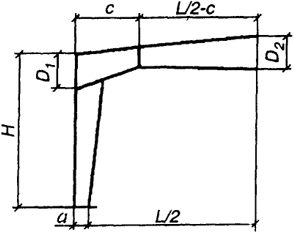Рис. 3.9. Полурама из развитых двутавров переменной жесткости

204

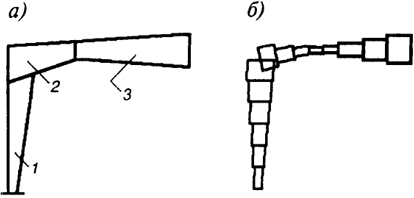Рис. 3.10. К расчетной схеме рамы:
а - исходная полурама; б - аппроксимирующая модель; 1 - стойка; 2 - вут; 3 - ригель

При выполнении численного статического расчета на ЭВМ используют стержневую аппроксимацию элементов рамы. За расчетную принимают ось, проходящую через центры тяжести сечений двутавровых элементов рамы, что обусловливает ее ломаное очертание. Образец расчетной схемы рамы представлен на рис. 3.10.

Каждый элемент рамы (стойка, вут, ригель) разбивают на отдельные участки. Высоту сечения на участке принимают постоянной и равной среднему значению высот на концах участка. Как правило, шаг разбиения рамы на участки длиной 0,5...1 м дает достаточно точные результаты.

Минимальное количество узлов, являющихся границами участков, определяется числом участков согласно шагу разбиения, обязательным введением узла в местах пересечения осей элементов и в местах приложения сосредоточенных нагрузок.

Узлы и стержни элементов удобно нумеровать последовательно, начиная от левой опоры, являющейся одновременно центром координатной системы ZOY.

Исходные данные для расчета на ЭВМ записывают в порядке, установленном для выбранной программы расчета.

Внутренние усилия в раме M, N и Q определяют от каждого вида загружения отдельно. После выполнения статических расчетов на все виды нагрузок составляют таблицу расчетных сочетаний внутренних усилий для характерных сечений подобно тому, как это делалось в гл. 2. По расчетным усилиям производят проверку прочности и устойчивости. Одновременно контролируют величину перемещений в вертикальном и горизонтальном направлениях. В случае невыполнения условий прочности или жесткости выбирают другой номер профиля для элементов рамы, и все операции по расчету повторяют.

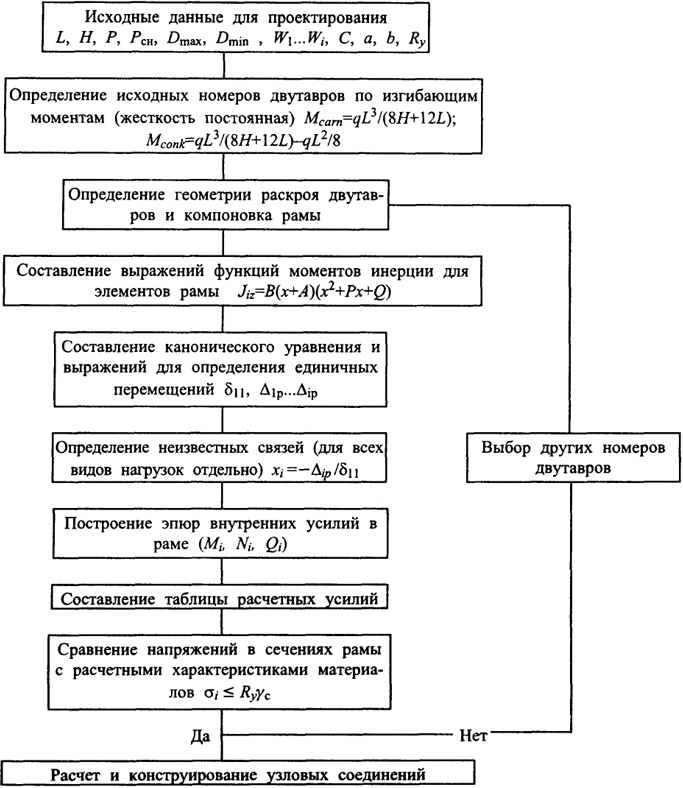
На блок-схеме показана последовательность расчета рамы переменной жесткости методом сил.

205

Схема расчета двухшарнирной рамы переменной жесткости методом сил

206

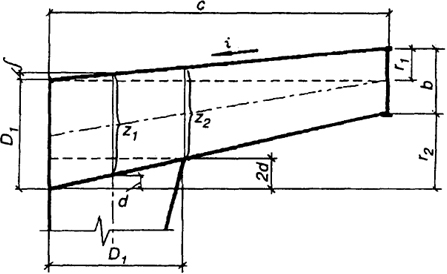Рис. 3.11. Схема карнизного узла

На основании предварительных расчетов по пп.1...3 (см. выше) назначены следующие исходные номера двутавров: стойка - 50Б1; вут - 50Б1; ригель - 45Б1.

Вначале определяем геометрию карнизного узла (рис. 3.11):

D₁ = 734 мм; b = 250 мм; С = 3250 мм; H = 9300 + 150 = 9450 мм; r₁ = ci = 3250 · 0,05 = 162,5 мм; f = D₁r₁ / (2C) = 734 · 162,57 (2 · 250) = 18,5 мм; r₂ = D₁ - b + r₁ = 734 - 250 + 162,5 = 646,5 мм; d = (D₁ r₂) / 2С = (734 · 646,5) / 2 · 3250 = 73,0 мм; z₁ = D₁ + b - d = 734 + 18,5 - 73,0 = 679,5 мм; Н₁ = Н - z₁ / 2 + f = 9450 - 679,5 / 2 + 18,5 = 9128,75 мм; Н₂ = H - D₁ + 2d = 9450 - 734 + 2 · 73,0 = 8862 мм.

Разбиваем все элементы рамы на участки и находим высоты сечений участков (рис.3 Л 2).

Рис. 3.12. К определению высот участков элементов рамы:
1...13 - номера участков

207

Определяем геометрические характеристики сечений по участкам рамы , что удобно осуществлять в табличной форме. В качестве иллюстраций в табл. 3.1 и 3.2 приведены результаты вычислений для стойки и вута из двутавра 50Б1 (S_ч = 860,4 см³, J_ч = 37160 см⁴, A = 92,98 см², t_w = 0,88 см, H = 49,2 см.), при этом использовались следующие формулы: a = 0,5 (H_ish - H_pol); y₁ = (S_x - a²t / 2) / (A / 2).

Определив координаты границ участков и приняв для каждого участка жесткостные характеристики по табл.3.1 и 3.2, можно производить статические расчеты рамы на каждый вид загружения, используя стандартную программу (например, "INTAB", "Ладога", "Лира", "GAMMA", "OSKAR",' "MAK-III", "Рама" и др.).

Таблица 3.1. Геометрические характеристики сечений стойки рамы

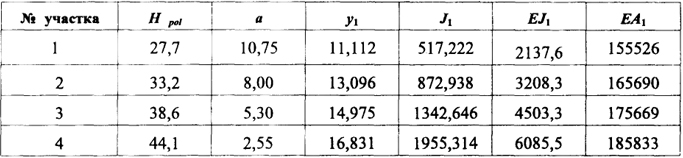
Таблица 3.2. Геометрические характеристики сечений вутовой части

208