Пример 2.12. Рассчитать колонну и разработать ее узлы для бескранового здания по данным примера 2.5.
Расчетные усилия определим по табл.2.5: М = 74,38 кН·м, N = -216,0 кН; материал колонн - сталь С255 с Ry = 24 кН/см2 при t = 10...20 мм; сварка полуавтоматическая - в среде углекислого газа, сварочная проволока - Св-08Г2С.
Определение расчетных длин колонн (рис. 2.48): lef,x = μxН= 2 · 8,55 = 17,1 м; lef,y = μyH = 1 · 8,55 = 8,55 м, где μx = 2 принято по табл. П6.1 или по рис. 6.11 [1].
Подбор сечения колонны. Предварительно зададим высоту сечения колонны h = 300 мм > (1/30) Н. По формулам (6.96) [1] находим
149
 Рис. 2.48. К определению расчетных длин колонны
Рис. 2.48. К определению расчетных длин колонны
λx =
√
=
√
= 4,63;
mef = 1,25
= 1,25
| 74,38 · 102 |
| 216 · 0,35 · 30 |
= 4,1;
φe = 0,160 (табл. П7.1 [1]). Требуемая площадь сечения
Areq =
=
= 56,25 см
2.
По табл.П11.6 [1] принимаем 135ШI с геометрическими характеристиками: A = 83,17 см2, Wx = 1024,4 см3, ix = 14,34 см, iy = 5,84 см, h = 334 мм, tw = 8 мм, bf = 249 мм, tf = 11 мм, Ix = 17108 см4, Iy = 2834,1 см2.
Проверим устойчивость назначенного сечения
λx =
√
=
√
= 4,07;
m =
=
= 2,8.
При Af / Aw = 249· 11/ [(334 - 2 · 11)8] = 1,097 коэффициент влияния формы сечения вычисляем по формуле (см. табл. П8 [1]):
η = (1,90 - 0,1m) - 0,02(6 - m)λx = (1,9 - 0,1 · 2,80) - 0,02(6 - 2,80) · 4,07 = 136;
mef = ηm = 1,36 · 2,8 = 3,81. По табл. П7.1 [1] находим φе = 0,185; N / (φeARyγc)= 216,0 / (0,185 · 83,17 · 24 · 1) = 0,585. Устойчивость колонны в плоскости рамы обеспечена.
Предельная гибкость стержня колонны (см. табл. П9.1[1]) λlim = 180 - 60α = 180 - 60 · 0,585 = 144,9, где α = N / (φеARyγс) = 0,585 < 1. Проверим колонну по предельной гибкости: относительно оси х - λх = lef,x / ix = 17,1 · 102/14,34 = 119,25 < λlim = 144,9; относительно оси у - λу = lеf,y / iy = 8,55 · 102/5,84 = 146,40 > 144,9. Так как гибкость стержня из плоскости рамы больше предельной, принимаем  35Ш2: А = 101,51 см2; Wx = 1275,2 см3; ix = 14,61 см; iy = 6 см; h = 340 мм; tw = 9 мм; bf = 250 мм; tf = 14 мм; Ix = 21678 см4; Iy = 3650,5 см4; It = 0,433 ∑biti3 = 0,433(2 · 25,0 · 1,43 + 32,6 · 0,93) = 69,7 см4 - момент инерции при кручении.
35Ш2: А = 101,51 см2; Wx = 1275,2 см3; ix = 14,61 см; iy = 6 см; h = 340 мм; tw = 9 мм; bf = 250 мм; tf = 14 мм; Ix = 21678 см4; Iy = 3650,5 см4; It = 0,433 ∑biti3 = 0,433(2 · 25,0 · 1,43 + 32,6 · 0,93) = 69,7 см4 - момент инерции при кручении.
Повторяя расчет для нового сечения по прежним формулам, получим λх = lef,x / ix = 117,04 < 151,7; λу = lef,y / iy = 142,5 < 151,7. По гибкости новое сечение удовлетворяет требованиям норм. Понятно, что повторная проверка общей устойчивости этого стержня с большим сечением не требуется.
Проверка устойчивости стержня колонны из плоскости действия момента. Максимальный момент в средней трети сечения колонны (в сечении 3 стержня 3 - 5) Мx = 40,4 кН·м. Дальнейший расчет выполним в последовательности, приведенной в примере 6.13[1],
тх = MxA / (NxWx) = 40,40 · 102 · 101,51 / (203,6 · 275,2) = 1,58; λс = 3,14√E / Ry = 92; φс = 0,598; α = 0,65 + 0,05mх = 0,65 + 0,05 · 1,58 = 0,73; λy = 142,5; φy = 0,305; β = √φс / φу = √0,598 / 0,305 = 1,4; с = β / (1 + αmx) = l ,4 / (1 + 0,73 · 1,58) = 0,65 < cmax = 0,81. Здесь cmax определен по формуле 6.92 [1]:
ρ = (Ix + Iy) / (Ah2) =
| 21678 + 3650,5 |
| 101,51(34,0 - 1,4)2 |
= 0,235;
150
μ = 2 + 0,156Iλy2 / (Ah2) = 2 + 0,156 · 69,7 · 142,52 / (101,51 · 32,62) = 4,05;
δ = 4ρ / μ =
= 0,232;
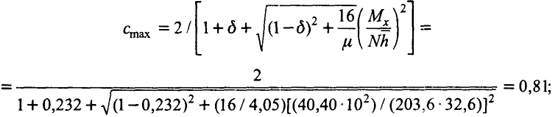
N / (cφyARy) = 216,0 / (0,65 · 0,305 · 101,51 · 24) = 0,447 < 1. Устойчивость обеспечена.
Все проверки выполнены. Однако ввиду того, что жесткости колонн с подобранными сечениями отличаются от заложенных при статических расчетах рамы на 36,7%, что больше 30% , необходимо повторить статические расчеты при фактических жесткостях колонн. Проделав это, можно убедиться, что усилия и моменты практически не изменились (наибольшее отклонение по моментам было в схеме загружения ветровой нагрузкой, которое составило 0,2% от Мmах), поэтому производить корректировку в данном случае не имеет смысла.
Горизонтальные перемещения верхних узлов колонн в плоскости рамы от нормативной ветровой нагрузки увеличились с 17,1 мм (1/500 от Н) до 31,9 мм (1/267 от Н), что также меньше нормативного значения. Представленный анализ позволяет принять окончательное решение о возможности использования I 35Ш2 в качестве стержня колонны.
Расчет базы колонны. Конструкция базы колонны представлена на рис. 2.49. Методика расчета изложена в гл. 6 [I]. Расчетные усилия: М = -74,38 кН·м; N = -216,0 кН. Фундамент из бетона класса В10 с Rb = 0,6 кН/см2 и Rb,lok = φbRb =1,2 · 0,6 = 0,72 кН/см2.
Назначаем ширину опорной плиты В = 40 см; при этом ее длина
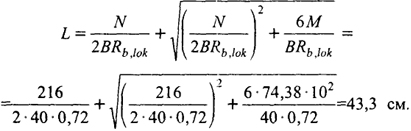
Принимаем опорную плиту с размерами в плане 400 × 500 мм; размеры верхнего уступа фундамента устанавливаем 540 × 640 мм, что соответствует φb = 1,2.
Краевые напряжения в бетоне фундамента (рис. 2.49, б)
σmax =
+
=
-
= 0,34 кН/см
2 .
Положение нулевой точки в эпюре напряжений x = σmin L / (σmax + σmin) = 0,34 · 50 / (0,55 + 0,34) = 19,1 см. Напряжения на участке сжатия эпюры напряжений σ1 = σmax × 21,5 / 30,9 = 0,55 · 21,5 / 30,9 = 0,38 кН/см2; σ2 = σmах · 22,9 / 30,9 = 0,55 · 22,9 /30,9 = 0,41 кН/см2.
Определяем толщину опорной плиты.
Участок 1 (рис. 2.49, а). Изгибающий момент M1 = σmax А1С1 = 0,55 · 315 · 4 = 693 кН·см, где А1 = (34 + 50)0,5 · 7,5 = 315 см2 - площадь трапеции условного консольного участка плиты; С1 = 4 см - расстояние от центра тяжести трапеции до условной опорной кромки плиты:
С1 =
=
| 34 · 0,5 · 7,5 + 2 · 0,5 · 8 · 7,5 · 2 / 3 · 7,5 |
| 315 |
= 4 см.
151
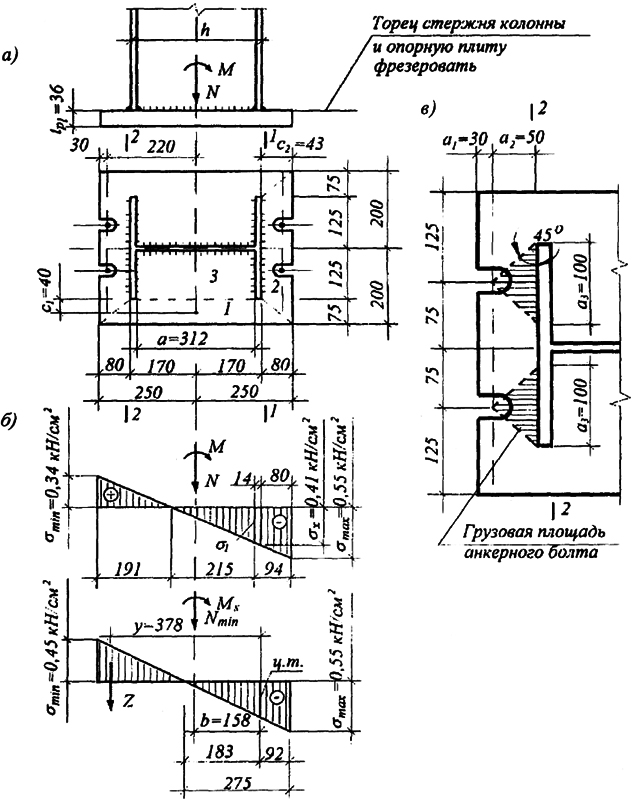 Рис. 2.49. База колонны бескранового здания:а
Рис. 2.49. База колонны бескранового здания:а - конструкция базы;
б - эпюры напряжений;
в - к проверке прочности плиты
Толщина опорной плиты (сталь С255 при t > 20 мм , Ry = 23 кН/см2)
tpl,1 = √
= √
= 2,10 см.
Участок 2. М2 = σтах · А2С2 = 0,55 · 260 · 4,3 = 614,9 кН·см; A2 = (25 + 40)0,5 · 8,0 = 260 см2;
C2 =
| 25 · 8,0 · 0,5 · 8,0 + 2 · 7,5 · 8,0 · 0,5 · 2 / 3 · 8 |
| 260 |
= 4,3 см;
152
tpl,2 = √6M2 / (bfRyγc) = √6 · 14,9 / (25 · 23 · 1,2) = 2,31 см.
Участок 3. Изгибающий момент в пластинке, опертой на три канта М3 = βσ1a2 = 0,060 · 0,38 · 31,22 = 22,2 кН·см; коэффициент β определен по табл. 6.9 [I], а = 31,2 см - длина свободной стороны пластинки.
Толщина плиты
tpl,3 = √6M3 / (1 ̭ Ryγc) = √6 · 22,2 / (1 · 23 · 1,2) = 2,2 см.
Принимаем толщину опорной плиты tpl = 2,5 см.
Проверяем прочность опорной плиты в сечении 1 - 1:
σx = M1-1 / Wpl = 6M1-1 / (Btpl2) = 6 · 704 / (40 · 2,52) = 16,9 кН/см2; τxy = Q1-1 / (Btpl) = 176 / (40 · 2,5) = 1,76 кН/см2; здесь Q1-1 = σmax S = 0,55 · 40 · 8 = 176 кН; M1-1 = 176 · 8/2 = 704 кН·см; σred = √σx2 + 3τxy2 = √16,92 + 3 · 1,762 = 17,2 кН/см2 < 1,15 Ryγc = 26,45 кН /см2.
Расчет анкерных болтов. Анкерная комбинация усилий: Nmin = -95 кН; Ms = 83,14 кН·м. Краевые напряжения в бетоне фундамента при этой комбинации усилий (рис. 2.49, б): σmax =
-
=
-
= - 0,55 кН/см
2;
σmin = - 0,45 кН/см
2.
Положение нулевой точки на эпюре напряжений
x = σmaxL / (σmax + σmin) = 0,55 · 50 / (0,55 + 0,45) = 27,5 см.
Растягивающее усилие в анкерных болтах
Z = (Ms - Nminb) / y = (83,14 · 102 - 95 · 15,8) / 37,8 = 180,2 кН.
На один анкерный болт приходится усилие 90,1 кН. По табл.6. 1 1[1] назначаем анкерные. болты типа 1 диаметром 36 мм с глубиной заделки в фундаменте 1300 мм.
Проверка приведенных напряжений в плите в зоне действия анкерных болтов по сечению 2 - 2 (рис. 2.49, в):
σx = M2-2 / Wp,2-2 = 6M2-2 / (2a3tpl2) = 6 · 901 / (2 · 10,0 · 2,52)= 43,2 кН/см2 > Ryγc = 23 кН/см2; τxy = Q2-2 (2a3tpl) = 180,2 / (2 · 10 · 2,5) = 3,6 кН/см2; Q2-2 = Z = 180,2 кН; М2-2 = Q2-2 a = 180,2 · 5 = 901 кН·см.
Так как σх > Ry γc, увеличиваем толщину плиты до 36 мм. При этом
σx = 6М2-2 / (2а3 tpl2) = 6 · 901 / (2 · 10 · 3,62) = 20,9 кН/см2 < Ry γс = 23 кН/см2;
τxy = Q2-2 / (2a3 tpl) = 180,2 / (2 · 10 · 3,6) = 2,5 кН/см2;
σred = √σx2 + 3τxy2 = √20,92 + 3 · 2,52 = 21,3 кН/см2 < 1,15 Ry γc = 26,45 кН/см2. Прочность сечения 2 - 2 обеспечена.
Расчет оголовка колонны. Схема оголовка представлена на рис. 2.50. К оголовку приложена сила F = 227,1 кН.
Толщину и размеры в плане опорной плиты назначаем конструктивно (см.п.6.8.1[1]): t = 16 мм; b × l = 280 × 370 мм. Плиту соединяем со стержнем колонны с помощью угловых сварных швов с минимальным катетом kf = 6 мм (табл. 4.5 [1]). Общую ширину опорных ребер принимаем равной ширине опорного фланца фермы br = 18 см. Из условия смятия толщина ребра tr = 1,2F / (brRp) = 1,2 · 227,1 / (18 · 36) = 0,42 мм. Здесь Rp = 36 кН/см2 для стали С255, коэффициент 1,2 учитывает возможный перекос опорного фланца фермы. Принимаем tr = 6 мм.
Длину опорных ребер вычислим из условия размещения сварных швов, крепящих их к стенке колонны (kf = 6 мм; βf = 0,9; βz = 1,05; Rwf = 21,5 кН/см2; Rwz = 0,45; Run = 0,45 · 37,0 = 16,65 кН/см2). Поскольку βfRwz = 1,05 · 16,65 = 17,5 кН/см2 < βfRwf = 0,9 · 21,5= 19,3 кН/см2 расчет выполняем по границе сплавления
153
lwz =
=
| 1,2 · 227,1 |
| 4 · 1,05 · 0,6 · 16,65 · 1 · 1 |
= 6,5 см.
Принимаем по конструктивным соображениям длину ребра lr = 20 см.
Проверка прочности стенки на срез по граням крепления опорных ребер: N / (2lrtw) = 227,1 / (2 · 20 · 0,9) = 6,3 кН/см2 < Rs γс = 14 кН/см2.
Прочность обеспечена.
Пример 2.13. Выполнить расчет и конструирование колонны по данным примера 2.6. Конструктивная схема и ее размеры приведены на рис. 2.51. Расчетные усилия в сечении 1 (см. рис. 2.20) М = - 172,9 кН·м, N = - 298,7 кН.
Определение расчетных длин колонны. Ввиду того, что в точке 5 (см. рис. 2.20) на стержень колонны передается большая по величине сосредоточенная сила от вертикальных крановых воздействий, будем определять расчетные длины колонн отдельно для подкрановой и надкрановой частей. При этом воспользуемся табличными решениями табл. П6.2.
Расчетные длины колонны в плоскости рамы. Коэффициенты расчетной длины μ1 и μ2 определим в зависимости от параметров n = I2l1 / I1l2 = l1 / l2 = 7330 / 3020 = 2,43 и
α1 = l2√I1 / (I2β) / l1 = l2√1 / β / l1 = 3020√1 / 2,08 / 7330 = 0,29,
где β = (F1+ F2) / F2 = 376,3 / 181,0 = 2,08 (F1 + F2 - наибольшее значение продольной силы в подкрановой части колонны при воздействиях 1, 2, 3; F1 - значение продольной силы в надкрановой части при том же загружении рамы); I1 = I2.
Принимая верхний конец колонны (для однопролетной рамы с шарнирным сопряжением ригеля и стойки) свободным по табл. 67 [6], находим μ1 = 2,46; μ2 = μ1/α1 = 2,46/0,29 = 8,48 > 3, назначаем μ2 = 3, тогда расчетные длины будут равны:
- для подкрановой части lef,x1 = μ1l1 = -2,46 · 7,33 = 18,03 м;
- для надкрановой части lef,x2 = μ2l2 = 3 · 3,02 = 9,06 м.
Расчетные длины колонны из плоскости рамы: lef,y1 = 7,33 м; lef,y2 = 3,02 м.
Подбор сечения колонны. Проектирование колонны выполняем в соответствии с рекомендациями п.6.7.7 [1]. Высоту сечения назначаем из условия жесткости с учетом принятого
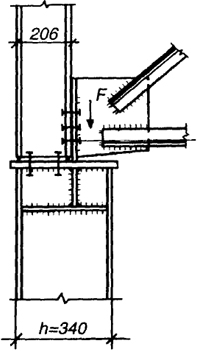 Рис. 2.50. Конструктивная схема оголовка
Рис. 2.50. Конструктивная схема оголовка
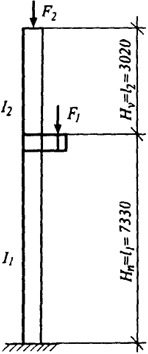 Рис. 2.51. К определению расчетных длин колонны
Рис. 2.51. К определению расчетных длин колонны
154
при статическом расчете рамы значения h = 1/20l = 44 см. По формулам (6.96) [1] находим:
λx = lef,x1√Ry / E / (0,42h) = 18,03 · 102√24 / (2,06 · 104) / (0,42 · 44) = 3,33; mef,x = 1,25 · M / (N × 0,35h) = 1,25 · 172,9 · 102 / (298,7 · 0,35 · 44) = 4,7; e = 0,185; Atr = N / ( eRy c) = 298,7 / (0,185 · 24 · 1) = 67,3 см2.
По табл. П11.6 [1] принимаем I 45Ш1 с геометрическими характеристиками сечения: А = 157,38 см2; Wx = 2548,7 см3; Ix = 56072 см4; Iу = 8110,3 см4; ix = 18,88 см; iy = 7,18 см; h = 440 мм; bf = 300 мм; tw = 11 мм; tf = 18 мм.
Проверка устойчивости колонны в плоскости рамы:
x = lef,x1 / ix = 18,03 · 102 /18,88 = 96,6; λx = 3,3; Af / Aw = 300 · 18 / [(440 - 2 &3183; 18)11] = 1,22; η = (1,90 - 0,lm) - 0,02(6 - m)λx = (1,90 - 0,1 · 3,57) - 0,02(6 - 3,57) · 3,3 = 1,38; т = MA / (NWx) = 172,9 · 102 · 157,38 / (298,7 · 2548,7) = 3,57; mef = m = 1,38 · 3,57 =4 ,93; e = 0,182; = N /( eA) = 298,7 / (0,182 · 157,38) = 10,43 кН/см2 < Ry c = 24 кН/см2. Устойчивость колонны в плоскости рамы обеспечена с большим запасом, но уменьшить ее сечение мы не можем по условию жесткости.
Гибкость колонны х = 96,6 и у = lef,yl1 / iy = 7,33 · 102 / 7,16 = 102,3 не превышает предельного значения ( х < lim и y < lim), где lim = 180 - 60 = 180 - 60 · 0,43 = 154,2; = N / ( eARy c)= 298,7 / (0,182 · 157,38 · 24 · 1) = 0,43.
Проверка устойчивости стержня колонны из плоскости рамы. Предварительно находим сmах по формуле (6.92) [1]:
= 4 / = 4 · 0,23 / 3,02 = 0,3;
ρ = (Ix + Iy) / (Ah2) = (56072 + 8110,3) / [157,38(44 - 1,8)] = 0,23;
μ = 2 + 0,156
λy2 = 2 + 0,156
120,3
2 = 3,02;
It = 0,433 ∑ bi ti3 = 0,433[2 · 30 · 1,83 + (44 - 2 · 1,8)1,13] = 174,8 см4;

Проверяем устойчивость по формуле (6.90) [1]:
= N / (c у A) = 298,7 / (0,374 · 0,527 · 157,38) = 9,6 кН/см2 < Rу с = 24 кН/см2.
Здесь у = 0,527 по приложению 6 [1] при y = 102,3; с = / (1+ mx)=1,07 / (1 + 0,77 · 2,42) = 0,374 < сmах = 0,559. При определении коэффициента с использованы следующие соотношения:
тх = MxA / (NxWx) = 117,2 · 102 · 157,38 / (298,7 · 2548,7) = 2,42,
где
β = √φc / φy = √0,598 / 0,527 = 1,07; c = 0,598 при
155
λс = 3,14√E / Ry = 3,14√2,06 · 104 / 24 = 92; α = 0,65 + 0,05mх =0,65 + 0,05 · 2,42 = 0,77.
Расчет базы колонны. Конструкция базы колонны представлена на рис. 2.52, а. Материал фундамента - бетон класса В10, Rb = 0,6 кН/см2. При φb = 1,3 Rb,lok = φb Rb =1,3 · 0,6 = 0,78 кН/см2.
Определение размеров опорной плиты в плане. Ширина опорной плиты В = bf + 2(ttr + c) = 30,0 + 2(l + 6,5) = 45 см, где bf = 30 см - ширина полки колонны; ttr = 1 см - толщина траверсы; с = 6,5 см - вылет консольной части плиты. Длину плиты находим по формуле (6.108) [1]:

Принимаем плиту с размерами в плане 450 × 600 мм; размеры верхнего обреза фундамента устанавливаем 700 × 850 мм. При этом b = 1,301.
Определение толщины опорной плиты. Краевые напряжения в бетоне фундамента под опорной плитой
σmax =
+
= -
-
= - 0,111 - 0,64 = - 0,75 кН/см
2;
σmin = - 0,111 + 0,64 = 0,53 кН/см2. Эпюра напряжений показана на рис. 2.52, б, в.
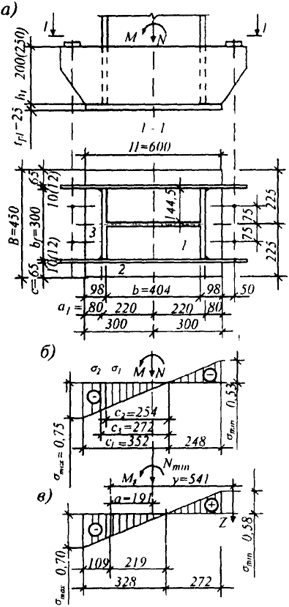 Рис. 2.52. К расчету базы колонны
Рис. 2.52. К расчету базы колонны
Изгибающие моменты в опорной плите: на участке 1, опертом на 4 канта: b/а = 404/144,5 = 2,8 >2, следовательно, по табл. 6.8 [1] α1 = 0,125 и M1 = α1σ1 a2 = 0,125 · 0,54 · 14,452 = 14,1 кН·см; на консольном участке 2: M2 = σmах · С2 / 2 = 0,75 · 6,52 / 2 = 15,8 кН·см; на участке 3, опертом на 3 канта: а1/b1 = 80/300 = 0,27 < 0,5, момент определяем как для консольного участка с вылетом консоли а1М3 = σmах · a12 / 2 = 0,75 · 8,02 /2 = 24,0 кН·см. Толщину опорной плиты находим по максимальному моменту
tpl = √6Mmax / (Ryγc) = √6 · 24,0 / (24 · 1,2) = 2,24
см. Принимаем tpl = 25 мм.
Расчет траверсы. Траверсу в расчетной схеме представляем двухконсольной балкой (рис. 2.53), шарнирно опертой на пояса колонны. В качестве нагрузки принимаем в сжатой зоне под плитой отпор (давление) со стороны фундамента,
156
собранный с грузовой площади (на одну траверсу с половины ширины плиты) qtr,max = σmax B/2 = 0,75/22,5 = 16,875 кН/см; в растянутой зоне - усилия в анкерных болтах
Za
=
| 17290 - 298,7 · 18,3 |
| 2 · 53,3 |
= 110,92 кН.
Эпюры моментов и перерезывающих сил от указанных нагрузок представлены на рис. 2.53. Из этих эпюр следует, что в качестве расчетных сечений траверсы следует выделить сечения I и II. Здесь: М1 = 15,42 кН·м и Q1 = 110,9 кН; Q2 = 182,6 кН и VA = 313,8 кН. По моменту в сечении I определяем
Wtr,req =
=
= 64,25 см
3.
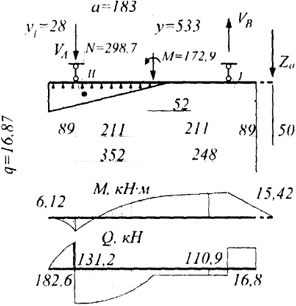 Рис. 2.53. Расчетная схема траверсы базы колонны
Рис. 2.53. Расчетная схема траверсы базы колонны
При ttr = 10 мм htr = √64,25 · 6 = 19,63 см. Принимаем htr = 20 см. Проверяем принятое сечение траверсы на срез по QII = 182,6 кН
τ =
=
= 13,7 < 0,58 · 24 = 13,92 кН/см
2.
Расчет шва, соединяющего траверсу со стержнем колонны, из условий восприятия реакции VA = 313,8 кН. По табл. 34*[7] принимаем βf = 0,8; Rwf =21,5; βz = 1; Rwz= 16,65. Так как βfRwf > βzRwz расчет проводим по металлу границы сплавления. Требуемый катет шва
kf = VA / (βz Rwz γwz γc lw) = 313,8 / (1 · 16,65 · 1 · 1 · 19) = 0,99 см.
Принимаем kf = 10 мм.
Торец колонны (после приварки траверс) и плиту фрезеруем. В этом случае швы приварки к плите назначают конструктивно минимальной высоты. При толщине плиты 25 мм по табл.4.5 [1] принимаем высоту катета 7 мм.
Расчет анкерных болтов. По данным примера 2.6 Nmin = - 173,0 кН; Ms = - 172,7 кН м. При этой комбинации
σmax =
+
= -
-
= - 0,70 кН/см
2.
σmin = 0,58 кН/см2. Эпюра напряжений показана на рис.2.52, в. Растягивающее усилие в одном анкерном болте Z = (Ms - Nmin a) / 2y = (172,7 · 102 - 173,0 · 19,1) / (54,1 · 2) = 129,07 кН. По табл. 6.11 [1] принимаем болты диаметром 42 мм с заделкой типа 3 глубиной 700 мм.
Проверка прочности траверсы на усилия в анкерных болтах показывает, что ее прочность не обеспечена, поэтому увеличим размеры траверсы htr =25 см; ttr = 1,2 см и повторим проверку. Усилия в анкерных болтах Qtr= Z = 129,07 кН; Mtr = Zl = 129,07(8 + 5) = 1677,9 кН·см;
σx = 6Mtr / (ttrhtr2) = 6 · 1677,9 / (1,2 · 252) = 13,42 кН/см2 < Ryγc = 24 кН/см2;
τxy = 1,5Qtr / (ttrhtr) = 1,5 · 129,07 / (1,2 · 25) = 6,45 кН/см2 < Rsγс = 19,92 кН/см2.
Прочность траверсы обеспечена. Измененные размеры траверсы на рис. 2.52 указаны в скобках.
В связи с тем, что в конструкцию базы потребовалось ввести траверсу (ht = 25 см), изменяем величину заглубления опорной плиты до отметки - 0,400 м. При этом следует скорректировать высоту колонны, приняв ее равной H = Ho + H1 = 10200 + 400 = 10600 мм.
157
Проверка прочности подкрановой консоли (рис. 2.54). Расчетные усилия в заделке консоли Q = F = N3 + Dmax = 18,66 + 174,85 = 193,51 кН; М = F lc =193,51 · 31,0 = 6000 кН·см. Принимаем для консоли I 30Ш1: А = 291 мм; bf = 200 мм; tf = 11 мм; tw = 8 мм; Ix = 10400 см4; Wx = 715 см3; Sx = 398 см3. Расчет производим в соответствии с п.6.8.2[1].
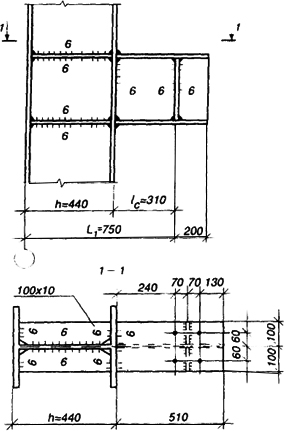 Рис. 2.54. Подкрановая консоль
Рис. 2.54. Подкрановая консоль
Напряжения в консоли: σх = M / W* = 6000 / 715 = 8,4 кН/см2 < 24 кН/см2; τху = Q Sx / (tw Ix) = 193,51 · 398 / (0,8 · 10400) = 9,3 кН/см2 < 13,92 кН/см2.
Так как напряжения в консоли много меньше расчетных сопротивлений, проверку по приведенным напряжениям не проводим.
Сварные швы крепления консоли к полке колонны проверим в предположении, что изгибающий момент воспринимается только полками, а поперечная сила - стенкой (п.6.8.2 [1])
H = M / hc = 6000 / (29,1 · 1,1) = 214 кН; Q = 193,51.
Принимаем все швы с катетом 6 мм. Сварка полуавтоматическая проволокой 08 Г2С; βf = 0,9; βz = 1,05; Rwf = 21,5 кН/см2; Rwz = 16,65 кН/см2. Поскольку βfRwf βzRwz, расчет швов выполняем по металлу границы сплавления:
H / (2βzkflwRwzγwzγc) = 214 / [2 ·1,05 · 0,6 (20 - 1) 16,65] = 0,54 < 1;
Q / (2βzkflwRwzγwzγc) = 0,34 < 1.
Прочность швов обеспечена.
Стенку колонны в месте примыкания подкрановой консоли укрепляем парными поперечными ребрами жесткости из листов 100 ×10 мм.
Проверим прочность швов крепления ребер к полке колонны: расчетная длина шва lw = 2(br - 3 - 1) = 2(10 - 3 - 1) = 12 см. Здесь 3 см - размер выреза в ребре. Прочность шва обеспечена, так как H / (2βzkflwRwzγwzγc) = 214 / [2 · l,05 · 0,6 · 12 · 16,65] = 0,85 < 1.
В зоне крепления верхнего пояса консоли к колонне в полке колонны возникают растягивающие напряжения, направленные перпендикулярно плоскости полки, равные H / (bctef), где tef = tf + 2kf, tf и bc - толщина и ширина пояса консоли. Прочность полки колонны обеспечена, поскольку H / (bctefRth) = 214 / (20 · 2,3 · 180) = 0,23 < 1 . Здесь Rth = 0,5 Ru = 0,5 · 36 = 18кН/см2 - расчетное сопротивление стали С255 в направлении толщины проката.
Усилие H передается с ребер на стенку колонны. Проверим прочность швов крепления ребер к стенке колонны. Расчетная длина швов lw = h - 2tf - 2 · 3 = 44 - 2 · 1,8 - 6 = 34,4 см (h и tf - высота сечения и толщина полки колонны, 3 см - вырез в ребре);
H / (4βzkflwRwzγwzγc) = 214 / [4 · l,05 · 0,6 · 34,4 · 16,65] = 0,15 < 1.
Прочность швов обеспечена.
Проверка прочности стенки колонны на срез по граням крепления ребер:
H / (2lrtwRs) = 214,2 / (2 · 34,4 · 1,1 · 0,58 · 24) = 0,2 < 1.
158
Прочность стенки на срез обеспечена.
В стенке колонны на участке между ребрами помимо усилий М, N и Q, определенных при расчете рамы в сечении 5 элемента 5 - 9, действуют усилия Н. Проверим прочность стенки колонны по приведенным напряжениям в месте примыкания консоли (М = -57,3 кН·м, N = -200,2 кН, Q = -19,13 кН)
= Mhw / (2Ix) + N/A = 57,3 · 102 (440 - 2 · 1,8) / (2 · 56072) + 20,2/157,38 = 2,19 кН/см2;
= (Q + H) / (tw hw) = (19,13 + 214,2) / [1,1 (44 - 2 · 1,8)] = 5,25 кН/см2;
σred = √σ2 + 3τ2 = √2,192 + 3 · 5,252 = 9,35 кН/см ≤
Таким образом прочность узла обеспечена.
Пример 2.14. Запроектировать ступенчатую колонну по данным примера 2.7.
Надкрановую часть будем проектировать из прокатного профиля, подкрановую - составной, сплошностенчатой. Материал колонны - сталь С225 с Ry = 24 кН/см2 при t = 10...20 мм и Ry = 23 кН/см2 при t ≥ 20 мм. Сварка элементов - автоматическая и полуавтоматическая в среде углекислого газа; сварочная проволока Св-08Г2С.
Расчетные усилия примем по табл. 2.11. Для надкрановой части в сечении 11 (9 - 11) (см. рис. 2.23, б) N1 = -531,4 кН, M1 = 573,9 кН·м.
Для подкрановой части сечение 1(1 - 3) - N2 = -2141,6 кН, M2 = -789,2 кН·м (момент догружает наружную ветвь), Q = -143,4 кН; N3 = -1872,1; М3 = 696,4 (момент догружает подкрановую ветвь), Q3 = 25,9 кН. Соотношение жесткостей надкрановой и подкрановой частей колонны, принятое при расчете рамы, EIv / EIn = 0,17.
Определение расчетных длин колонны в плоскости рамы. Подкрановая часть - lef,x1 = 1l1 (l1 = Нn); надкрановая - lef,x2 = 2l2 (l2 = Hv). Коэффициенты расчетной длины 1 и 2 определим по табл. П6.3 в зависимости от параметров:
n =
=
= 0,26 и
α1 =
√
=
√
= 0,8
где I2 = Iv, I1 = In; = (F1 + F2) / F2 = 2104,58 / 522,94 = 4,03; (F1+F2 = Nmax,5(3-6) - наибольшее значение продольной силы в т. 6 подкрановой части колонны при сочетаниях 1, 2, 3, 6, 8; F2 - значение продольной силы в т. 11 надкрановой части колонны при тех же сочетаниях нагрузок). В рассматриваемой раме верхний конец колонны закреплен только от поворота. По табл. П6.3 1 = 1,93, 2 = 1 / 1 = 1,93 / 0,8 = 2,4 < 3; lef,x1= 1,93 · 9 = 17,37м; lef,x2 = 6,0 · 2,4 = 14,4 м.
Расчетные длины из плоскости рамы принимаем равными геометрическим в пределах участков между связями из плоскости рамы. Для надкрановой части lеf,y2 = 6,0 - 1,65 = 4,35 м (1,65 м - высота подкрановой балки на опоре). Для подкрановой части при наличии распорок между колоннами в середине их длин lef,y1 = 0,5 · 9,0 = 4,5 м.
Подбор сечения надкрановой части колонны. Надкрановую часть колонны проектируем из широкополочного двутавра. Расчет выполняем по аналогии с примером 6.13 [1]. Требуемая площадь сечения надкрановой части колонны при заданной высоте сечения hv = 50 см равна: A = N1 / ( e Ry с) = 531,4 / (0,152 · 24 · 1) = 145,6 см2, где е = 0,152 при mef = 1,25M1 / (N1 · 0,35h) = 1,25 · 572,9 · 102 / (531,4 · 0,35 · 50) = 7,7 и λх = lef,x2√Ry / E / (0,42h) = 14,4 · 102√24 / (2,06 · 104) / (0,42 · 50) = 2,3. По табл. П11.5[1] подбираем двутавр 50Ш2 (попытка принять двутавр 50Ш1 не увенчалась успехом, так как он не прошел по устойчивости) с характеристиками : А = 176,6 см2, Ix = 75530 см4, Wx = 2967 см3, ix = 20,26 см, iy = 6,69 см, h = 489 мм, tw = 14,5 мм, bf = 300 мм, tf = 17,5 мм.
159
Определяем гибкости стержня надкрановой части колонны в плоскости и из плоскости рамы: λx = lef,x2 / ix = 14,4 · 102 / 20,26 = 71,7 < llim = 126; λх =2,43; λу = lef,y2 / iу = 4,35 · 102 / 6,69 = 65; λy = 2,22.
Предельная гибкость λlim 180 - 60α = 180 - 60 · 0,9 = 126, где α = N1 / (φе ARyγc) = 531,4 / (0,139 · 176,6 · 24 · 1) = 0,9. Здесь φе = 0,139 (табл. П7.1 [1]) при λx = 2,43; и mef = 8,4. mef = ηт = 1,31 · 6,4 = 8,4, где η = 1,31 (табл. П.8 [1]) при Af / Aw = (30 · 1,75) / [(48,9 - 2 · 1,75) · 1,45] = 0,8 и m = M1A / (N1Wx)= 572,9 · 102 · 176,6 / (531,4 · 2967) = 6,4.
Проверка устойчивости стержня колонны в плоскости действия момента: σ = N1 / (φe A × Ryγc) = 531,4 / (0,139 · 176,6 · 24) = 0,9 < 1.
Проверка устойчивости стержня колонны из плоскости действия момента σ = N1 / (cφy A × Ryγc) = 531,4 / (0,197 · 0,780 · 176,6 · 24) = 0,82 < 1. Здесь φу = 0,780; с = 0,197. Коэффициент с вычислен в зависимости от значения относительного эксцентриситета
mx =
=
| 413,05 · 176,6 |
| 531,4 · 2967 |
= 4,63,
где Мх = 2/3 (573,9 - 93,35) + 93,35 = 413,05 кН·м (93,35 кН·м - момент в сечении 9 элемента 9-11 надкрановой части колонны, вычисленный при том же сочетании нагрузок, что и М = 573,9 кН·м). с = β / (1 + αтх) = 17 (1 + 0,88 · 4,63) = 0,197. При α = 0,65 + 0,05 тх = 0,65 + 0,05 · 4,63 = 0,88, β = 1, так как
λу = 65 < λС = 3,14√E / Ry = 3,14√2,06 · 104 / 24 = 92
Подбор сечения подкрановой части колонны. Для подкрановой части принимаем сплошное составное сечение с подкрановой ветвью из прокатного двутавра и наружной полкой из листа. Высота сечения колонны (расстояние от наружной грани до оси подкрановой ветви) h = 1000 мм (рис. 2.55). Для двутаврового сечения rх 0,42h; ρч 0,35h. Тогда
λx = (lef,x1 / 0,42h)√Ry / Е = (1737 / 0,42 · 100)√24 / 2,06 · 104 = 1,4;
mх = M2 / (N2 / ρx) = 78920 / (2141,6 · 0,35 · 100) = 1,05. В первом приближении принимаем η = 1,5 (для двутавра η 1,2...1,7); mef = mхη = 1,05 · 1,5 = 1,58. По табл. П7Л [1] φе = 0,51. Требуемая площадь сечения по формуле (6.85) [1]
Areq = N2 / (φе Ry γс) = 2141,6 / (0,51 · 24 · 1) = 175 см2 .
Компоновка сечения. Высота стенки hw h - tf = 100 - 2 = 98 см (предварительно принимаем tf =2 см). Предельная гибкость стенки (табл. 27* [7]) при λ < 2 λuw = 1,3 + 0,15 · 1,42 = 1,3 + 0,15 · 1,42 = 1,59. Из условия местной устойчивости стенки λw = (hw / tw)√Ry / E) ≥ λuw = 1,59. Тогда tw ≤ (hw / λuw)√Ry / E = (98 / 1,59)2√4 / 2,06 · 104 = 2,1 см. Поскольку сечение со столь толстой стенкой не экономично, принимаем tw = 8 мм (hw / tw = 80...120), предполагая при этом, что стенка потеряет местную устойчивость (см. рис. 6.18 [1]), и включаем в расчетную площадь сечения колонны два крайних участка стенки шириной h1 ≈ 0,4twλuw√E / Ry = 0,4 · 0,8 · 1,59√2,06 · 104 / 24 = 15 см. Требуемая суммарная площадь полок равна: Areq-2twh1 = 175 - 2 · 15 · 0,8 = 151 см2. Принимаем подкрановую ветвь из 140Б1 (табл. П11.6 [1]) с геометрическими характеристиками: A = 72,16 см2; Jx = 20020 см4; iх = 16,66 см; Jy = 1446,9см4; tw = 1 мм; tf = 11 мм; bf = 199 мм.
160
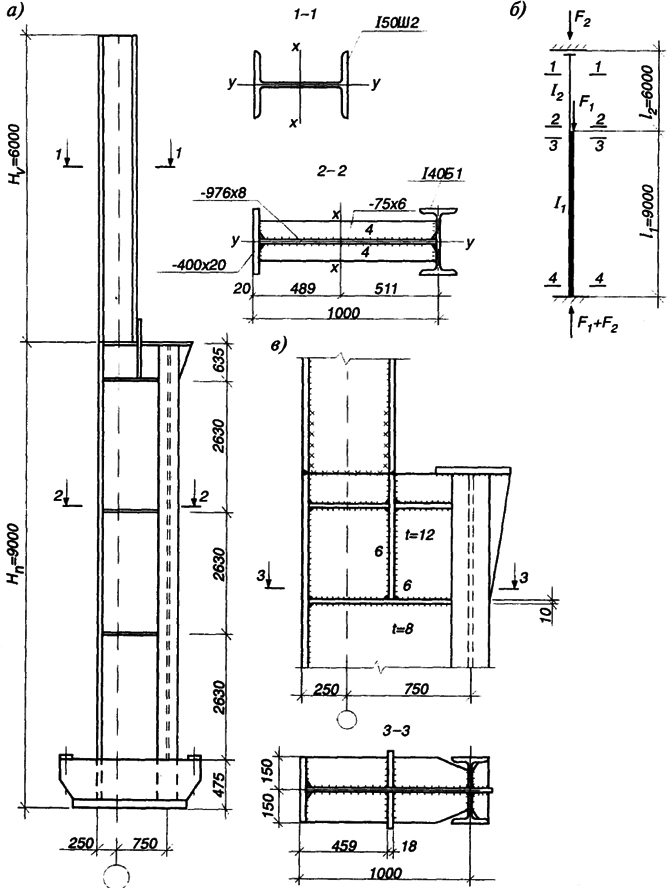 Рис. 2.55. К примеру 2.14
Рис. 2.55. К примеру 2.14
161
Для наружной полки принимаем лист 20 × 400 мм. Местная устойчивость полки обеспечена, так как bef / tf = (40 - 0,8) / (2 · 2) = 9,8 < (0,36 + 0,1λ)√E / Ry = (0,36 + 0,1 · 1,4) × √2,06 · 104 / 24 = 14,6 (6.38 [1]).
Геометрические характеристики принятого сечения: hw = 97,65 см; A =230,3 см2; расстояние от наружной грани колонны до центра тяжести у = 48,9 см; Jx = 435700 см4; ix = 43,5 см; моменты сопротивления для наружной полки Wx1 = 8910 см3; для подкрановой ветви Wx2 = 7140 см3; ядровые расстояния ρх1 = 38,7 см; ρх2 =31 см; Jt = 30690 см4; iy = 11,5 см; λx = 40; λx = 1,37; λy = 39.
Поскольку ранее принятое значение λx = 1,4 почти не отличается от полученного значения, предельная гибкость стенки не изменится и значение h1 останется прежним.
Расчетная площадь сечения с учетом исключения из работы части стенки составляет Ared = 80 + 72,16 + 0,8 · 15 · 2 = 176,16 см2.
Проверим устойчивость подкрановой части колонны в плоскости рамы на две комбинации усилий (см. исходные данные).
Первая комбинация (момент догружает наружную полку): mx = M2 / (N2 ρx1) = 78920 / (2141,6 · 38,7) = 0,95. Значение η определяем по табл.П8 [1] для типа сечения 2: Af1 / Aw 1; при т < 5 η = (1,9 - 0,1 · 0,95) - 0,02(6 - 0,95)1,37 = 1,66; mef = 1,66 · 0,95 = 1,58. По табл.П7.1 [1] φе = 0,51 N2 / (φeARy) = 2141,6 / (0,51 · 24 · 176,16) = 0,99 < 1. Устойчивость обеспечена.
Вторая комбинация (момент догружает подкрановую ветвь): тх = M3 / (N3ρx2) = 69640 / (1872 · 31) = 1,2; Аf2 / Aw = 0,92. Значение η определяем по табл.П8[1] для типа сечения 4. Выполнив интерполяцию между значениями η при Af2 / Aw = 1 и Af2 / Aw = 0,5, получим η =1,62; mef = 1,94; φе = 0,458; N3 / (φeARy) = 1872 / (0,458 · 24 · 176,16) = 0,95 < 1. Устойчивость обеспечена.
Проверка устойчивости из плоскости рамы. Максимальный момент в средней трети подкрановой части Мх = 2/3 (789,2 - 153,87) + 153,87 = 577,42 (153,87 кН·м - момент в сечении 3 элемента 1 - 3, вычисленный при том же сочетании нагрузок, что и М = 789,2 кН·м в сечении 1), mx = Mx / (N2 ρx1) = 57742 / (2141,6 · 38,7) = 0,69; по п.5.31 [7] при тх < 5 с = β / (1 + αтx) = 1 / (1 + 0,7 · 0,69) = 0,67. Здесь α = 0,7; β = 1 (табл. 10 [7]). По табл.П6[1] при λy = 39 φу = 0,898. N2 / (cφyARy) = 2141,6 / (0,67 · 0,898 · 176,16 · 24) = 0,84 < 1. Устойчивость обеспечена. При проверке устойчивости из плоскости действия момента мы в запас устойчивости приняли площадь сечения с выключенной из работы частью стенки. Если проверка устойчивости по этой формуле не будет выполняться, вы можете уточнить расчет по п.7.16 [7].
Поскольку hw / tw = 97,65 / 0,8 = 122 > 2,2√Е / Ry = 67,4, то стенку колонны необходимо укрепить поперечными ребрами жесткости, расположенными на расстоянии (2,5...3) hw. Устанавливаем ребра на равных расстояниях с шагом 2630 мм (см. рис. 2.55). Размеры ребер: bh = hw / 30 + 40 = 976 / 30 + 40 = 72,5 мм. Принимаем bh = 75 мм; ts =2bh√Ry / E = 6 мм.
Расчет и конструирование подкрановой траверсы (см. рис.2.55). Высоту стенки траверсы принимаем равной 600 мм, что соответствует рекомендациям htr = (0,5...0,8) bn.
Толщину стенки определим из условия прочности на смятие: ttr = Dmax / (lef Rp γс) = 1657,63 / (42 · 36 · 1) = 1,1 см, где Dmax = 1657,63 кН - давление мостовых кранов; lef = bd + 2t = 36 + 23 = 42 см - длина сминаемой поверхности (bd = 36 см - ширина опорного ребра подкрановой балки; t = 3 см - толщина опорного листа подкрановой ступени); Rp = 36 кН/см2. Принимаем ttr = 12 мм.
Наружную полку соединим встык прямым швом, внутреннюю накладкой из листа 340 × 18 мм. Усилие во внутренней полке FB = N4 / 2 + M4 / (bB - tf) = 542,9 / 2 +
162
+ 116,7 / (0,489 - 0,0175) = 518,96 кН. Длина нахлестки накладки при kf = 6 мм (сварка ручная, электроды Э42): lH1 = FB / (2 f kf Rwf wf c) + 1 = 518,9 / (2 · 0,7 · 0,6 · 18,0 · 1 · 1) + 1,6 = 35,3 см.
Усилия в сечении 5 (5 - 9): N4 = -542,9 кН, М4 = 116,5 кН·м; N5 = -560,34 кН; М5 = -206,89 кН·м; lH2 = FB / (2 z kf Rwz wz c) + 1 = 518,96 / (2 · 0,6 · 16,65 · 1 · 1) + 1 = 27 см. Здесь Rwf = 18,0 кН/см2; Rwz = 0,45; Run = 0,45 · 37 = 16,65 кН/см2. Принимаем lH = 360 мм.
Усилие в наружной полке FH = N5 / 2 + М5 /(bВ - tf) = 560,34 / 2 + 206,89 (0,489 - 0,0175) = 719 кН. Напряжение в стыковом шве (сварка ручная, электроды Э42) FH / (tf lw Rwy) = 719 / [1,8(30 - 2(1,8)24] = 0,63 < 1.
Поскольку βz < βfRwf, расчет угловых швов проводим по металлу границы сплавления.
Вычисляем катеты угловых швов, соединяющих накладку со стенкой траверсы: kf = FB / (4βzlwRwzγwzγc) = 518,96 / (4 · l,05 · 59 · 16,65 · 1 · 1) = 0,13 cм. Принимаем kf = 6 мм.
Для сопряжения стенки траверсы с подкрановой ветвью: kf = Dmax / (4βzlwRwzγwzγc) = 1657,63 / (4 · 1,05 · 59 · 16,65 · 1 · 1) = 0,40 см (lw = 60 - 1 = 59 - расчетная длина шва). Принимаем kf = 6 мм.
163
