Конструктивные решения колонн подробно представлены в п.6.8[1].Подбор сечений колонн, проверку их прочности и устойчивости производят по общим правилам проектирования внецентренно сжатых элементов (см. 6.7[1]), ориентируясь на усилия, определенные при статическом расчете рамы. Но все это можно сделать, если известны расчетные длины колонн, которые непосредственно связаны с конструкцией каркаса здания. Рассмотрев этот вопрос, мы перейдем к конкретным примерам проектирования колонн постоянного сечения для бескрановых зданий, колонн с подкрановыми консолями для зданий с кранами небольшой грузоподъемности и ступенчатых колонн для зданий с мощными опорными мостовыми кранами.
Расчетную длину колонны в плоскости рамы можно определить путем расчета рамы на устойчивость. Это весьма трудоемкая задача, поэтому в практике проектирования используют приближенный подход, рассматривая колонну как изолированный стержень с идеализированными граничными условиями при загружении его постоянной по длине стержня нормальной силой и моментами, приложенными по концам.
Одним из главных факторов, влияющих на расчетную длину колонны, является возможность перемещения верхнего узла относительно нижнего при потере устойчивости. В этом смысле рамы делят на свободные и несвободные. Раму считают свободной, если все колонны находятся в одинаковых условиях, например все они загружены постоянной и снеговой нагрузками, и могут потерять устойчивость одновременно с перемещением верхних узлов относительно нижних. При таких условиях расчетную длину можно определить по рис. 6.11 [1], т.е. принять μ = 2, если колонна шарнирно соединена с ригелем или фундаментом, и μ = 1 - при жестком сопряжении с фундаментом и ригелем. Здесь мы не учли упругий поворот узла сопряжения ригеля с колонной, полагая жесткость ригеля бесконечно большой. При конечной жесткости ригеля коэффициент μ зависит от соотношения погонных жесткостей колонны и примыкающих к ней ригелей:
при жестком креплении колонны к ригелю и шарнирном к фундаменту
147
μ = 2√1+ 0,38 / n;(2.52)
при жестком креплении колонны и к ригелю и к фундаменту
μ = √(n + 0,56) / (п + 0,14).(2.53)
В формулах (2.52), (2.53)
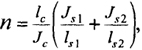(2.54)
где Jc, lc - соответственно момент инерции и длина проверяемой колонны; Js1 ,Js2, ls1, ls2 - соответственно моменты инерции и длины ригелей, примыкающих к этой колонне.
Если одна из колонн каркаса (расчетная колонна) нагружена в верхнем узле более остальных, то последние оказывают поддерживающее влияние, затрудняя перемещение верхнего узла расчетной колонны с помощью жесткого диска покрытия или продольных горизонтальных связей, т.е. проявляется эффект пространственной работы. При определении расчетной длины такой колонны обычно рассматривают совместную работу пяти рам. Коэффициенту μef для такой колонны определяют по формуле
μef = μ√Jc ∑ Ni / Nc ∑ Ji,(2.55)
где - коэффициент расчетной длины проверяемой колонны, вычисленный по формулам (2.52), (2.53); Jc ,Nc - соответственно момент инерции сечения и усилие в наиболее нагруженной колонне рассматриваемой рамы; ∑Ni и ∑Ji - соответственно сумма расчетных усилий и моментов инерции сечений всех колонн рассматриваемой рамы и четырех соседних рам (по две с каждой стороны); все усилия Ni, следует находить при той же комбинации нагрузок, которая вызывает усилие в проверяемой колонне.
Рекомендации по определению расчетных длин колонн для несвободных рам вы можете найти в нормах проектирования [7].
Для ступенчатых колонн расчетные длины верхней и нижней частей определяют раздельно, но исходя из условия одновременного достижения критического состояния при простом нагружении колонны (когда усилия в той и другой частях колонны изменяются пропорционально общему параметру нагружения). В этом случае отношение β между критическими силами для нижнего и верхнего участков колонны будет равно соотношению действующих в них усилий N2 и N1, которые приблизительно равны силам, приложенным в верхнем узле F2 и в уступе (F1 + F2).
148
Из условия [π2EJ1 / (μ1l)2] / [π2EJ2 / (μ2l)2] = β нетрудно найти отношение α1 между коэффициентами μ2 и μ1:
α1 =
=
√
s, β=
,(2.56)
и далее выразить коэффициент μ2 через коэффициент μ1:
μ2 = α1 μ1, но не более 3 (2.57)
Коэффициенты приведены в табл. П6.2, П6.3. Они получены из равенства Ncr = [π2EJ1 / (μ1l)2], где критические силы Ncr определены расчетом на устойчивость ступенчатых стоек.
При выполнении практических расчетов вы можете пользоваться данными табл. 2.15, обращаясь к таблицам приложения 6 лишь в случаях выхода характеристик расчетной колонны за пределы, указанные в табл. 2.15.
Таблица 2.15. Коэффициенты μ1 и μ2 для одноступенчатых колонн рам одноэтажных зданий при l2 / l1 ≤ 0,6 N2 / N1 ≥ 3
| Условия закрепления верхнего конца колонны |
μ1 для нижней части колонны |
μ2 для верхней части колонны |
| 0,3 > J2 / J1 ≥ 0,1 |
0,l > J2 / J1 ≥ 0,05 |
| Свободный |
2,5 |
3 |
3 |
| Закрепленный только от поворота |
2 |
2 |
3 |
| Неподвижный шарнирно опертый |
1,6 |
2 |
2,5 |
Аналогично определяют расчетные длины несвободных рам. Все необходимые данные для этого приведены в нормах проектирования [7].
Расчетную длину колонны или ее участка из плоскости рамы принимают равной расстоянию между точками закрепления колонны от смещений вдоль здания. Элементами закрепления могут служить подкрановые бачки, распорки и др. Здесь важно проследить за тем, чтобы эти элементы, в свою очередь, также были закреплены от смещений вертикальными связями между колоннами.
149
