2.2.3. Статический расчет рамы

При расчете рамы сквозной ригель заменяют эквивалентным по жесткости сплошностенчатым, момент инерции которого можно определить по формуле

EI_r = E (A_f1 z₁² + A_f2z₂²) ,(2.37)

где Af₁ и Af₂ - площади сечения нижнего и верхнего поясов фермы в середине пролета; z₁ и z₂ - расстояния от центра тяжести поясов до нейтральной оси фермы в сечении посередине пролета; μ - коэффициент, учитывающий уклон верхнего пояса и деформативность решетки фермы, принимаемый при уклоне верхнего пояса i = 1/8... 1/10 μ = 0,7; при i = 1:15 μ = 0,8; при i = 0 μ = 0,9.

Если площади сечений поясов неизвестны, то

EI_r = E

Mmaxhr

2Ry

  1,15μ,(2.38)

92

где М_mах - максимальный изгибающий момент в середине пролета ригеля как в простой балке от расчетной нагрузки (от собственного веса конструкций покрытия, включая нагрузку от подвесного оборудования, и снега); h_r - высота фермы в середине пролета; 1,15 - коэффициент, учитывающий отношение усредненной площади сечения поясов к площади нижнего пояса.

Осевая жесткость ригеля

EA_r ≈ 2EA_f =

4EIr

hr2

  ,(2.39)

где 2A_f - площадь сечения поясов ферм.

При расчете рам с колоннами ступенчато-переменного сечения изгибную и осевую жесткости подкрановой части колонны можно приближенно определить по формулам:

EI₁ =

E(R2 + 2Dmax) hn2

k2Ry

  ;(2.40) EA₁ =

4EI1

hn2

  ,(2.41)

где R₂ - опорная реакция ригеля от расчетной нагрузки (постоянной и снеговой); D_mах - расчетное давление на колонну от двух сближенных кранов. Для колонны среднего ряда D_max принимают от двух кранов большей грузоподъемности, сближенных в одном из смежных с колонной пролете; h_n - высота сечения нижнего участка колонны (расстояние от оси подкрановой ветви до наружной грани колонны крайнего ряда или расстояние между осями подкрановых ветвей для колонн средних рядов); k₂ - коэффициент, зависящий от шага колонн и их высоты - k₂ = 3,2. ..3,8 при шаге рам 12 м, k₂ = 2,5...3,0 при шаге рам 6 м. Меньшие значения k₂ следует принимать при кранах с малой грузоподъемностью и при большой высоте колонн.

По этим же формулам можно определять жесткости колонн постоянного сечения (см. рис. 2.8), принимая k₂ = 2,2.. .2,5.

Жесткости верхних (надкрановых) частей ступенчатых колонн

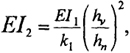(2.42) EA₂ =

4EI2

hv2

  ,(2.43)

93

где h_v - ширина сечения верхнего участка колонны; k₁ - коэффициент, учитывающий фактическое неравенство площадей и радиусов инерции поперечных сечений верхней и нижней частей колонны. При шарнирном сопряжении ригелей с колоннами k₁ =1,8...2,0 для колонн крайних рядов, k₁ = 2,0...2,3 для колонн средних рядов. При жестком сопряжении ригелей с колоннами k₁ = 1,2...1,8. Меньшие значения принимают для кранов небольшой грузоподъемности.

Жесткости условных горизонтальных стержней, объединяющих верхние и нижние участки колонн, задают на два-три порядка больше жесткостей нижних участков колонн.

Жесткости колонн зданий бескрановых и с подвесным крановым оборудованием, а также зданий с мостовыми кранами, опираемыми на подкрановые стойки, на этапе формирования исходных данных можно подобрать, исходя из заданной при компоновке рамы высоты сечения колонны, ориентируясь, например, на прокатные профили. Пользуясь сортаментом, выбирают по заданной высоте сечения колонны профиль и устанавливают тем самым площадь и момент инерции сечения.

Для статического расчета рамы без использования ЭВМ достаточно знать только соотношения моментов инерции элементов рамы. Эти соотношения можно принимать в пределах

J_n/J_v = 5...10; J_r/J_n = 2...6.

В многопролетных зданиях отношения моментов инерции нижнего участка средней колонны J_ns и верхнего ее участка J_vs к моментам инерции сечений соответствующих участков крайних колонн обычно составляют:

J_ns / J_v = 10...30 при одинаковом шаге внутренних и наружных колонн; 20...60 - при шаге внутренних колонн вдвое большем, чем наружных;

J_vs / J_v = 1,5...3 при одинаковом шаге внутренних и наружных колонн; 2,5...7 - при шаге внутренних колонн вдвое большем, чем наружных.

Дальнейший расчет вы можете выполнять, опираясь на известные методы строительной механики. При использовании метода перемещений опорные реакции стоек переменного сечения от единичных перемещений и от внешних нагрузок вы можете определять по формулам, приведенным в табл. П5.2...П5.4.

При расчете рамы на нагрузки, приложенные к колоннам, если выполняется условие k ≥ 6/(1 + 1,1√μ), где k = J_rH/J_nl; μ = (J_n/Jv) - 1, можно принимать

94

жесткость ригеля бесконечно большой. Это дает возможность понизить степень кинематической неопределимости рамы при ее расчете методом перемещений, принимая углы поворота сечений в местах сопряжения ригелей с колоннами, равными нулю. Так, при расчете многопролетной рамы с одинаковой высотой пролетов достаточно наложить только одну связь, препятствующую линейному перемещению в уровне ригеля, и, следовательно, свести расчет к решению задачи с одним неизвестным. Все это позволяет приближенно оценить напряженно-деформированное состояние каркаса на отдельные виды загружений, используя лишь микрокалькулятор. Однако, учитывая необходимость выполнения раздельных расчетов по многим видам загружений, вычислительные процедуры очень трудоемки. С этих позиций целесообразно выполнять статические расчеты на ЭВМ по разработанным для этих целей программным комплексам (Лира, Парус, Космос, Астра, Экспресс, Рама и др.) В большинстве из них реализован алгоритм метода перемещений с учетом, наряду с изгибными, еще и продольных деформаций стержней. Такая модель дает существенные уточнения для схем с сосредоточенными узловыми нагрузками, направленными вдоль стержней с малой осевой жесткостью.

Роль проектировщика при выполнении статических расчетов на ЭВМ несколько снижается. Центр тяжести в решении смещается на оценку расчетной схемы и правильное выполнение формальных процедур по составлению исходной информации. Все вычисления возлагаются на ЭВМ с полным доверием к результатам. Однако, ввиду возможных ошибок и неточностей в задании исходной информации, расшифровке данных и др., выданные результаты могут быть ошибочными. Указанные обстоятельства требуют повышенного внимания на анализ решений, их соответствия расчетной схеме по нагрузкам и условиям закрепления, по характеру эпюр, по условиям равновесия всей системы в целом и выделенных из системы отдельных частей.

Все, что мы с вами обсудили, касалось расчета плоских рам. На самом деле поперечные рамы каркаса связаны диском покрытия, продольными связями по нижним поясам ферм, другими элементами (например, тормозными конструкциями в крановых зданиях) и не являются свободными.

При нагружении всех рам, например при действии ветровых нагрузок, горизонтальные перемещения рам одинаковы и их совместная работа не проявляется. Если же нагрузка приложена к отдельным рамам, например крановая, соседние менее нагруженные рамы за счет имеющихся связей также включаются в работу и сдерживают перемещения рассматриваемой рамы, т.е. возникает эффект пространственной работы каркаса.

95

Учет этого фактора позволяет снизить моменты в нижних сечениях колонн и уменьшить горизонтальные перемещения каркаса.

Если расчет выполняется на ЭВМ при использовании программ, построенных на методе конечного элемента, вы можете рассмотреть каркас как единую пространственную стержневую систему и, введя жесткостные характеристики связей, получить результаты расчета с учетом пространственной работы. При этом достаточно рассмотреть блок из 5...7 рам.

При расчете рамы методом перемещений вручную или с использованием программ, построенных на основе этого метода, учет пространственной работы каркаса может быть выполнен путем введения коэффициента пространственной работы α_pr. Он показывает, насколько перемещение рамы, работающей в пространственном блоке Δ_pr, меньше перемещения плоской рамы Δ_рl, т.е. α_pr = Δ_pr / Δ_pl. Этот коэффициент зависит от жесткости диска покрытия, колонн, связей, шага рам, высоты здания и других параметров и определяется по методике, изложенной в [2].

96