|
|
 |
 |
 |
 |
Проверочные расчеты конструкций выполняют с учетом выявленных дефектов и повреждений, уточненных нагрузок, расчетных схем и прочности материала.
Для элементов конструкций, имеющих коррозионный износ, за расчетное принимают сечение, полученное по результатам обмеров конструкции в местах, очищенных от продуктов коррозии.
Проверку прочности элементов, имеющих вырезы, производят по площади нетто с учетом эксцентриситета от смещения центра тяжести ослабленного сечения относительно центра тяжести неповрежденного сечения.
При проектировании стержней решетки стропильных ферм с гибкостью λ > 60 возможность их случайных искривлений учитывают коэффициентом условий работы γс = 0,8. При проверочных расчетах эксплуатируемых стропильных ферм этот коэффициент может быть принят равным 1, а стержни рассчитаны с учетом фактических искривлений, выявленных
436
при обследовании. Такой же расчет проводят для всех сжатых элементов конструкций, имеющих искривления.
Сжатые сплошностенчатые элементы металлических конструкций, имеющие искривления, рассчитывают как внецентренно сжатые. Отличие работы искривленного стержня от внецентренно сжатого (рис. 9.3) рекомендуется учитывать умножением стрелки искривления в ненагруженном состоянии стержня f0 на поправочный коэффициент k перехода от стрелки искривления к эквивалентному эксцентриситету e.
Рис. 9.3. К расчету искривленных сжатых стержней:а - состояние при измерении стрелки искривления f под нагрузкой; б - ненагруженное состояние, характеризуемое стрелкой f0; в - расчетная схема стержня с эксцентриситетом e.
Стрелка искривления стержня в ненагруженном состоянии f0 меньше стрелки искривления f, замеренной при обследовании конструкций, находящихся под нагрузкой. Ее значение определяют по формуле:
f0 = ψf,
(9.3)
где ψ - поправочный коэффициент, вычисляемый по формуле:
ψ = 1 - 0,1
,
(9.4)
σ = N/A - напряжение в стержне во время замера стрелки /
Если усилие в стержне N в момент замера стрелки определить невозможно, несколько в запас, коэффициент ψ можно принять равным 1.
Эквивалентный эксцентриситет е принимают равным произведению е0 = kf0. Поправочный коэффициент k вычисляют по формуле:
k = 0,82 + 0,1
.
(9.5)
В результате проверочный расчет искривленных стержней выполняют по формуле (6.85) [1].
Часто при обследовании стальных ферм обнаруживают сжатые стержни, имеющие искривления в двух плоскостях. Проверку устойчивости таких стержней следует выполнять по формуле:
437
σ =
≤ Ryγc,
(9.6)
где φuv - коэффициент снижения несущей способности сжатого стержня, имеющего искривления в двух плоскостях, определяемый по табл. 9.4, 9.5 в зависимости от условной гибкости в плоскости симметрии сечения λx =
√
, и условных относительных стрелок искривления в двух плоскостях:
U0 =
√E |
| Ry; V0 =
,
где lx и lу - расчетные длины стержней; fx0 и fyo - стрелки искривления, определяемые по формуле (9.3).
Стержни, имеющие искривления только из плоскости фермы, рассчитывают аналогично, принимая U0 = 0.
Разработана методика учета вырезов и вмятин в полках уголков при проверке их устойчивости [8].
Проверочные расчеты соединений металлических конструкций проводят по тем же формулам, что и при проектировании, с учетом фактических размеров (сварных швов, болтов, заклепок) и расчетных сопротивлений, определенных в соответствии с п. 9.1.4.
Пример 9.2. Проверить устойчивость сжатого раскоса стропильной фермы, искривленного в плоскости фермы f = 18 мм (рис.9.4). Расчетное сопротивление Ry = 21 кН/см2. Сечение раскоса из двух уголков 90×8. Длина раскоса l = 400 см. Усилие в раскосе во время измерения стрелки искривления (отсутствовала снеговая нагрузка) N1 = 180 кН. Расчетная нагрузка N = 280 кН.
Предварительно определяем необходимые геометрические характеристики сечения стержня: А = 27,8 см2; Jx = 212 см2; ix = 2,76 см; Z0 = 2,51 см; lх = 0,8 · 400 = 320 см;
Wx =
=
= 32,6 см3; λx =
√
=
√
= 3,7.
Определяем поправочный коэффициент ψ по формуле (9.4):
ψ = 1 - 0,1
= 1 - 0,1
= 0,58,
где σ = N1/A = 180/27,8 = 6,5 кН/см2.
По формуле (9.3) f0 = ψf = 0,58 · 1,8 = 1 см. Поправочный коэффициент k для перехода от стрелки f0 к эксцентриситету е вычисляем по формуле (9.5). Предварительно определяем mf0 =
=
= 0,85. По табл.П8 [1] при Af/ Aw = 1 и 0,1 ≤ m ≤ 5
η = (1,5 - 0,1m) - 0,02(5 - m)λ = (1,5 - 0,1 · 0,85) - 0,02·(5 - 0,85)3,7 = 1,108;
438
Таблица 9.4. Коэффициенты φuv для стержней из равнополочных уголков, шарнирно закрепленных в двух главных плоскостях ( μх = 1, μy =1)
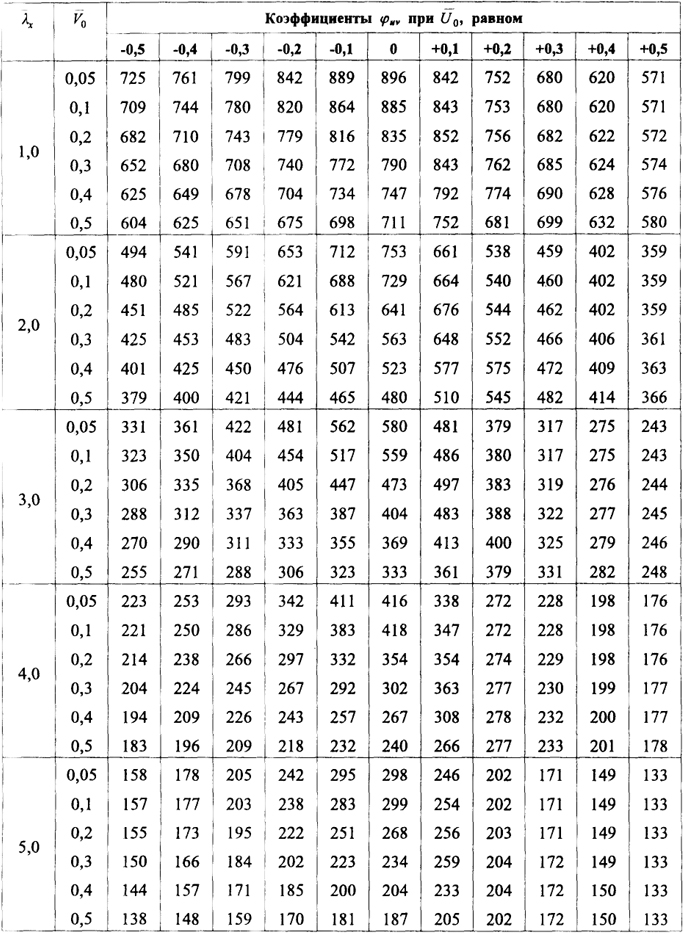
Примечания. 1. Значения коэффициента φuv в таблице увеличены в 1000 раз.
2. Значение V0 принимается со знаком "+" при эксцентриситете в сторону полок.
439
Таблица 9.5. Коэффициенты φuv для стержней из равнополочных уголков, упругозащемленных в плоскости симметрии и шарнирно закрепленных из этой плоскости (μх = 0,8, μy = 1)
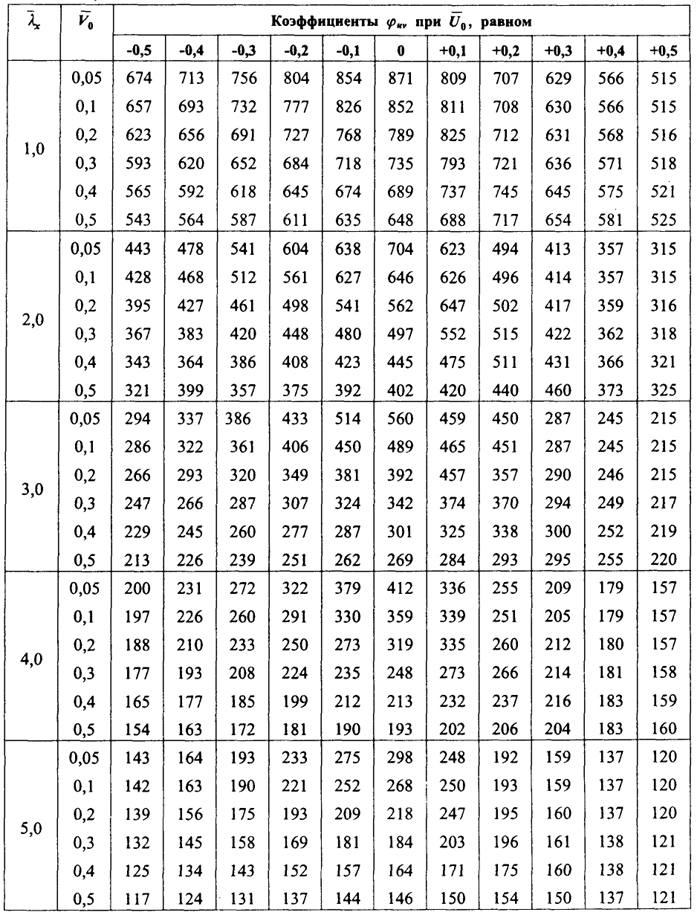
Примечания: 1. Значения коэффициента φuv в таблице увеличены в 1000 раз.
2. Значение U0 принимается со знаком "+" при эксцентриситете в сторону полок.
440
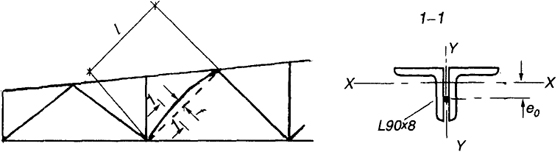Рис. 9.4. К примеру 9.2
k = 0,82 + 0,1
= 0,82 + 0,1
= 0,85;
e0 = kf0 = 0,85 · 1 = 0,85 см; mcf = η
= 1,108
= 0,8.
По табл. П7.1 [1] при mef = 0,8 и λ = 3,7 определяем φe = 0,382. Проверяем устойчивость раскоса на действие расчетного усилия N = 280 кН:
σ =
=
= 26,4 кН/см2 > Ry = 21 кН/см2.
Устойчивость раскоса при действии расчетного усилия не обеспечена. При отсутствии снега σ =
= 16,9 кН/см 2 < Rу; устойчивость обеспечена.
Пример 9.3. Проверить устойчивость сжатого раскоса стропильной фермы, искривленного в двух плоскостях (рис. 9.5). Искривление в плоскости фермы (относительно оси x-x) fx = 15 мм; искривление из плоскости фермы (относительно ocи y-y) fy = 20 мм. Расчетное сопротивление Ry = 21 кН/см2. Сечение раскоса из двух уголков 90×6. Длина раскоса l = 450 см. Усилие в раскосе во время измерения стрелок искривления N1 =70 кН. Расчетное усилие 120 кН.
Предварительно определяем необходимые геометрические характеристики стержня: А = 21,2 см2; ix =2,78 см; iy = 4,04 см;
λx =
=
√
= 4,13; λy =
√
=
√
= 3,56.
Напряжение в стержне при замере стрелки искривления составило σ = N1/A = 70/21,2 = 33 кН/см2. Определяем поправочный коэффициент по формуле
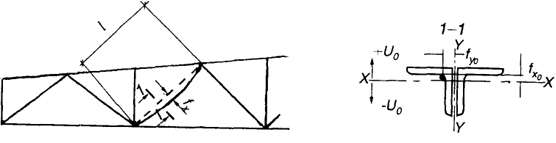Рис. 9.5. К примеру 9.3
441
ψx = 1 - 0,1
= 1 - 0,1
= 0,73, ψy = 1 - 0,1
= 0,8.
По формуле (9.3) f0x = ψxfx = 0,73 · 1,5 = 1,1 см; f0y = 0,8 · 2 = 1,6 см. Условные относительные искривления:
U0 =
√
=
√
= 0,1; V0 =
√
= 0,11.
По табл. 9.5 определяем φuv при λx = 4,13, U0 = +0,1, V0 = 0,11; φuv = 0,327. Производим проверку устойчивости стержня по формуле (9.6):
σ =
=17,3 кН/см2 < Ry = 21 кН/см2.
Устойчивость стержня (с учетом искривлений) обеспечена.
442
|
 |
 |
 |
 |
|
