Провисающие мембраны используют в покрытиях круглых и эллиптических в плане зданий. Поверхность покрытия может быть выполнена в форме параболоида вращения, сферы, эллиптического параболоида и даже конуса, хотя в последнем случае имеет место уже иной класс оболочек с нулевой гауссовой кривизной и, следовательно, с одноосным напряженным состоянием. Внешне все они похожи друг на друга, а в работе имеют некоторые различия. Тем не менее трудно выделить какую-то форму, наиболее рациональную по всем показателям. В каждом конкретном случае объективным критерием может быть только вариантное проектирование.
Как и цилиндрические мембраны, все перечисленные типы оболочек для уменьшения деформативности требуют стабилизации. Кроме указанных для цилиндрических оболочек способов, в оболочках на круглом плане широко практикуют использование технологических нагрузок. Так, в покрытии цеха металлоконструкций в Австрии коническая мембрана стабилизирована весом мостовых кранов, одна из опор которых передает свои усилия в центр мембраны. На рис. 8.48, а показана сферическая мембрана покрытия универсального спортивного зала в С.-Петербурге
414
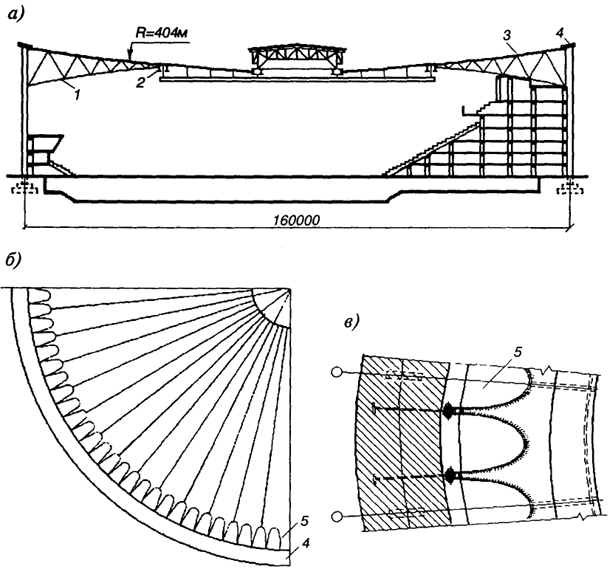Рис. 8.48. Мембранное покрытие спортивного зала:1 - стабилизирующая форма;
2 - промежуточное кольцо;
3 - мембрана;
4 - опорное кольцо;
5 - вырезы в мембране
из стального листа толщиной 6 мм, стабилизированная в середине покрытия тяжелой железобетонной плитой с размещением на ней технологического оборудования. Дополнительно мембрана стабилизирована 56 радиальными тросовыми фермами с верхними поясами из швеллера, который одновременно служит направляющим элементом монтажной постели. Нижний пояс фермы прикреплен к кольцу диаметром 72 м, свободно подвешенному к мембране и устроенному для того, чтобы не передавать сосредоточенных усилий в поясах ферм на мембрану. При проектировании этого покрытия были предусмотрены эллиптические вырезы (рис. 8.48, б, в), для устранения влияния местных напряжений краевого эффекта и обеспечения свободы кольцевых деформаций мембраны. Практика возведения подобных покрытий показала, что влияние краевого эффекта не столь значительно, поэтому от вырезов в околоконтурной зоне можно отказаться.
415
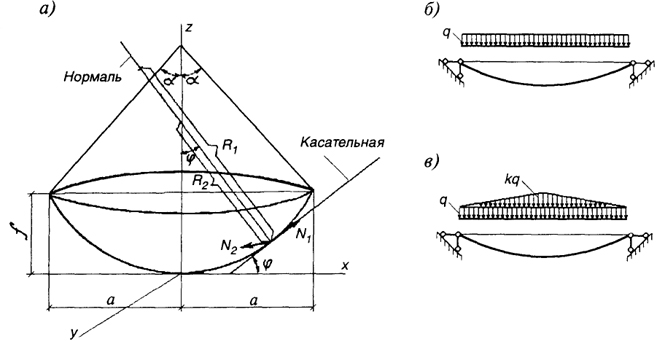Рис. 8.49. Параболоид вращения:а - расчетная схема;
б - загружение постоянной нагрузкой;
в - то же, снеговой
Для круглых в плане зданий при равномерно распределенной по покрытию нагрузке равновесной формой будет параболоид
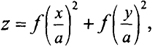(8.90)
где а - радиус покрытия; f - стрела провеса мембраны. Такая форма поверхности обеспечивает равномерное распределение меридиональных и кольцевых усилий по поверхности мембраны, что позволяет делать ее всю одинаковой толщины.
Для проверки прочности мембраны по формулам (8.88) нужно найти усилия с помощью уравнения Лапласа (8.87), а для этого надо предварительно вычислить радиусы кривизны и некоторые другие геометрические характеристики поверхности мембраны, к определению которых мы и перейдем.
Сечение поверхности (рис. 8.49, а), описываемой уравнением (8.90), вертикальными плоскостями, проходящими через ось 0z, дает параболы z = f(x/a)2 с радиусами кривизны в вертикальной плоскости, равными:
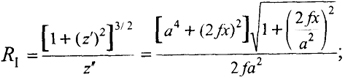(8.91)
416
Нормальная к поверхности мембраны составляющая внешней нагрузки
р = qcos φ.
(8.92)
Функции угла φ, входящие в равенства (8.91), (8.92), можно определить по известным формулам:
sin φ =
; cos φ =
; tg φ = z' =
x.
(8.93)
Вначале определим усилия в мембране от равномерно распределенной нагрузки (рис. 8.49, б). Меридиональное усилие найдем из условия равновесия отсеченной горизонтальной плоскостью части мембраны: 2πх N1 sin φ = G = πx2q, откуда
N1 = qx / (2 sin φ).
(8.94)
Подставляя это значение в уравнение (8.87), определим кольцевое усилие
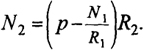(8.95)
Поступая аналогичным образом, можно найти усилия в мембране от снеговой нагрузки (рис. 8.49, в), нормальная к поверхности составляющая которой распределена по закону
(8.96)
Будем иметь
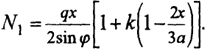(8.97)
Формула для определения кольцевого усилия (8.95) не меняется, но в нее должны быть подставлены значения р и N1, вычисленные по формулам (8.96), (8.97).
Перемещение оболочки по нормали w [3] от действия равномерно распределенной нагрузки по рис. 8.49, б
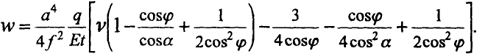(8.98)
Стрелка перемещения в середине оболочки при φ = 0 будет равна
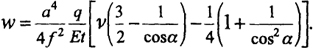(8.99)
Пример 8.6. Рассчитать мембранное покрытие диаметром 200 м в форме квадратичного параболоида. Район строительства - Москва. Материал покрытия - сталь С235. Стрела провеса мембраны 12 м.
417
Таблица 8.6. Нагрузки на 1 м2 покрытия (к примеру 8.6)
| Состав покрытия |
Нормативная нагрузка, кН/м2 |
Коэффициент надежности по нагрузке |
Расчетная нагрузка, кН/м2 |
| Постоянная нагрузка |
| Гидроизоляция (трехслойный рулонный ковер) |
0,1 |
1,3 |
0,13 |
| Цементная стяжка 2 см, плотностью 1800 кг/м3 |
0,36 |
1,3 |
0,468 |
| Теплоизоляция (пенобетон толщиной 12 см, плотностью 600 кг/м3) |
0,60 |
1,2 |
0,72 |
| Стальная мембрана толщиной 6 мм (плотность стали 7850 кг/м3) |
0,471 |
1,1 |
0,518 |
| Итого |
1,531 |
- |
1,836 |
| Временная нагрузка |
| Снеговая нагрузка для III района |
1,0 |
1,4 |
1,4 |
| Итого |
2,531 |
|
3,236 |
Нагрузки на покрытие приведены в табл.8.6.
Определим усилия в средней части мембраны на окружности радиусом 15 м.
Предварительно находим геометрические характеристики мембраны по формулам
tg φ =
15 = 0,036; sin φ =
; cos φ =
= 1;
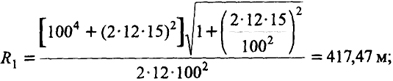
R2 = 15 / 0,036 = 416,67 м.
В примере рассмотрим расчет покрытия только при первом варианте его загружения снеговой нагрузкой (см. рис. 8.49, б), т.е. принимая ее равномерно распределенной по всему покрытию. Тогда полная (постоянная и временная) расчетная нагрузка будет равна 3,236 кН/м2. Нормальную к поверхности мембраны составляющую внешней нагрузки определим по формуле (8.92) р ≈ q = 3,236 кН/м2.
Меридиональное и кольцевое усилия найдем по формулам (8.94), (8.95):
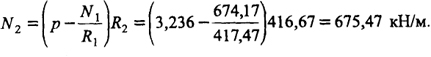
В данном примере можно было сразу найти усилия N1, N2, обратив внимание на приблизительное равенство радиусов кривизны в меридиональном и кольцевом направлениях
418
R1 ≈ R2 = Rmах = 417,47 м. Тогда в соответствии с уравнением Лапласа N1 ≈ N2 = pRmax / 2 = 3,236 · 417,47 / 2 = 675,47 кН/м.
Определим усилия в районе кольца мембраны, для чего повторим все вычисления при x = 100 м. Будем иметь:
tg φ = 0,24; sin φ = 0,2334; cos φ = 0,9724; р = 3,15 кН/м2;
R1 = 453,18 м; R2 = 428,45 м; N1 = 674,81 кН/м; N2 = 711,63 кН/м.
Найдем толщину мембраны по наибольшему усилию N2 = 711,63 кН/м; t ≥ N2 / (Ryγc) = 711,637 (23 · 0,8 · 100) = 0,387 см. Назначаем толщину мембраны 4 мм.
Проверим прочность мембраны по приведенным напряжениям:
σ1 = N1 / t = 674,81 / (0,4 · 100) = 16,87 кН/см2; σ2 = 711,63 / (0,4 · 100) = 17,79 кН/см2;
√16,872 - 16,87 · 17,79 + 17,792 = 17,35 кН/см2 < 23 · 0,8 = 18,4 кН/см2.
Определим по формуле (8.99) перемещение оболочки в середине пролета от нормативной снеговой нагрузки
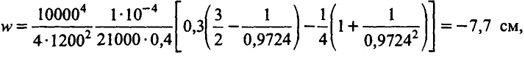
что значительно меньше величины //200.
Столь малая величина перемещения оболочки объясняется тем, что оно вызвано снеговой нагрузкой с таким же законом распределения ее по покрытию как и постоянная нагрузка, поэтому обусловлено лишь упругими деформациями без кинематических перемещений. Перемещение оболочки от нагрузки, расположенной на части покрытия, может быть существенно большим, поэтому на стадии рабочего проектирования следует оценить деформативность покрытия при всех возможных видах загружения его снеговой нагрузкой, что можно сделать на основе численных расчетов.
419
