Рассмотрим примеры определения сейсмических сил, возникающих при колебаниях линейного осциллятора с различными заданными законами движения основания. Помимо методического эти примеры имеют и познавательное значение, поскольку позволяют схематически проследить путь развития теории сейсмостойкости.
1. Пусть движение основания следует гармоническому закону
Δ(t) = Δ0 sin θ t,(2.15)
Пренебрегая пока эффектом диссипации энергии, уравнение движения линейного осциллятора запишем в виде:
z..+ω2z = W0 sin θ t,(2.16)
где W0 = Δ0θ2- амплитудное значение ускорения основания.
Решение уравнения (2.16) при нулевых начальных условиях имеет вид:
(2.17)
где
- коэффициент динамичности.
Вычисляя по формуле (2.5) сейсмическую силу, имеем с учетом (2.17):
S = -m(Δ.. + z..) = m W0 β sin θ t.
(2.18)
Из (2.18) следует
тaxS = ксβQ,(2.19)
где по-прежнему кс = W0 / g- сейсмический коэффициент.
Нетрудно видеть, что выражение в точности совпадает с формулой Мононобе (2.2).
Учет сил сопротивления приводит к корректировке выражения для коэффициента динамичности:
(2.20)
29
Исследование графиков динамического коэффициента при различных значениях параметра γ, называемых амплитудно-частотными характеристиками системы, содержится в общем курсе динамики сооружений. Напомним только, что учет сил сопротивления приводит к резкому снижению значения этого коэффициента в резонансной зоне 0,6 ≤ θ/ω ≤ 1,3; причем при θ = ω имеем β = 1/γ.
Хотя, как об этом уже говорилось, теория Мононобе и не нашла большого практического применения, тем не менее в развитии теории сейсмостойкости она сыграла очень большую роль. Впервые было обращено внимание на свойство системы сильнее реагировать на ту компоненту колебательного процесса основания, частота которой наиболее близка к ее собственной частоте. Кстати говоря, основанная на этом идея "вывода" системы из резонансной зоны, конечно, соответствующим образом видоизмененная, находит широкое применение в современных методах сейсмозащиты зданий и сооружений.
Существенным недостатком теории Мононобе является то, что она не учитывает начальных условий, т.е. не предусматривает существования переходного режима, когда на процесс вынужденных колебаний накладывается процесс затухающих свободных колебаний.
2. Учет переходного режима легко достигается, если вместо синусоидального закона движения основания принять косинусоидальный закон, что в свое время и было предложено в работах К.С. Завриева, а затем - А.Г. Назарова.
Принимая
Δ(t) = Δ0cosθt,
нетрудно построить решение уравнения движения (2.9) в следующем виде
| z(t)= |
W0 |
β(cosθt – sinωt) |
| ω2 |
(2.21)
Поскольку наибольшее значение выражения в скобках равно ± 2, то и значение динамического коэффициента в данном случае получается вдвое бóльшим.
Вообще говоря, в динамике сооружений этот эффект характерен для случая внезапного приложения нагрузки, что качественно согласуется с рассматриваемым здесь случаем, когда при t = 0 Δ =Δ 0.
Данная аналогия впоследствии нашла свое развитие в работах А.Г. Назарова, предложившего рассматривать процесс сейсмического воздействия в виде одного или совокупности нескольких кратковременных импульсов ускорения, названного им "сейсмическим ударом".
30
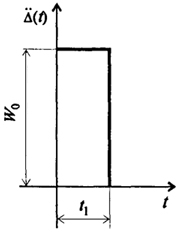
Рис. 2.6. Воздействие в виде прямоугольного импульса ускорения
3. Рассмотрим случай кратковременного действия ускорения по закону прямоугольника (рис. 2.6).
Здесь W0 - максимальное ускорение основания.
При нулевых начальных условиях для консервативной системы решение данной задачи можно представить в виде интеграла Дюамеля
| z(t)= |
- |
W0 |
t1∫0 |
sinω(t - τ)dτ |
| ω |
(2.22)
после несложных преобразовании из (2.22) находим
| z(t) = |
-2 |
W0 |
sin |
ωt1 |
sin ω ( t- |
t1 |
) |
| ω2 |
2 |
2 |
(2.23)
Пусть время действия ускорения t1 < Т/2, где Т - период собственных колебаний линейного осциллятора, но, вместе с тем больше времени, необходимого для распространения волны деформации от основания до сосредоточенной массы.
Считая t1 малым, из (2.23) имеем
(2.24)
Разумеется, это решение будет справедливым при условии t>>t1. По аналогии с импульсом силы величина W0 t1 =JW называется импульсом ускорения. С учетом этого из (2.24) имеем
(2.25)
Эту формулу уместно сопоставить формуле для определения максимального смещения при действии мгновенного импульса силы J:
Вследствие этого вводится понятие мгновенного импульса ускорений. Под этим определением следует понимать ускорение, действующее в продолжении бесконечно малого промежутка времени, но имеющее столь большую величину, что его импульс JW является конечной величиной [10].
Вычисляя сейсмическую силу для случая кратковременного импульса, имеем
| S(t)= Q |
W0 |
(1+ |
2πt1 |
) sin ω t |
| g |
T |
31
Этому выражению можно придать вид (2.19), где
При введении концепции мгновенного импульса t1→0, β→0 формула для определения максимального значения сейсмической силы обращается в формулу статической теории S = KCQ, с тем лишь парадоксальным результатом, что при этом сейсмический коэффициент может иметь сколь угодно большое значение.
4. Спектральная теория сейсмостойкости основана на введении понятия спектра ускорений (а также смещений и скоростей смещений). Этот метод расчета лежит в основе строительных норм СНиП II-7-81.
Для неконсервативного линейного осциллятора решение дифференциального уравнения движения при нулевых граничных условиях записывается в виде (2.14) (при ω 1 = ω)
| z(t) = - |
1 |
t∫0 |
Δ..(τ) e
sin ω (t - τ)dτ |
| ω |
2.27
Значение сейсмической силы, вычисленное по формуле (2.5), может быть представлено в следующем виде:
S(t)= -m[Δ..(t)+z..(t)]=rz(t)(2.28)
где
Используя это представление и подставляя это и (2.27) в (2.28), получаем
| S(t) = - |
2π |
m |
t∫0 |
Δ.. (τ) e
sin ω (t - τ)dt |
| T |
(2.29)
Запишем это выражение в виде
(2.30)
где
| W(t,γ,T) = |
2π |
t∫0 |
Δ..(τ) e
sin ω(t - τ) dτ |
| T |
(2.31)
Отсюда имеем
| m ax S = |
Q |
m axt| W (t, γ, T) | = |
Q |
CW(T) |
| g |
g |
(2.32)
32
Функция СW(T), представляющая собой максимальное значение функции W(t,γ,T) на рассматриваемом отрезке времени, является функцией параметров γ и T. При фиксированном значении γ и при заданной функции Δ..(t) зависимость между СW(T) и Т можно выразить некоторой кривой, называемой спектральной кривойускорений, а сама функция СW(T) носит название спектра ускорений.
Аналогичным образом могут быть введены спектры скоростей СV(T) и спектры смещений СZ(T), между которыми имеют место очевидные зависимости
| Cw(T)= |
2π |
Cv(T)=( |
2π |
)2Cz(T) |
| T |
T |
(2.33)
Задавая различные законы изменения входного воздействия Δ..(t), соответствующие тем или иным реальным землетрясениям, можно получить семейство спектральных кривых, отличающихся друг от друга. Это естественным образом объясняется различием как физических параметров землетрясений (магнитуда, эпицентральное расстояние, грунтовые условия и т.д.), так и физическими свойствами самого осциллятора.
Вместе с тем оказывается, что все спектральные кривые обладают некоторыми общими свойствами. Например, на спектрах ускорений при периодах свободных колебаний от 0,2 до 0,6 сек. наблюдаются пики, которые с ростом периода собственных колебаний осциллятора сглаживаются. Заметим, что при Т < 0,2 достоверность получаемых данных резко снижается в силу разрешающей способности самих приборов, записывающих акселерограммы. Поэтому было сочтено целесообразным на этом участке оставлять пиковые значения спектральных кривых.
Если теперь при достаточном представительстве исходной информации провести огибающую всех полученных спектральных кривых, то эту кривую можно принять в качестве расчетной кривой, определяющей возможные максимальные значения инерционных сил линейного осциллятора, вычисляемые согласно формуле (2.32).
33
