Одномассовая система (рис. 2.5, а) при условии, что невесомый стержень, поддерживающий массу, является линейно деформируемым, носит название линейного осциллятора. При этом колебательный процесс может рассматриваться как в виде незатухающих колебаний (консервативная система), так и в виде затухающих колебаний (неконсервативная система).
25
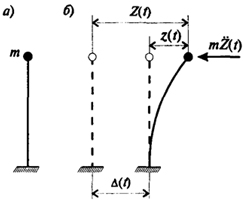
Рис. 2.5. Расчетная схема линейного осциллятора
Рассмотрение колебательного процесса имеет фундаментальное значение как в динамике сооружений, в общем, так и в сейсмике, в частности, поскольку позволяет выявить основные закономерности протекания этого процесса, так или иначе проявляющиеся в случае более сложных расчетных схем.
Рассмотрим основные подходы к постановке задачи расчета линейного осциллятора на сейсмические воздействия в том линейного осциллятора простейшем случае, когда это воздействие
моделируется горизонтальным перемещением основания, происходящим по заданному закону Δ = Δ( t), а система имеет одну степень свободы, определяемую горизонтальным перемещением сосредоточенной массы (рис. 2.5, б).
Полное перемещение массы т в любой момент времени Z(t) складывается из переносного перемещения Δ (t) и относительного перемещения z(t), вызванного изгибом стержня (рис. 2.5, б):
Z(T)=Δ(t)+z(t)(2.4)
Как известно, в динамике сооружений существуют два основных метода составления уравнений движения - метод сил и метод перемещений.
Используя метод сил, в основу составления уравнения движения положим равенство (2.4). Вводя в рассмотрение перемещение б массы в горизонтальном направлении, вызванное действием единичной силы и учитывая, что инерционная сила, возникающая при колебаниях, может быть представлена в виде:
S = -mz..(t)(2.5)
(здесь, как обычно, точками обозначены производные по времени), из 2.4 получаем:
z(t) = Δ(t) - δmz..(t).(2.6)
Отсюда следует:
δm z..(t)+z(t) = Δ(t).(2.7)
Если вспомнить, что для консервативной системы с одной степенью свободы δm = 1/ω2, где ω - частота собственных (в данном случае - свободных) колебаний, то уравнение (2.7) легко представить в виде:
z..(t) + ω2z(t) = ω2Δ(t).(2.8)
Уравнение (2.8) является уравнением движения системы, записанным относительно полного перемещения массы. С помощью (2.4) это уравнение
26
можно представить в виде, когда искомой функцией будет являться относительное перемещение z(t):
z.. (t) + ω2z(t) = - Δ..(t)(2.9)
Теперь составим уравнение движения, применяя метод перемещений. Схема остается прежней (рис. 2.5), только к инерционной силе следует добавить восстанавливающую силу (силу упругости), равную rz(t), где r= 1/δ представляет собой жесткость линейного осциллятора. Составляя уравнение равновесия массы, с учетом (2.4) имеем
m[Δ.. (t) + z..(t)] + rz(t) = 0
Подставляя сюда r/m = 1/mδ = ω2, получаем уравнение
z..(t)+ (ω2z(t) = - Δ..(t),
полностью совпадающее с уравнением (2.9).
Здесь следует обратить внимание на то обстоятельство, что в качестве внешнего воздействия могут быть использованы известные функции изменений во времени либо перемещений, что свойственно постановкам динамических задач при возбуждении кинематического типа [18], либо ускорений, что характерно для постановки задач сейсмостойкости сооружений.
В случае учета диссипации энергии при составлении уравнений движения должны дополнительно учитываться силы сопротивления.
Опуская подробности, известные из курса динамики сооружений, отметим, что в практике сейсмических расчетов неконсервативных систем в настоящее время наиболее часто применяются две модели учета сил сопротивления - по гипотезе Фойгта и по гипотезе Е.С. Сорокина.
Напомним, что по гипотезе вязкого сопротивления Фойгта силы сопротивления пропорциональны скорости перемещений Ф = βz.(t), где β - коэффициент пропорциональности, определяемый, вообще говоря, путем экспериментальных исследований. В этом случае дифференциальное уравнение движения линейного осциллятора записывается в виде:
z..(t)+2α z. (t) + ω2z(t) = - Δ.. (t),(2.10)
где 2α = β / m.
Согласно гипотезе неупругого сопротивления Е.С. Сорокина, применяемой для расчета строительных конструкций, неупругое сопротивление при нагружении гармонического типа определяется зависимостью [17]:
Ф(t) = (1+iγ)rz(t),(2.11)
где Ф(t), z(t) - усилие и перемещение, представляемое в комплексной форме; γ - коэффициент неупругого сопротивления; r -жесткость линейного осциллятора; i - мнимая единица i = √-1.
27
При формулировке зависимости (2.11) считается, что комплексные величины Ф и z определяются так, что их действительные части совпадают с реально принимаемыми физическими параметрами Ф и z, а их мнимые части являются комплексно сопряженными. В практических расчетах это отражается в том, что действительные части выражения (2.11) принимаются по косинусоидальному закону, а мнимые части - по синусоидальному.
В этих обозначениях дифференциальное уравнение движения системы с одной степенью свободы представляется в виде:
z.. (t)+(1+iγ) z(t)= - Δ.. (t)(2.12)
При этом предполагается, что заданная функция Δ(t) разлагается в ряд Фурье; этот ряд и сопряженный ему ряд Фурье образуют действительную и мнимую части комплексной переменной Δ..(t). Формально решения уравнений (2.10) и (2.12) оказываются похожими друг на друга. Решение уравнения (2.10) имеет вид:
z(t) = e -α t (C1 sin ω1 t + C2 cosω1 t) -
| - |
1 |
t∫0 |
Δ.. (τ)e-α(t-τ) sinω1 (t - ω) dτ |
| 1 |
(2.13)
где ω 1=√ω2 - α2.
Действительное решение комплексного уравнения (2.12) записывается в виде
z(t) = e
(C1 sin ω1 t + C2 cosω1 t) -
| - |
1 |
t∫0 |
Δ..(τ)e
sin ω1 (t - τ)dτ |
| ω1 |
(2.14)
Интегралы в (2.13) и (2.14), определяющие частные решения соответствующих дифференциальных уравнений, называются интегралами Дюамеля .
Эксперименты показывают, что коэффициенты α и γ имеют достаточно малые значения, поэтому с требуемой в практических расчетах точностью в выражениях (2.13) и (2.14) можно считать, что ω≈ω1≈ω, т.е. частота свободных колебаний системы с затуханием равна частоте свободных колебаний ее без затухания.
28
Нетрудно видеть, что при 2α = γω решения (2.13) и (2.14) совпадают. Это позволяет с равным основанием применять обе гипотезы при исследовании конкретной системы, характеристики которой определены опытным путем. Вместе с тем надо помнить, что гипотезы Фойгта и Е.С. Сорокина предполагают различие в составлении зависимостей между частотой колебаний и характеристиками затухания, что в случае системы со многими степенями свободы может привести к качественному различию результатов.
29
