1.3. Сейсмические волны. Распространение и отражение

Под сейсмическими волнами будем понимать совокупность различных типов волн, возникающих в очаге землетрясения, распространяющихся в толще земной поверхности и воздействующих на здания и сооружения в форме некоторого кинематического возбуждения, вызывающего их движение.

15

В теории упругости установлено, что в неограниченной упругой среде распространяется два типа волн - продольные и поперечные.

Продольные волны вызывают лишь деформации растяжения-сжатия по направлению нормали к фронту волны, в силу чего происходит изменение объема элемента среды. Эти волны, называемые в сейсмологии Р-волнами (primary wave - первичная волна), обладают наибольшей скоростью распространения, определяемой формулой:

где ρ, Е, ν - соответственно плотность, модуль упругости и коэффициент Пуассона материала среды.

Поперечные волны - S-волны (secondary wave - вторичные волны) характеризуются перемещениями частиц среды в направлении, перпендикулярном движению фронта волны. При этом возникают лишь деформации сдвига, сопровождаемые изменениями формы при неизменности объема элемента среды.

Скорость распространения поперечных волн определяется выражением:

Нетрудно видеть, что скорость распространения поперечных волн меньше скорости распространения продольных волн, так что их отношение

всегда больше единицы и зависит только лишь от значения коэффициента Пуассона материала среды.

Поперечная волна состоит из двух волн, одна из которых поляризована в вертикальной плоскости (SV-волна - vertical secondary), а вторая - в горизонтальной плоскости (SH-волна -horizontal secondary).

Отличительная черта распространения волн в неограниченной упругой среде состоит в том, что форма импульса начального возбуждения остается неизменной при движении волны.

В технической литературе для продольной волны часто употребляют термины - объемная или безвихревая, а для поперечных волн - волны искажения, вихревые или эквиволюмиальные. Заметим еще, что кривизна фронта волны обратно пропорциональна расстоянию от рассматриваемой точки до очага возбуждения. Поэтому при достаточно большом удалении от очага фронт волны может рассматриваться в виде плоскости - плоская волна.

16

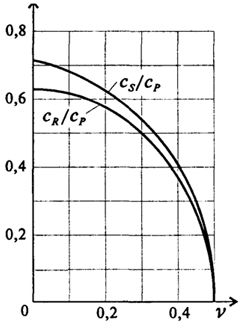
Рис. 1.5. Графики отношений скоростей распространения волн

В ограниченных упругих средах могут возникать и другие типы волн - волны Рэлея (R-волны) и волны Лява (L-волны). Амплитуды смещений, вызываемых этими волнами, очень быстро затухают по мере увеличения расстояния от свободной поверхности. Поэтому часто эти волны называют поверхностными.

Волны Рэлея поляризованы в вертикальном направлении, а волны Лява - в горизонтальном направлении, т.е. в волнах Рэлея частицы среды движутся вдоль, а в волнах Лява - перпендикулярно плоскости распространения волн.

Скорость распространения поверхностных волн Рэлея с_R меньше скоростей распространения Р и S-волн. Графики изменения

отношений C_s / C_p и C_R / C_р в зависимости от коэффициента Пуассона приведены на рис. 1.5.

Согласно существующим исследованиям [12] волны Рэлея несут большую часть энергии очага землетрясения; они вызывают поверхностные сотрясения и являются главной причиной разрушения сооружений.

Волны Лява возникают только при наличии слоистости среды, например, в двухслойной среде с различными параметрами плотности материала при условии, что скорость распространения поперечных волн в верхнем слое c _s ⁽²⁾ меньше, чем в нижнем c_s ⁽¹⁾.

Особое значение в задачах распространения волн имеют гармонические волны, когда перемещения частиц среды описываются выражением:

Здесь x ₁ - координата по направлению движения фронта волны; с - скорость волны; к - так называемое, волновое число, определяемое отношением частоты колебаний ω) к скорости с

где Т- период колебаний; λ = TC - длина волны.

Исследование вопроса распространения плоской гармонической волны показывает, что здесь могут иметь место два случая.

17

В первом случае скорость распространения волны не зависит от ее частоты, и тогда скорость эта называется фазовой. Характерной особенностью распространения волн в этом случае является то обстоятельство, что первоначально заданный импульс распространяется в среде без искажения.

Во втором случае скорость распространения волны зависит от ее частоты, и тогда картина движения отдельных групп волн усложняется. Если скорость волны повышается с увеличением периода (уменьшением частоты), то у "хвоста" группы волн образуются новые волны, в то время, как передние затухают и максимум волн в пределах группы передвигается все дальше назад. В противоположном случае волны с коротким периодом (короткие волны) бегут быстрее, чем волны с длинным периодом; у начала группы волн образуются новые волны, а на конце они исчезают. В этом случае максимум группы волн перемещается быстрее, чем максимумы отдельных волн.

Скорость, с которой перемещается максимум движения, называется групповой скоростью. Говорят, что в этом случае имеет место дисперсия, и волны называются дисперсионными.

Из числа типов рассмотренных волн продольные, поперечные и рэлеевские волны распространяются в среде без дисперсии, тогда как волны Лява являются дисперсионными.

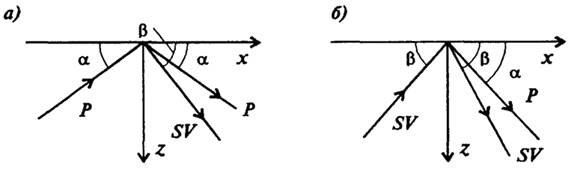
Рис. 1.6. Отражение волн от свободной поверхности

При падении плоских волн на свободную поверхность происходит явление отражения волн. На рис. 1.6,а показано отражение плоских монохроматических Р и SV волн от свободной поверхности. Видно, что падающая под углом α плоская Р-волна отражается от свободной поверхности, образуя две отраженные волны: Р-волну с углом отражения, равном углу падения, и SV-волну с углом отражения β.

Точно также при падении SV-волны под углом β получаем две отраженные волны SV и Р (рис. 1.6,6).

Закон отражения плоской волны определяется выражением:

18

Более подробное исследование явления отражения гармонических волн от свободной поверхности [12] показывает, что существуют критические углы падения Р и SV волн, при которых эти волны не отражаются.

Если Р-волна падает под углом α₁ =12°47' или α₂=30°, то эта волна не отражается, а распространяется вдоль поверхности. Точно так же при падающей SV-волне критическими углами падения являются β₁=55°41' или β₂=60°.

Аналогичная в качественном отношении картина имеет место и при падении волн на абсолютно жесткую поверхность.

В заключение отметим, что приведенные теоретические сведения о распространении и отражении волн находят широкое применение как в сейсмологии, так и в теории расчета сооружений на сейсмостойкость с учетом волнового характера сейсмического воздействия.

19