Для расчетов сооружений на воздействие акселерограмм будем исходить из уравнений движения (2.63), которые в принятых в данной главе обозначениях запишутся в виде
MZ..→ + CZ.→ +KZ→ = - MΔ..→(t).(4.21)
Будем считать, что вектор А представлен какой-либо заданной акселерограммой и в глобальной системе координат {х, у, z} является пространственным.
Тогда осевые компоненты вектора Δ..→(t) определяются следующим образом:
Δ..→x(t) = Δ..→(t)cos(Δ→,i→);
Δ..→y(t) = Δ..→(t)cos(Δ→,j→);
Δ..→z(t) = Δ..→(t)cos(Δ→,k→).
(4.22)
где Δ→ -вектор сейсмического воздействия; i→, j→, k→ -общепринятые обозначения ортов координатных осей.
Приведем вывод разрешающих уравнений, используемых для расчета системы с конечным числом степеней свободы на динамическое (сейсмическое) воздействие.
Как уже об этом говорилось, здесь используется метод разложения по собственным формам колебаний, или как еще его называют - метод модальной суперпозиции.
Считаем, что предварительно разрешена задача на собственные значения, т.е. вычислен спектр частот собственных колебаний и определены их формы (см. п. 4.4.2).
Представим искомый вектор перемещений Z→(t) в виде суперпозиций форм собственных колебаний:
Z→(t) = i=1∑n Viqi(t) = q→(t)
(4.23)
где qi(t)-как и выше (см. п. 2.5), представляет собой обобщенную координату, соответствующую i-ой форме собственных колебаний.
79
Подставляя (4.23) в (4.21) и умножая уравнение слева на V→iT, получаем
V→iTMVq..→+V→iTCV q.→+ V→iTKVq→= -V→iTMΔ..−(4.24)
Используя условия обобщенной ортогональности (4.16) и (4.19), имеем
V→iTMV = V→iTMV→i и V→iTKV = V→iTKV→i
Если заменить матрицу C = β1K + β2M по (4.5), то подставляя эти выражения в (4.24), получаем
Mi q..i + (β1Ki + β1Mi)q.i + Kiqi (4.25)
где Mi = V→iTMV→i-обобщенная масса для i-ой формы колебаний;
Ki = V→iTKV→i -обобщенная жесткость для i-ой формы колебаний;
Qi = V→iTMΔ..→ - обобщенная нагрузка для i-ой формы колебаний.
Обобщенную жесткость Ki, используя равенство (4.17), можно представить следующим образом
Ki = V→iTKV→i = ωi2V→iTMV→i = ωi2Mi(4.26)
Подставляя (4.26) в (4.25), получаем уравнение, полностью совпадающее с уравнением (2.64) и определяющее, как известно, уравнение движения системы с одной степенью свободы
q..i + 2ni q.i + ωi2 = - Qi(t)/Mi
(4.27)
где 2ni = β1ωi2 + β2
Коэффициент ni можно выразить через коэффициент неупругого сопротивления γ следующим образом:
Отсюда получаем
Здесь δ - логарифмический декремент колебаний.
Таким образом можно учесть частотно-независимое внутреннее трение, справедливое для большинства строительных конструкций. В первом приближении можно принять для стальных конструкций γ = 0,01, а для железобетонных - γ = 0,1.
80
Для решения уравнений (4.27) в программном комплексе "RADIUS" был использован метод Рунге-Кутта. Шаг по времени рекомендуется принимать равным Tmin/10, где Тmin - минимальный период учитываемых форм колебаний. В этом случае, как показали численные эксперименты, можно гарантировать получение точного и устойчивого решения.
Расчетная схема сооружений готовится так же, как и при расчете по нормам. Выбирается тип расчета - "динамика", а в ней -пиктограмма здания с сейсмическим воздействием.
Далее выбираются:
- KИ - максимальное число итераций, определяющее собственные векторы и числа;
- КЧ - число учитываемых форм колебаний;
- γ - коэффициент неупругого сопротивления материала (для железобетона - 0,1; стали - 0,01);
-dt- шаг интегрирования;
- αx - угол между направлением действия землетрясения и осью y:;
- αy - то же и осью у;
- NП - число пар (ti, z..i), определяющих акселерограмму землетрясения;
- ША - число, определяющее интервал выдачи результата на экран монитора и в файл результатов расчета;
- *k - множитель к ускорениям акселерограммы.
Затем задается акселерограмма парами чисел (ti, z..i), Для каждого последовательного пика, причем интервалы Δt на акселерограмме могут быть неодинаковыми. Следовательно, акселерограмму можно задавать только по ее пикам.
1. По исходным данным формируются матрицы М и К. По формулам (4.22) вычисляются компоненты вектора Δ..→.
2. Определяются частоты ωi и формы V→i собственных колебаний.
3. Определяются обобщенные массы Мi и обобщенные нагрузки Qi(t).
81
4. Решаются уравнения (4.27), и для всех форм колебаний находятся обобщенные координаты qi для каждого временного шага.
5. Для каждого временного шага по формуле (4.23) вычисляется вектор перемещений Z→(t)
6. Для каждого временного шага по формуле (4.2) вычисляются внутренние усилия для всех элементов.
7. На каждом временном шаге определяется норма перемещений. Для момента времени, соответствующего максимальной норме перемещений, выводятся на экран и в файл результатов эпюры внутренних усилий и соответствующее время. Предполагается, что именно в этот момент сооружение находится в наиболее опасном состоянии.
8. Строится выборка максимальных значений усилий по всем временным шагам для каждого расчетного сечения и строится соответствующая эпюра, которая выводится на экран монитора и печать. Учитывая, что максимальные значения усилий по каждой из форм достигаются в различные моменты времени, получаемая эпюра внутренних усилий не будет, конечно, отвечать условиям равновесия.
Отметим, что программа "RADIUS" расчета сооружений на сейсмические воздействия позволяет контролировать на экране монитора вводимую по точкам акселерограмму Δ→ и наблюдать анимационную кинограмму движения сооружения в процессе действия землетрясения. Кроме того, можно вывести на экран график движения любого узла по любой из шести степеней свободы и проследить его перемещение в процессе движения.
Такая возможность очень полезна как для учебных, так и исследовательских целей - изучение действия различных нагрузок, влияние демпфирования, околорезонансные явления, эффект сложения колебаний (биения, нарастание колебаний) и т.д.
В заключение рассмотрим три примера применения программного комплекса "RADIUS" к расчету сооружений на воздействие акселерограмм.
Пример 1. В качестве первого примера использовалась расчетная схема в виде трехмассового консольного стержня, рассмотренная ранее в п. 3.1 и п. 4.4 данного пособия.
В качестве воздействия была взята акселерограмма Спитакского землетрясения. Отцифровка записи этого землетрясения с временным шагом t = 0.05 с приведена в таблице 4.1.
Для расчета использовался отрезок этой акселерограммы с 7.0 с до 12 с, т.е. самая существенная ее часть. Считая t = 7.0 с за условный нуль, принимались нулевые начальные условия.
На рис. 4.18 показан кадр кинограммы перемещений, соответствующий максимальной норме перемещений при tусл = 3.1 с; вверху показана сама консоль, внизу - расчетная акселерограмма.
82
На рис. 4.19 показана эпюра изгибающих моментов, соответствующая tусл = 3.1 с.
Как отмечалось ранее, максимальные усилия в сечениях возникают в различные моменты времени; поэтому выборка (рис. 4.20) существенно отличается от эпюры на рис. 4.19.
На рис. 4.21 представлены графики изменения во времени действующей нагрузки на фоне акселерограммы и перемещения верхней точки консоли по оси х.
Пример 2. В качестве второго примера была выбрана расчетная схема, использованная в п. 3.2 данного пособия. Сейсмическое воздействие задавалось точно так же, как и в предыдущем примере.
На рис. 4.22 - 4.24 представлены некоторые результаты расчета данной конструкции на воздействие заданной акселерограммы, аналогичные приведенным выше.
На рис. 4.22 показан график перемещений конструкции в момент, когда норма перемещений достигает максимального значения (tусл = 3.1 с). На рис. 4.23 приведена соответствующая эпюра изгибающих моментов, а на рис. 4.24 представлены графики изменения во времени действующей сейсмической нагрузки на фоне акселерограмм и перемещений верхней точки консоли.
Сравнение результатов расчета по СНиП II-7-81 и акселерограмме Спитакского землетрясения показало, что моменты в опорном сечении отличаются для примера 1 в 160000/25430 = 5,3 раза; для примера 2 в 3835,7/1240,1 =3,1раза. Это подтверждает тот факт, что расчеты по реальным акселерограммам дают результаты, превышающие результаты расчета по СНиП II-7-81, более чем в 2раза.
83
Таблица 4.1
| t(с) |
Δ..ñì2 |
t(с) |
Δ..ñì2 |
t(с) |
Δ..ñì2 |
t(с) |
Δ..ñì2 |
| 0.00 |
16.3 |
1.45 |
8.0 |
2.90 |
-4.3 |
4.35 |
8.5 |
| 0.05 |
9.7 |
1.50 |
-6.3 |
2.95 |
-9.2 |
4.40 |
1.3 |
| 0.10 |
-24.1 |
1.55 |
-20.9 |
3.00 |
-3.2 |
4.45 |
-4.1 |
| 0.15 |
-22.4 |
1.60 |
-9.5 |
3.05 |
2.5 |
4.50 |
-32.7 |
| 0.20 |
13.0 |
1.65 |
-2.6 |
3.10 |
2.0 |
4.55 |
-14.3 |
| 0.25 |
10.2 |
1.70 |
-10.7 |
3.15 |
-0.2 |
4.60 |
11.7 |
| 0.30 |
3.2 |
1.75 |
-13.4 |
3.20 |
8.4 |
4.65 |
6.3 |
| 0.35 |
-9.8 |
1.80 |
-22.1 |
3.25 |
0.3 |
4.70 |
12.5 |
| 0.40 |
-4.1 |
1.85 |
-14.1 |
3.30 |
-6.3 |
4.75 |
-5.3 |
| 0.45 |
-8.0 |
1.90 |
5.4 |
3.35 |
-20.2 |
4.80 |
-10.7 |
| 0.50 |
12.3 |
1.95 |
17.5 |
3.40 |
-27.6 |
4.85 |
-13.4 |
| 0.55 |
13.5 |
2.00 |
12.3 |
3.45 |
-15.2 |
4.90 |
-37.2 |
| 0.60 |
-2.9 |
2.05 |
-13.7 |
3.50 |
-3.0 |
4.95 |
-11.4 |
| 0.65 |
-10.6 |
2.10 |
-16.0 |
3.55 |
-0.5 |
5.00 |
2.9 |
| 0.70 |
-14.1 |
2.15 |
-19.4 |
3.60 |
5.2 |
5.05 |
27.3 |
| 0.75 |
0.2 |
2.20 |
-24.6 |
3.65 |
34.7 |
5.10 |
15.6 |
| 0.80 |
6.4 |
2.25 |
6.5 |
3,70 |
51.8 |
5.15 |
41.2 |
| 0.85 |
21.9 |
2.30 |
22.3 |
3.75 |
36.8 |
5.20 |
30.1 |
| 0.90 |
7.7 |
2.35 |
-1.1 |
3.80 |
15.4 |
5.25 |
15.0 |
| 0.95 |
-3.3 |
2.40 |
-10.8 |
3.85 |
0.9 |
5.30 |
16.3 |
| 1.00 |
-15.8 |
2.45 |
-19.0 |
3.90 |
-19.5 |
5.35 |
-5.5 |
| 1.05 |
-14.5 |
2.50 |
17.3 |
3.95 |
-2.3 |
5.40 |
-18.3 |
| 1.10 |
9.4 |
2.55 |
-14.5 |
4.00 |
11.1 |
5.45 |
-29.2 |
| 1.15 |
34.2 |
2.60 |
2.7 |
4.05 |
20.6 |
5.50 |
5.3 |
| 1.20 |
16.4 |
2.65 |
-9.7 |
4.10 |
6.1 |
5.55 |
-4.0 |
| 1.25 |
9.0 |
2.70 |
-2.1 |
4.15 |
-17.5 |
5.60 |
-1.2 |
| 1.30 |
-4.5 |
2.75 |
4.4 |
4.20 |
-58.3 |
5.65 |
-15.0 |
| 1.35 |
-21.8 |
2.80 |
7.3 |
4.25 |
-51.5 |
5.70 |
2.4 |
| 1.40 |
-5.6 |
2.85 |
3.6 |
4.30 |
-23.2 |
5.75 |
12.6 |
84
Продолжение табл. 4.1
| t(с) |
Δ..ñì2 |
t(с) |
Δ..ñì2 |
t(с) |
Δ..ñì2 |
t(с) |
Δ..ñì2 |
| 5.80 |
18.4 |
7.25 |
8.9 |
8.70 |
63.7 |
10.15 |
44.9 |
| 5.85 |
9.3 |
7.30 |
14.1 |
8.75 |
78.2 |
10.20 |
-38.2 |
| 5.90 |
10.6 |
7.35 |
22.7 |
8.80 |
43.1 |
10.25 |
0.3 |
| 5.95 |
2.1 |
7.40 |
6.6 |
8.85 |
11.2 |
10.30 |
-86.3 |
| 6.00 |
-3.0 |
7.45 |
-34.0 |
8.90 |
-9.6 |
10.35 |
-74.7 |
| 6.05 |
-9.1 |
7.50 |
-50.1 |
8.95 |
52.7 |
10.40 |
-80.5 |
| 6.10 |
-5.7 |
7.55 |
28.8 |
9.00 |
128.3 |
10.45 |
-25.1 |
| 6.15 |
-25.6 |
7.60 |
-13.0 |
9.05 |
103.5 |
10.50 |
132.2 |
| 6.20 |
-4.5 |
7.65 |
-21.2 |
9.10 |
92.4 |
10.55 |
-54.0 |
| 6.25 |
6.9 |
7.70 |
-3.7 |
9.15 |
51.6 |
10.60 |
7.0 |
| 6.30 |
18.3 |
7.75 |
-9.2 |
9.20 |
-4.7 |
10.65 |
-19.3 |
| 6.35 |
28.1 |
7.80 |
-35.5 |
9.25 |
-88.9 |
10.70 |
-4.9 |
| 6.40 |
23.2 |
7.85 |
-29.1 |
9.30 |
-201.7 |
10.75 |
-23.4 |
| 6.45 |
25.7 |
7.90 |
-2.3 |
9.35 |
-283.3 |
10.80 |
-1.2 |
| 6.50 |
17.6 |
7.95 |
22.3 |
9.40 |
-290.4 |
10.85 |
-36.5 |
| 6.55 |
7.9 |
8.00 |
34.7 |
9.45 |
-13.5 |
10.90 |
-71.3 |
| 6.60 |
-0.6 |
8.05 |
70.4 |
9.50 |
-54.0 |
10.95 |
-4.8 |
| 6.65 |
1.2 |
8.10 |
109.3 |
9.55 |
-113.3 |
11.00 |
52.3 |
| 6.70 |
-3.8 |
8.15 |
19.5 |
9.60 |
-50.5 |
11.05 |
-10.5 |
| 6.75 |
-11.7 |
8.20 |
-9.4 |
9.65 |
43.2 |
11.10 |
72.3 |
| 6.80 |
-20.1 |
8.25 |
-20.3 |
9.70 |
83.7 |
11.15 |
34.6 |
| 6.85 |
-15.6 |
8.30 |
-34.6 |
9.75 |
12.8 |
11.20 |
-2.0 |
| 6.90 |
3.8 |
8.35 |
-1.2 |
9.80 |
220.9 |
11.25 |
-20.9 |
| 6.95 |
9.6 |
8.40 |
37.2 |
9.85 |
234.0 |
11.30 |
-67.1 |
| 7.00 |
-8.5 |
8.45 |
48.7 |
9.90 |
38.8 |
11.35 |
-8.3 |
| 7.05 |
-15.2 |
8.50 |
-0.2 |
9.95 |
-20.3 |
11.40 |
15.о |
| 7.10 |
-6.8 |
8.55 |
-54.1 |
10.00 |
-79.5 |
11.45 |
-16.3 |
| 7.15 |
8.1 |
8.60 |
-29.7 |
10.05 |
-43.7 |
11.50 |
15.5 |
| 7.20 |
29.3 |
8.65 |
2.3 |
10.10 |
-58.0 |
11.55 |
-19.9 |
85
Продолжение табл. 4.1
| t(с) |
Δ..ñì2 |
t(с) |
Δ..ñì2 |
t(с) |
Δ..ñì2 |
t(с) |
Δ..ñì2 |
| 11.60 |
4.0 |
13.05 |
-11.4 |
14.50 |
0.2 |
15.95 |
15.4 |
| 11.65 |
-27.4 |
13.10 |
-28.1 |
14.55 |
12.3 |
16.00 |
12.1 |
| 11.70 |
23.2 |
13.15 |
-15.6 |
14.60 |
19.6 |
16.05 |
5.2 |
| 11.75 |
19.6 |
13.20 |
-3.9 |
14.65 |
15.4 |
16.10 |
-1.7 |
| 11.80 |
66.6 |
13.25 |
-5.8 |
14.70 |
25.7 |
16.15 |
-7.8 |
| 11.85 |
37.4 |
13.30 |
7.6 |
14.75 |
23.7 |
16.20 |
-15.4 |
| 11.90 |
51.1 |
13.35 |
15.3 |
14.80 |
11.9 |
16.25 |
-17.6 |
| 11.95 |
11.8 |
13.40 |
12.4 |
14.85 |
15.1 |
16.30 |
-9.3 |
| 12.00 |
20.8 |
13.45 |
23.2 |
14.90 |
5.6 |
16.35 |
-2.2 |
| 12.05 |
-92.7 |
13.50 |
13.1 |
14.95 |
-4.1 |
16.40 |
4.1 |
| 12.10 |
-41.5 |
13.55 |
15.8 |
15.00 |
-13.7 |
16.45 |
3.8 |
| 12.15 |
13.3 |
13.60 |
1.4 |
15.05 |
-25.8 |
16.50 |
8.7 |
| 12.20 |
38.7 |
13.65 |
-8.9 |
15.10 |
-1.6 |
16.55 |
16.1 |
| 12.25 |
17.6 |
13.70 |
-15.0 |
15.15 |
5.3 |
16.60 |
11.5 |
| 12.30 |
-7.9 |
13.75 |
-7.1 |
15.20 |
12.1 |
16.65 |
3.0 |
| 12.35 |
23.5 |
13.80 |
-26.3 |
15.25 |
-0.3 |
16.70 |
-3.7 |
| 12.40 |
19.8 |
13.85 |
-39.0 |
15.30 |
-17.2 |
16.75 |
-8.2 |
| 12.45 |
8.5 |
13.90 |
-5.7 |
15.35 |
-9.3 |
16.80 |
-12.4 |
| 12.50 |
41.2 |
13.95 |
6.0 |
15.40 |
5.7 |
16.85 |
-12.8 |
| 12.55 |
37.8 |
14.00 |
11.5 |
15.45 |
3.8 |
16.90 |
-13.1 |
| 12.60 |
75.5 |
14.05 |
19.0 |
15.50 |
9.7 |
16.95 |
-7.5 |
| 12.65 |
41.4 |
14.10 |
7.1 |
15.55 |
-1.4 |
17.00 |
-0.3 |
| 12.70 |
12.1 |
14.15 |
13.0 |
15.60 |
-2.5 |
17.05 |
2.9 |
| 12.75 |
0.8 |
14.20 |
1.2 |
15.65 |
9.6 |
17.10 |
9.3 |
| 12.80 |
23.7 |
14.25 |
-5.7 |
15.70 |
4.7 |
17.15 |
10.7 |
| 12.85 |
15.8 |
14.30 |
-10.1 |
15.75 |
-5.9 |
17.20 |
4.3 |
| 12.90 |
2.1 |
14.35 |
-9.0 |
15.80 |
-8.1 |
17.25 |
-2.1 |
| 12.95 |
-5.7 |
14.40 |
-22.3 |
15.85 |
-3.2 |
17.30 |
-8.8 |
| 13.00 |
-13.1 |
14.45 |
-14.7 |
15.90 |
6.3 |
17.35 |
-13.6 |
86
Продолжение табл. 4.1
| t(с) |
Δ..ñì2 |
t(с) |
Δ..ñì2 |
t(с) |
Δ..ñì2 |
t(с) |
Δ..ñì2 |
| 17.40 |
-7.3 |
18.10 |
-16.4 |
18.80 |
-14.8 |
19.50 |
-21.3 |
| 17.45 |
-2.1 |
18.15 |
-4.7 |
18.85 |
-4.4 |
19.55 |
-16.5 |
| 17.50 |
5.8 |
18.20 |
8.5 |
18.90 |
12.1 |
19.60 |
-7.0 |
| 17.55 |
10.1 |
18.25 |
20.1 |
18.95 |
14.3 |
19.65 |
-1.2 |
| 17.60 |
25.1 |
18.30 |
28.3 |
19.00 |
8.2 |
19.70 |
8.0 |
| 17.65 |
28.4 |
18.35 |
36.1 |
19.05 |
28.3 |
19.75 |
3.4 |
| 17.70 |
25.9 |
18.40 |
29.9 |
19.10 |
21.3 |
19.80 |
9.9 |
| 17.75 |
14.3 |
18.45 |
42.3 |
19.15 |
18.5 |
19.85 |
7.3 |
| 17.80 |
-3.5 |
18.50 |
18.1 |
19.20 |
4.2 |
19.90 |
7.8 |
| 17.85 |
-8.7 |
18.55 |
6.4 |
19.25 |
-2.3 |
19.95 |
3.2 |
| 17.90 |
-16.3 |
18.60 |
-0.7 |
19.30 |
-9.6 |
20.00 |
-1.3 |
| 17.95 |
-20.8 |
18.65 |
-8.9 |
19.35 |
-7.3 |
|
|
| 18.00 |
-43.7 |
18.70 |
-23.7 |
19.40 |
-15.4 |
|
|
| 18.05 |
-31.2 |
18.75 |
-24.5 |
19.45 |
-23.2 |
|
|
Поэтому для особо ответственных сооружений и высоких зданий нормы СНиП II-7-81 предписывают проводить расчет как по нормам, так и по акселерограмма, подобранным для соответствующих районов и грунтов.
Пример 3. В качестве третьего примера рассчитана железобетонная двухпролетная пространственная рама с несимметрично расположенными в ее узлах массами (рис. 4.25). Проведено два расчета.
Первый по нормам на 9 баллов в направлении оси х. На рис. 4.25 показана первая форма колебаний и соответствующие сейсмические силы.
Второй расчет - на акселерограмму землетрясения в Эль Центре (1949г.), заданную 100 парами точек. На рис. 4.26 выведен 1 кадр кинограммы перемещений рамы, внизу - заданная акселерограмма. На рис. 4.27 показан график перемещения узла 12 по оси х.
87
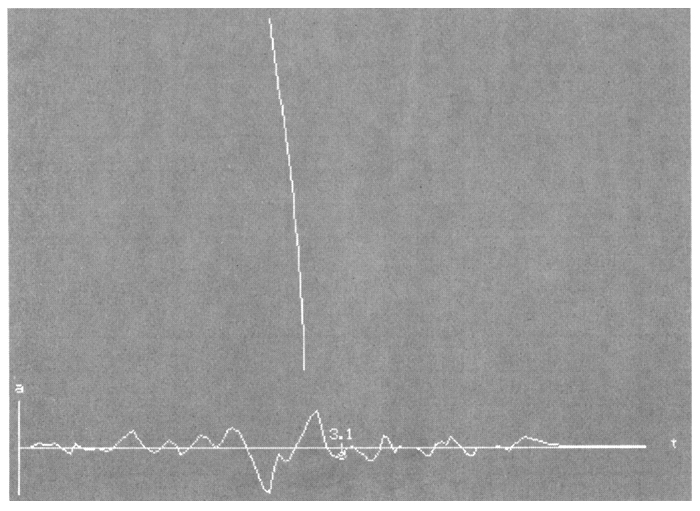
Рис. 4.18. Кадр кинограммы премещений консоли при t
усл=3.11 с
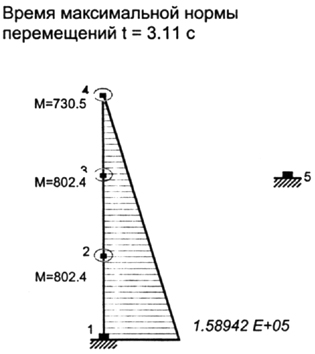
Рис. 4.19 Эпюра изгибающих моментов при t
усл=3.11 с
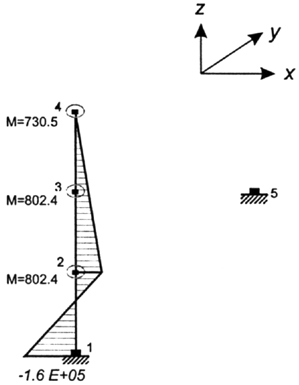
Рис. 4.20 Выборка максимальных моментов
88

Рис. 4.21. Графики изменения во времени действующей нагрузки
и перемещение верхней точки консоли
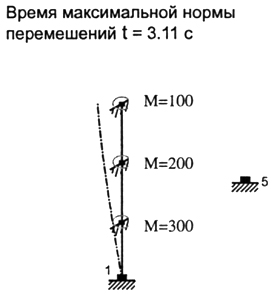
Рис. 4.22. Эпюра перемещений при t
усл =3.11 с
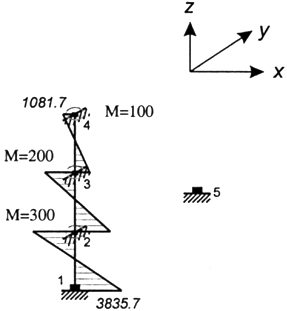
Рис. 4.23. Эпюра изгибающих моментов при t
усл =3.11 с
89

Рис. 4.24. Графики изменения во времени действующей нагрузки
и перемещение верхней точки консоли

Рис. 4.25. Первая форма собственных колебаний рамы и сейсмические силы
90
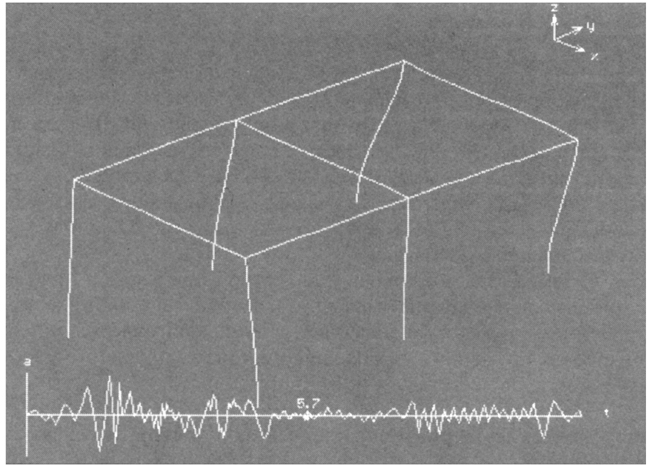
Рис. 4.26. Кадр кинограммы перемещений для
t =5.8 с
и акселерограмма землетрясения Эль Центре (1949г.) и
перемещение верхней точки консоли
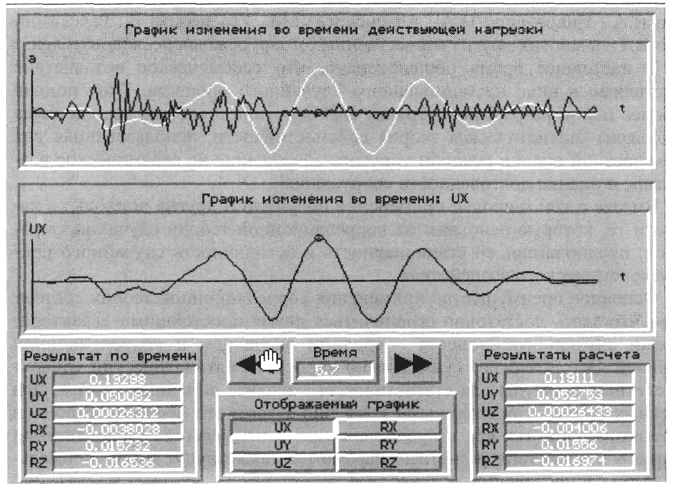
Рис. 4.27. График перемещения узла 12 в направлении оси
x
91
