Здесь приведены примеры определения частот и форм собственных колебаний балки и плоской рамы с помощью программы "RADIUS". Примеры были подобраны так, чтобы, с одной стороны, протестировать результаты расчета, получаемые по программе "RADIUS", и убедиться в их достоверности, а с другой стороны, проиллюстрировать возможности этой программы в задачах определения частот и форм собственных колебаний.
Кроме того заметим, что перед любым динамическим расчетом, вообще говоря, рекомендуется определять частоты и формы собственных колебаний с тем, чтобы проверить правильность модели конструкции, оценить порядок частот и установить геометрическую адекватность форм колебаний рассматриваемой конструкции.
Пример 1. Для шарнирно опертой балки длиной l, спектр частот определяется следующим аналитическим выражением:
где п - номер частоты, т - погонная масса.
Примем l = π, E = J = m= 1, тогда ωn = п2. Таким образом, точные значения собственных частот колебаний известны.
Применяя программу "RADIUS", разобьем сначала балку на 16 участков. Вычисления дают следующие результаты:
ω1 = 1,0001 с-1;
... ...
ω4=15,996 с-1;
... ...
ω9 = 79,935 с-1.*
... ...
Теперь нетрудно оценить погрешность полученных решений. Наибольшая погрешность в данном случае получается при вычислении ω9 (Δ=1,31%). Вычисленные формы собственных колебаний приведены на рис. 4.4 - 4.6. (экранные распечатки).
68
| Круговая частота |
: |
1.0001 рад/с |
|
| Период |
: |
6.2825 с |
|
| Техническая частота |
: |
0.1591 Гц |
|
| Число интераций |
: |
5 |
|
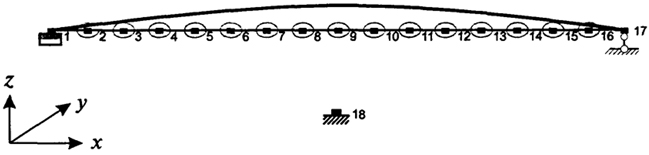
Рис. 4.4. Форма собственных колебаний балки при
n=1 (16 участков)
| Круговая частота |
: |
15.996 рад/с |
|
| Период |
: |
0.39279 с |
|
| Техническая частота |
: |
2.5459 Гц |
|
| Число интераций |
: |
100 |
|

Рис. 4.5. Форма собственных колебаний балки при
n=4 (16 участков)
| Круговая частота |
: |
78.835 рад/с |
|
| Период |
: |
0.078604 с |
|
| Техническая частота |
: |
12.722 Гц |
|
| Число интераций |
: |
100 |
|

Рис. 4.6. Форма собственных колебаний балки при
п=9 (16 участков)
69
При разбиении балки на четыре участка, вычисления по программе "RADIUS" дают следующие результаты:
ω1 = 0,99977 с-1;
ω2 = 3,9713 с-1;
ω3 = 8,4319 с-1.
Соответствующие формы собственных колебаний приведены на рис. 4.7 - 4.9.
Анализ полученных данных подтверждает уже известный факт, что точность результатов вычислений возрастает с увеличением степени дискретизации конструкции.
Вместе с тем, при вычислении низших частот даже достаточно грубая дискретизация дает удовлетворительные результаты. Вычисления по программе "RADIUS" показали, что сложные и крупные сооружения, состоящие из большого количества элементов, нет нужды делить на еще более мелкие элементы, так как стягивание распределенных масс в узлы сооружения позволяет получать практически точные результаты по первым частотам и формам. Если же необходим учет высших форм, то стержневые элементы требуют дополнительного разбиения путем введения дополнительных узлов.
Пример 2. В этом примере рассматривалась плоская П-образная рама с сосредоточенными массами М= 100, расположенными в узлах рамы. Исследовались пространственные колебания этой рамы. На рис. 4.10-4.15 показаны первые шесть форм собственных колебаний рамы; здесь же приведены значения круговых и технических частот.
Наиболее примечательным здесь является то обстоятельство, что в пространственной постановке наименьшая частота соответствует колебаниям "из плоскости" рамы, тогда как плоскостному расчету соответствует вторая частота (рис. 4.11).
Третья форма колебаний П-образной рамы (см. рис. 4.12) определяет крутильные колебания; четвертая форма (см. рис. 4.13) -осевые колебания. Последующие две формы (см. рис. 4.14 и рис. 4.15) можно определить как формы изгибно-осевые.
Заметим, что полученные результаты существенно отличаются от результатов привычного плоскостного расчета рассматриваемой рамы. Это объясняется спецификой программы "RADIUS", учитывающей осевые перемещения элементов и пространственный характер колебаний.
70
| Круговая частота |
: |
0.99977 рад/с |
|
| Период |
: |
6.2846 с |
|
| Техническая частота |
: |
0.15912 Гц |
|
| Число интераций |
: |
5 |
|
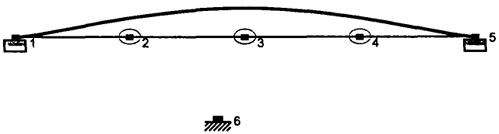
Рис. 4.7. Форма собственных колебаний балки при
п=1 (4 участка)
| Круговая частота |
: |
3.9713 рад/с |
|
| Период |
: |
1.5822 с |
|
| Техническая частота |
: |
0.63205 Гц |
|
| Число интераций |
: |
23 |
|
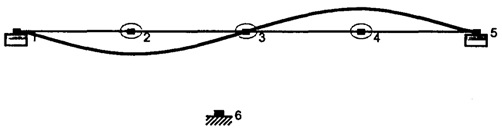
Рис. 4.8. Форма собственных колебаний балки при
п=2 (4 участка)
| Круговая частота |
: |
8.4319 рад/с |
|
| Период |
: |
4.1133 с |
|
| Техническая частота |
: |
1.342 Гц |
|
| Число интераций |
: |
3 |
|
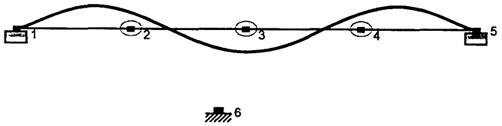
Рис. 4.9. Форма собственных колебаний балки при
n=3 (4 участка)
71
| Круговая частота |
: |
1.5275 рад/с |
|
| Период |
: |
4.1133 с |
|
| Техническая частота |
: |
0.24311 Гц |
|
| Число интераций |
: |
100 |
|
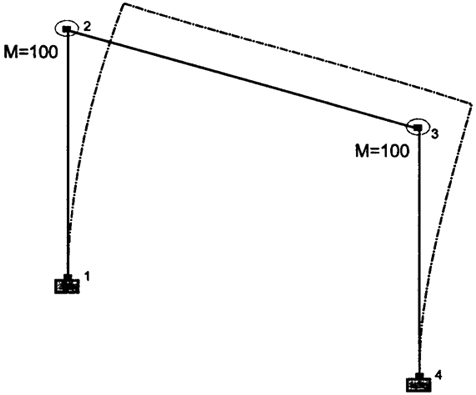
Рис. 4.10. Первая форма собственных колебаний рамы
| Круговая частота |
: |
2.5299 рад/с |
|
| Период |
: |
2.4934 с |
|
| Техническая частота |
: |
0.40105 Гц |
|
| Число интераций |
: |
100 |
|
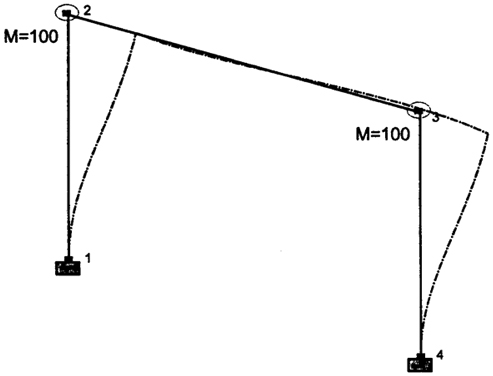
Рис. 4.11. Вторая форма собственных колебаний рамы
72
| Круговая частота |
: |
2.4234 рад/с |
|
| Период |
: |
2.5927 с |
|
| Техническая частота |
: |
0.3857 Гц |
|
| Число интераций |
: |
4 |
|
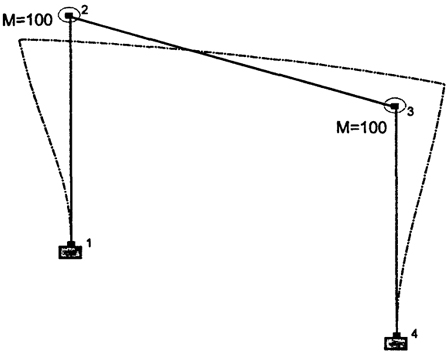
Рис. 4.12. Третья форма собственных колебаний рамы
| Круговая частота |
: |
69.282 рад/с |
|
| Период |
: |
0.09069 с |
|
| Техническая частота |
: |
11.027 Гц |
|
| Число интераций |
: |
13 |
|
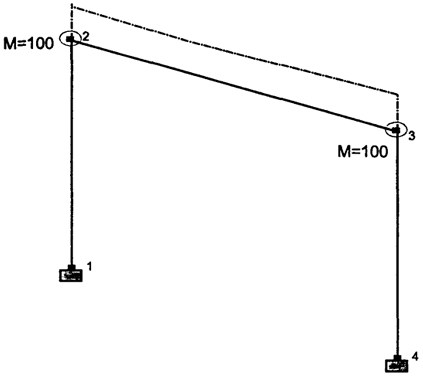
Рис. 4.13. Четвертая форма собственных колебаний рамы
73
| Круговая частота |
: |
69.324 рад/с |
|
| Период |
: |
0.090635 с |
|
| Техническая частота |
: |
11.033 Гц |
|
| Число интераций |
: |
48 |
|
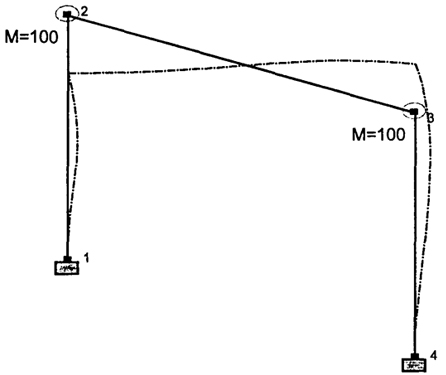
Рис. 4.14. Пятая форма собственных колебаний рамы
| Круговая частота |
: |
92.97 рад/с |
|
| Период |
: |
0.067579 с |
|
| Техническая частота |
: |
14.798 Гц |
|
| Число интераций |
: |
100 |
|
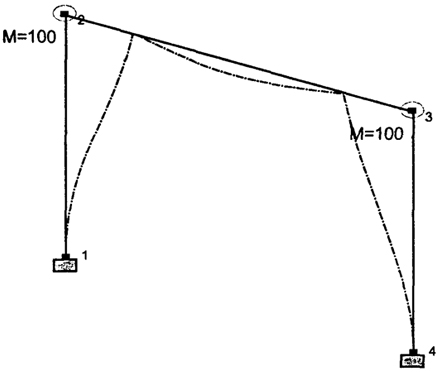
Рис. 4.15. Шестая форма собственных колебаний рамы
74
*
Здесь имеются ввиду круговые частоты колебаний, для которых размерность, строго говоря, определяется в виде рад/с. 68
