4.2.2. Матрица жесткости конечных элементов

В учебном пособии [25] подробно описана процедура построения матрицы жесткости К_т для различных плоских стержневых элементов, осуществляемая по формулам:

где А - статическая матрица, устанавливающая связь между усилиями S_m в элементах системы и внешними узловыми силами Р, В-матрица деформаций, устанавливающая связь между деформациями элементов и перемещениями узлов; она может трактоваться как матрица перехода из локальной системы координат в глобальную; k - матрица внутренней жесткости системы, устанавливающая связь между деформациями и усилиями элементов конструкции.

Не давая подробного вывода этих матриц, укажем лишь на то, что для каждого узла элемента в пространстве вводится по три линейных и по три угловых перемещения (линейные смещения и углы поворота). В силу этого для балочного элемента с защемленными концами матрица К_т имеет размер 12x12.

В качестве исходных данных задают площадь поперечного сечения, моменты инерции относительно двух главных осей поперечного сечения и момент инерции на кручение.

63

Задаются также значения модуля упругости Е и модуля сдвига G. Для однозначной ориентации стержневого элемента в пространстве кроме начального i-го и конечного j-го узлов задают также третий узел - k-ый, определяющий плоскость ijk. Очевидно, точка k не должна лежать на линии i-j (рис. 4.2).

Узел k может быть узлом конструкции или каким-либо дополнительным узлом, при условии, что описание элемента осуществляется по часовой стрелке: i→j→k; тогда эпюры моментов будут откладываться со стороны растянутых волокон. Моменты инерции J₁, J₂, J₃ - есть момент инерции на кручение и моменты инерции относительно осей 2 и 3.

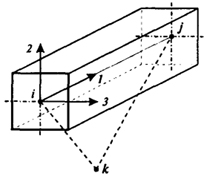
Рис. 4.2. Описание элемента

64