В настоящее время МКЭ занимает главенствующее положение в области программных комплексов, предназначенных для расчета сооружений на прочность, устойчивость и колебания. В свое время на кафедре "Строительная механика" МГСУ под руководством С.Б. Синицына была разработана программа "RADIUS", основанная на использовании МКЭ [25], которая, будучи приспособлена для учебных целей, позволяла вместе с тем решать и широкий спектр задач прочности, устойчивости (в т.ч. деформационного расчета) и динамики стержневых систем.
При решении динамических задач в программном комплексе "RADIUS" был использован метод разложения по собственным формам колебаний. Это обстоятельство в значительной степени способствовало возможности приспособления этой программы к расчету сооружений на сейсмические воздействия, причем как по нормативному методу, так и на воздействия заданных акселерограмм.
Исходя из чисто методологических соображений, в данной главе будем использовать обозначения, принятые в учебном пособии [25]. В отдельных случаях, по мере необходимости, будет указана взаимосвязь с ранее использованными обозначениями.
Прежде всего, остановимся на проблеме дискретизации, являющейся основой метода конечных элементов.
Напомним некоторые основные положения МКЭ [25], необходимые для дальнейшего изложения.
При решении задач с помощью МКЭ числом степеней свободы называют число неизвестных перемещений узлов системы (линейных и угловых). Узлами принято назначать точки объединения стержневых элементов, опоры, точки скачкообразного изменения жесткости, а также любые точки элементов, перемещения которых необходимо определить (рис. 4.1). При таком подходе каждый элемент является стержнем с шарнирными или защемленными концами.
Например, для рамы, показанной на рис. 4.1, число степеней свободы будет равно:
n = 3У - C0 = 3·7 - 6 = 15
Здесь n - число степеней свободы; У- число узлов, включая опорные; С0 - число опорных стержней.
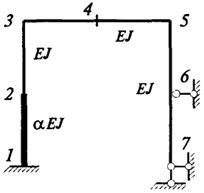
Рис. 4.1. Расчетная
схема рамы
61
В динамических задачах числом степеней свободы называют число степеней свободы масс, расположенных на конструкции. Для системы, состоящей из жестких дисков, числа динамических и статических степеней свободы совпадают, так как положение каждого жесткого диска однозначно определяет положение всех масс, расположенных на нем.
Системы, состоящие из гибких элементов, обладают массами, распределенными по их длине. Поэтому, строго говоря, эти системы имеют бесконечное число степеней свободы. Для практических расчетов такие элементы обычно аппроксимируют элементами с конечным числом сосредоточенных масс. При этом точность расчетов возрастает с увеличением числа сосредоточенных масс.
При составлении расчетной схемы МКЭ важно учесть все геометрические и физические параметры системы: опорные закрепления, правильное распределение жесткостей - определение площадей и моментов инерции элементов (для пространственных элементов - моменты инерции на кручение и моменты инерции на изгиб в двух плоскостях).
Особое внимание следует обратить на выбор системы единиц, поскольку неудачный выбор ее может повлиять на результаты расчета. В современных расчетах строительных конструкций получила официальное признание и сертификацию модифицированная система единиц СИ, когда исходные данные задаются в следующем виде: нагрузки - кН, кН·м; линейные размеры - м; площади поперечных сечений - м2; моменты инерции - м4; массы - т; ускорения - м/с2.
Тогда результаты расчетов будут исчисляться: перемещения - м; усилия - кН, кН·м; частоты – с-1.
62
