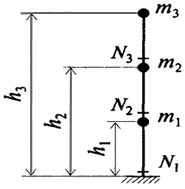
Рис. 3.1. Расчетная схема
В качестве примера расчета было выбрано реальное трехэтажное здание. Расчетная схема принималась в виде консольного стержня с массами, сосредоточенными в уровнях перекрытий и покрытия (рис. 3.1), т.е. в виде трехмассовой системы:
m 1= m2=802,4т;
m3=730,5т.
Высота этажа принималась равной 8,25 м. Тогда h1 = 8,25 м; h2 = 16,5 м; h 3 = 24,75 м .
Модуль упругости консольного стержня: EJ=19,321¸107Кн·м2.
Здесь же на рис. 3.1 показаны расчетные сечения, для которых надлежит вычислить значения внутренних усилий.
Собственные частоты определяем с помощью векового уравнения, получаемого из определителя
| (δ11m1 - λ) |
δ12m2 |
δ13m3 |
| δ21m1 |
(δ22m2 -λ) |
δ23m3 |
| δ31m1 |
δ32m2 |
(δ33m3 -λ) |
= 0 (3.1)
Коэффициенты матрицы податливости λik можно определять известным способом путем "перемножения" эпюр изгибающих моментов, построенных для консольного стержня от действия единичных значений сил
Si= 1 (i=1,2,3).
В этом случае для вычисления коэффициента λik могут быть рекомендованы следующие формулы:
- при i = j δii = (hi) 3/ 3 EJ;
| - при i < j δii = |
hi |
[2 hi hj + hi(hj - hi)] |
| 6 EJ |
| - при i > j δii = |
hi |
[2 hi hj + hi(hj - hi)] |
| 6 EJ |
(3.2)
48
Подсчитывая эти коэффициенты, получаем следующую матрицу податливости (м/Н):
Раскрывая определитель (3.1), получаем кубическое уравнение относительно параметра А,
L = δ =
| 9,678·10-10 |
2,422·10-9 |
3,875·10-9 |
| 2,422·10-9 |
7,75·10-9 |
1,356·10-8 |
| 3,875·10-9 |
1,356·10-8 |
2,616·10-8 |
(3.3)
Раскрывая определитель (3.1), получаем кубическое уравнение относительно параметра λ
a3λ3 - a2λ2 + a1λ + a0 = 0
(3.4)
где а0 = 1,39·10-9; а1= 1,811·10-5; a2 = 0,026; a3= 1.
Решая уравнение (3.4), находим
λ1 = 0,025;
λ2= 6,233·10-4;
λ3= 8,781·10-5.
Тогда собственные частоты, определяемые по формуле ωi = √1/λi; оказываются равными (рад/с):
ω1 = 6,276;
ω2= 40,056;
ω3= 106,714.
Соответствующие периоды собственных колебаний, вычисляемые по формуле Ti = 2π/ωi (с.), равны
T1 =1,0;
T2=0,157;
T3 =0,059.
Вычисляя собственные векторы матрицы (3.1), находим
V→1T={0,157 0,533 1,0}
V→2T={-1,172 -1,364 1,0}
V→3T={4,212 -2,951 1,0}
Формы собственных колебаний, соответствующие этим векторам, показаны на рис. 3.2.
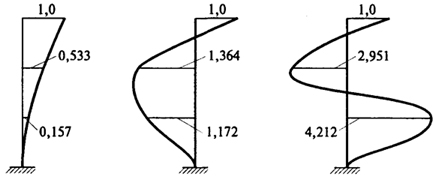
Рис. 3.2 Формы собственных колебаний
49
По формуле (2.75) подсчитываем нормированные коэффициенты форм ηik. Например,
| η11 = |
0,157(802,4·0,157+802,4·0,533+730,5·1,0 |
= 0,206 |
| 802,4·0,1572+802,4·0,5332+730,5·1,02 |
и т.д. Матрица нормированных коэффициентов форм колебаний приведена ниже:
η =
| 0,206 |
0,406 |
0,334 |
| 0,699 |
0,535 |
-0,234 |
| 1,313 |
-0,392 |
0,073 |
(3.6)
Вычисленные значения нормированных коэффициентов форм, как нетрудно убедиться, удовлетворяют условию (2.76).
50
