Для решения системы уравнений (2.38) или (2.39) используем известный в динамике сооружений метод представления решения в виде разложения по собственным формам колебаний.
Представим искомое решение в виде
X→=Vq→. (2.40)
Здесь V - матрица, составленная из собственных векторов системы уравнений движения V→TK = {X1k, X2k,…,Xnk}:
V =
| X11 |
X12 |
… |
X1n |
| X21 |
X22 |
… |
X2n |
| ... |
... |
... |
... |
| Xn1 |
Xn2 |
… |
Xnn |
(2.41)
q→ - вектор обобщенных (главных) координат:
q→ T(t) = {q1(t), q2(t),...,qn(t)},
37
Напомним, что величины XKi представляют собой амплитудные значения перемещений к-ой массы при колебаниях системы по i-ой собственной (главной) форме и называются амплитудными коэффициентами формы.
qi(t) - функция времени, определяющие закон изменения во времени амплитудных коэффициентов формы. Причем, как известно, собственные векторы обладают свойством обобщенной ортогональности, т.е.
при i≠j
Таким образом, исходя из (2.40), имеем
| Xk= |
Xk1q1(t)+Xk2q2(t)+...+Xknqn(t)= |
i=1∑n |
Xkiqi(t) |
(2.42)
Иллюстрация этого представления приведена на рис. 2.9 для системы с пятью степенями свободы.
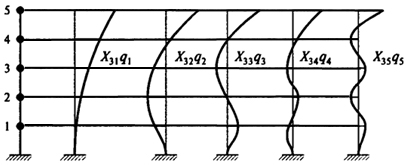
Рис. 2.9. Главные (собственные) формы колебаний системы
с 5-ю степенями свободы
Собственные векторы системы с п степенями свободы определяются из решения алгебраических задач на собственные значения
K →Xi - ωi2M →Xi = 0
(2.43)
если используется система уравнений движения (2.38),
или
LM →Xi - (1/ωi2) →Xi = 0
(2.44)
если используется система уравнений (2.39).
Здесь ωi, - собственные частоты колебаний. В развернутом виде эта система уравнений записывается следующим образом:
| (δ11m1-λi)X1i+ |
δ12m2X2i+ ... + |
δ1nmnXni = 0, |
| δ21m1X1i+ |
(δ22m2-λi)X2i+ ...+ |
δ2nmnXni= 0, |
| ... |
... |
... |
| δn1m1X1i+ |
δn2m2X2i+ ... + |
(δnnmn-λi)Xni= 0, |
(2.45)
где λi= 1/ωi2.
38
Для вывода уравнений, определяющих обобщенные координаты qi, удобнее воспользоваться формой представления уравнений движения в виде (2.38).
Подставляя сюда (2.40) и умножая слева на матрицу VT , получаем
(Ф→ = 0):
VTM V q..→ + VTK Vq→ = - VTM Δ..→
(2.46)
Заметим, что в данном случае задача на собственные значения формулируется в виде
KV-MVΩ2 = 0,(2.47)
где Ω2 - диагональная матрица частот собственных колебаний:
Ω2 =
(2.48)
С учетом ортогональности форм собственных колебаний (2.42) для произведения матриц VTM V можно получить следующее представление
VTM V=Mq(2.49)
где Мq - диагональная матрица обобщенных масс
Мq =
(2.50)
Мi - обобщенные массы, определяемые выражением
(2.51)
Тогда с учетом (2.47) и (2.49), имеем
VtKV = VTM VΩ2 =MqΩ2=Kq (2.52)
Диагональная матрица Kq называется матрицей обобщенной жесткости и легко определяется с помощью формул (2.48) и (2.50)
Kq =
(2.53)
39
Введем представление
VTM Δ..→ = Q→ ,(2.54)
где компоненты вектора Q→определяются выражением
(2.55)
Тогда нетрудно показать, что система уравнений (2.46) распадается на п независимых уравнений, каждое из которых определяет обобщенную координату qi отвечающую i-ой форме колебаний. Действительно, используя введенные представления, записываем (2.46) в виде
Mqq..→ + Kqq→ = - Q→. (2.56)
Учитывая диагональное строение матриц Мq (2.50) и Kq (2.53), имеем
q..i + ωi2qi = - (Qi / Mi)(2.57)
Таким образом, задача построения решения уравнений движения системы с п степенями свободы сводится к решению задачи для линейного осциллятора, описанного выше.
40
