2.5. Определение сейсмических нагрузок для систем
со многими степенями свободы

2.5.1. Дифференциальные уравнения колебаний системы
со многими степенями свободы

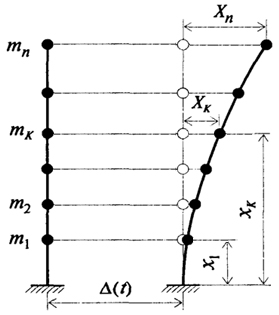
Рис. 2.8. Расчетная схема системы со многими степенями свободы

Для определенности в качестве расчетной схемы системы со многими степенями свободы будем рассматривать консольный стержень с п сосредоточенными массами (рис. 2.8).

Обозначения на этом рисунке приняты в соответствии с обозначениями СНиП II-7-81:

Q_K=m_Kg- вес массы т_к; Х_к - относительное перемещение массы т_к; х_к - расстояние от заделки до этой массы. Используя для расчета этой системы метод перемещений, введем в узлы сосредоточенных масс упругие связи, препятствующие линейным смещениям.

Пусть r_ki,- реакция в K-ой упругой связи, вызванная действием единичного перемещения i-ой связи. Тогда составляя уравнение равновесия всех сил, приложенных к K-ой массе в любой момент времени движения системы, получаем

где Ф_k(t) – силы сопротивления.

Введем вектор перемещений X→^T={X₁,X₂,…,X_n}, вектор сил сопротивления Ф^→T={Ф₁,Ф₂,…,Ф_n}, а также матрицу жесткости

K =

r11	r12	...	r1n
r21	r22	...	r2n
...	...	...	...
rn1	rn2	...	rnn

36

и диагональную матрицу масс

M =

m1
	m2
		...
		…	mn

Тогда систему уравнений (2.37) можно записать в матричной форме

В данном случае уравнения движения системы с п степенями свободы записаны в форме метода перемещений. Для того, чтобы перейти к форме метода сил, вводим матрицу податливости

L =

δ11	δ11	…	δ1n
δ21	δ22	…	δ2n
...	...	...	...
δn1	δn2	…	δnn

причем, как известно, LK = KL = E (единичная матрица).

Умножая уравнение (2.38) слева на матрицу L, получаем

37