Способ угловой засечки применяют для разбивки недоступных точек, находящихся на значительном расстоянии от исходных пунктов.
Различают прямую и обратную угловые засечки.
В способе прямой угловой засечки положение на местности проектной точки С (рис. 16.1) находят отложением на исходных пунктах А и В проектных углов β1 и β2. Базисом засечки служит или специально измеренная сторона, или сторона разбивочной сети. Проектные углы β1 и β2 вычисляют как разность дирекционных углов сторон. Дирекционные углы находят из решения обратной геодезической задачи по проектным координатам определяемой точки и известным координатам исходных пунктов.
На точность разбивки способом прямой угловой засечки оказывают влияние ошибки собственно прямой засечки, исходных данных, центрирования теодолита и визирных целей, фиксации разбивочной точки, т. е.
m2С = m2с.з + m2исх + m2ц + m2ф.(16.5)
Средняя квадратическая ошибка собственно засечки равна
mс.з =
√sin2β1 + sin2β2(16.6)
или
mс.з =
√S12 + S22,(16.7)
где mβ - средняя квадратическая ошибка отложения углов β1 и β2.
Иногда возникает необходимость определить ошибку положения точки по осям координат. В этом случае ошибку засечки вычисляют по формулам
mx2 =
(S12cos2α2 + S22cos2α1);(16.8)
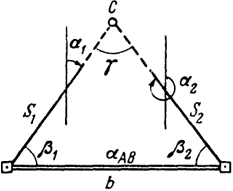
Рис. 16.1. Схема разбивки способами прямой угловой и линейной засечек
205
my2 =
(S12sin2α2 + S22cos2α1).(16.9)
Для приближенных расчетов принимают S1 = S2 = S. Тогда формула (16.7) будет иметь вид
mс.з =
S.(16.10)
При заданной ошибке тβ величина ошибки засечки будет зависеть от угла γ и расстояния S до определяемой точки. С учетом влияния угла γ и расстояния S ошибка засечки будет минимальной при γ = 109°28’.
Ошибка исходных данных является следствием ошибок в положении пунктов А и В. Если принять, что тА = тB = тАВ, то
m2исх = m2AB
.(16.11)
Для приближенных расчетов, приняв S1 = S2 = S и γ = 90°, можно записать
mисх =
S.(16.12)
По аналогии с формулами (16.11) и (16.12) совместное влияние ошибок центрирования теодолита и визирной цели выразится формулами
mц2 = e2
= e2
;(16.13)
mц =
S,(16.14)
где l - величина линейного элемента центрирования.
При разбивочных работах центрирование теодолита и визирных целей с помощью оптических отвесов, фиксация выносимой точки могут быть выполнены сравнительно точно. Поэтому основными ошибками, определяющими точность способа прямой угловой засечки, являются ошибки собственно засечки и исходных данных. Суммарная величина этих ошибок составит
m2C = (
+ m2AB) (16.15)
206
или
m2C = (
+
)(S12 + S22).(16.16)
При S1 = S2 = S, γ = 90° ошибка в положении выносимой в натуру точки выразится приближенной формулой
тC = √(
)2b2 + m2AB.(16.17)
Часто при проектировании разбивочных работ решают вопрос о необходимой точности отложения разбивочных элементов, если задана точность определения проектного положения выносимой в натуру точки. Для прямой угловой засечки определяют ошибку отложения проектных углов.
Так, например, для b = 500 м, mC = 20 мм, тАВ = 8 мм, используя формулу (55), будем иметь
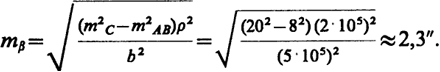
Отложить с такой точностью угол довольно сложно. Требуемая точность разбивки в этом случае может быть достигнута следующим образом. Отложив с возможной точностью углы β1 и β2, определяют в натуре положение точки С. Затем на опорных пунктах соответствующим числом приемов измеряют точное значение отложенных углов. Для приведенного примера при использовании теодолита 2Т2 надо выполнить не менее четырех приемов. Измеряют также угол γ на точке С. Распределив невязку в треугольнике поровну на все три угла, определяют координаты точки С. Сравнивая их с проектными значениями, находят поправки (редукции), по которым в натуре смещают (редуцируют) приближенно вынесенную точку С. Такой способ называют способом замкнутого треугольника.
На принципе редуцирования основано и применение для разбивки способа обратной угловой засечки. На местности находят приближенно положение О’ разбиваемой проектной точки О (рис. 16.2). В этой точке устанавливают теодолит и с требуемой точностью измеряют углы не менее чем на три исходных пункта с известными координатами. По формулам обратной засечки вычисляют координаты приближенно определенной точки и сравнивают их с проектными значениями. По разности координат вычисляют величины редукции (угловой и линейный элементы) и смещают точку в проектное положение. Для контроля на этой точке измеряют углы,
207
вновь вычисляют ее координаты и сравнивают их с проектными. В случае недопустимых расхождений все действия повторяют.
Для вычисления координат точки О’ можно использовать формулы Деламбера и Гаусса. Применительно к (рис. 16.2), они будут иметь вид:
tgαAJ’ =
| (YC - YA)ctgβ1 + (YB - YA)ctgβ2 - (XB - XC) |
| (XC - XA)ctgβ1 + (XB - XA)ctgβ2 - (YB - YC) |
;(16.18)
Xo’ =
| XBtgαBO’ - XAtgαAO’ + (YA - YB) |
| tgαBO’ - tgαAO’ |
Y = YB + (Xo’ - XB)tgαBO’;
Y = YC + (Xo’ - XC)tgαCO’;
αBO’ = αO’A + β2 ± 180°; αCO’ = αO’A - β1 ± 180°.(16.19)
На точность разбивки способом обратной угловой засечки оказывают влияние ошибки собственно засечки, исходных данных, центрирования теодолита и визирных целей, фиксации разбивочной точки и редуцирования. Очевидно, что при сравнительно больших расстояниях от определяемого до опорных пунктов влияние первых двух источников будет наиболее существенным; остальными ошибками можно пренебречь.
Ошибка собственно обратной засечки может быть подсчитана по приближенной формуле
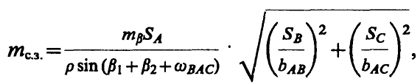(16.20)
где S - расстояние от определяемого до соответствующих опорных пунктов; b - расстояние между соответствующими опорными пунктами; ωВАС - угол между исходными сторонами.
Если для приближенных расчетов принять SA = SB = SC = Scp;bAB = bAC = bср, то формула (16.10) примет вид
(16.21)
Ошибки исходных данных учитывают по формуле
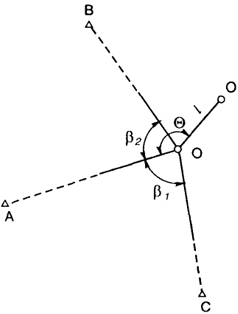
Рис. 16.2.
Схема способа обратной угловой засечки№
208
(16.22)
где тА = тB = тс = тАВс - ошибка в положении исходного пункта; τ = β1 + β2 + ωABC - 180°
Для приближенных расчетов
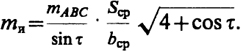(16.23)
В качестве примера соответственно по формулам (16.21) и (16.23) рассчитаем точность определения положения точки О’ при Sср ≈ 1350 м, bср ≈ 2200 м, ωBAC ≈ 80°, mβ = 2’’, тABC = 5 мм.
Получим mс.з. = 11,5 мм, mи = 6,2 мм, а общая ошибка
mO' = √mс.з.2 + mи2 = 13,1 мм(16.23)
209
