Разбивочные работы по существу сводятся к фиксации на местности точек, определяющих проектную геометрию сооружения. Плановое положение этих точек может быть определено с помощью построения на местности проектного угла от исходной стороны и отложения проектного расстояния от исходного пункта.
При построении проектного угла одна точка (вершина угла) и исходное направление обычно бывают заданы. Необходимо на местности отыскать второе направление, которое образовывало бы с исходным проектный угол β (рис. 15.2). В нашем случае ВА - исходное направление, В - вершина проектируемого угла.
Работы ведут в следующем порядке. Устанавливают теодолит в точку В. Наводят зрительную трубу на точку А и берут отсчет по лимбу. Далее прибавляют к этому отсчету проектный угол β и, открепив алидаду, устанавливают вычисленный отсчет. Теперь визирная ось зрительной трубы теодолита указывает второе искомое направление. Это направление на соответствующем проекту расстоянии фиксируют на местности в точке С1. Аналогичные действия выполняют при другом круге теодолита и отмечают на местности вторую точку С2. Из положения двух точек берут среднее (точка С, рис. 15.2), принимая угол ABC за проектный.
196
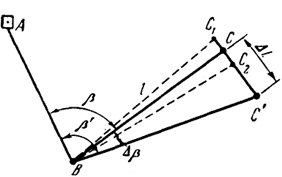
Рис. 15.2. Схема построения в натуре проектного угла
Стандартные геодезические приборы, изготовленные серийно, по точности предназначены для выполнения измерений, а не построений. В результате точность отложения разбивочных элементов этими приборами оказывается ниже, чем точность измерений с использованием этих приборов. Поэтому, если необходимо построить проектный угол с повышенной точностью, то поступают следующим образом.
Построенный в натуре угол измеряют несколькими приемами и определяют его более точное значение β’. Число приемов п измерения угла можно определить по приближенной формуле
n =
,(15.4)
где т’β - номинальная для данного теодолита средняя квадратическая ошибка измеренного угла; тβ - требуемая средняя квадратическая ошибка отложения угла.
Например, для того, чтобы отложить угол со средней квадратической ошибкой 2’’ теодолитом 2Т5, надо его измерить числом приемов, равным
n =
= 6.
Измерив построенный в натуре угол, вычисляют поправку
∆β = β’ - β,(15.5)
которую необходимо ввести для уточнения построенного угла. Зная проектное расстояние ВС = l, вычисляют линейную поправку СС’ = ∆l. Из геометрии построений (см. рис. 15.2) следует, что
∆l = l
,(15.6)
где β и ρ выражены в секундах.
Далее откладывают от точки С перпендикулярно к линии ВС величину вычисленной поправки ∆l и фиксируют точку С’. Угол ABC’ и будет равен проектному углу с заданной точностью. Для контроля угол ABC' измеряют. Если полученное значение отличается от проектного на допускаемую величину, то работу заканчивают. В противном случае требуется дальнейшее уточнение.
197
Точность построения на местности проектного угла зависит от инструментальных ошибок, ошибок собственно измерения (визирования и отсчета по лимбу), а также ошибок из-за влияния, внешних условий. Ошибки центрирования, редукции и исходных данных (ошибки в положении пунктов А и В) на точность отложения проектного угла влияния не оказывают, что позволяет учитывать их отдельно. В этом заключается еще одна особенность разбивочных работ. Однако эти ошибки вызывают смещение на местности направления ВС и выносимой точки С.
Необходимая точность отложения линейной поправки (редукции) ∆l может быть подсчитана по формуле
m∆l = l
.(15.7)
Если l = 200 м, m∆β = 2’’, то получим т = 2 мм. Очевидно, что с такой точностью линейную редукцию можно легко отложить при помощи рулетки или линейки с миллиметровыми делениями.
Для построения проектной длины линии необходимо от исходной точки отложить в заданном направлении расстояние, горизонтальное приложение которого равно проектному значению. Надо помнить, что в проекте задается именно горизонтальное проложение. Поправки в линию за компарирование, температуру и наклон
Таблица 15.2

местности необходимо вводить непосредственно в процессе ее построения. Но это затрудняет работу, особенно при необходимости вынесения линии с высокой точностью. Поэтому часто поступают таким же образом, как и при построении углов, т. е. используют способ редукции. На местности от исходной точки А (рис. 15.3) сначала откладывают и закрепляют приближенное значение проектного расстояния (точка В’. Это расстояние с необходимой точностью измеряют компарированными мерными приборами или точными дальномерами, учитывая все поправки. Вычислив длину закрепленного отрезка, сравнивают его с проектным значением, находят линейную поправку
198
∆l = lnp - lизм(15.8)
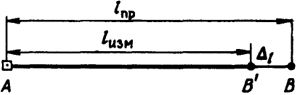
Рис. 15.3. Схема отложения проектной длины линии
и откладывают ее с соответствующим знаком от конечной точки В’ отрезка. Затем, для контроля, построенную линию АВ измеряют.
Точность построения проектного расстояния lпр в способе редукции в основном зависит от точности линейных измерений расстояния АВ’. Исходя из требуемой точности определения проектного расстояния, выбирают приборы для измерений.
Если проектное расстояние откладывается непосредственно в натуре, то поправки за компарирование, температуру и наклон местности вводят со знаками, обратными тем, которые учитывают при измерении линий (табл. 15.2).
Поправки линейных измерений при применении проволок и мерных лент. Уравнение мерного прибора можно записать в общем виде
lt = lн + ∆lк + αlt0(t - t0) + βlt0(t2 - t02),(15.9)
где lt - длина мерного прибора при температуре измерения t - номинальная длина прибора; lн - длина мерного прибора при температуре t0, полученная из компарирования; ∆lк - поправка за компарирование; α, β - коэффициенты линейного расширения.
Пусть, например, при выносе в натуру проектной линии использовался мерный прибор, длина которого при температуре измерения была меньше его номинальной длины. В этом случае отложенная линия будет короче проектной, и, следовательно, поправку надо вводить со знаком "плюс". Если этот прибор использовать для измерения линии, то поправку надо вводить со знаком "минус", так как при измерении укороченным мерным прибором результат получится большим, чем следует.
Если же мерный прибор при температуре измерения имеет длину, большую номинальной, то при измерении линии поправка будет иметь знак "плюс", при отложении - "минус".
При измерении линии на наклонной местности поправка за наклон для приведения ее длины к горизонту вводится со знаком "минус", так как наклонное расстояние всегда больше горизонтального проложения.
При отложении линий все размеры в проекте приведены к горизонту. Поэтому при отложении проектного размера на наклонной местности он укорачивается. Значит поправку необходимо вводить со знаком "плюс".
В зависимости от требуемой точности для отложения проектных расстояний используют стальные и инварные мерные приборы, оптические дальномеры, светодальномеры.
199
