Под невозмущенным (кеплеровым) движением спутника понимают его движение под воздействием только силы притяжения Земли. В соответствии со вторым законом Ньютона движение центра масс спутника в инерциальной системе координат X0Y0Z0 описывается уравнением:
F = mg,
где F - вектор силы притяжения Земли, т - масса спутника, g - вектор центростремительного ускорения, или
F = k
=
,
171

Рис. 14.10. Ориентация орбитальной плоскости
где k = 6,672·10-11 м3/кгс2 - универсальная гравитационная постоянная; М = 5,974242·1024 кг - масса Земли; r - расстояние от центра Земли до спутника; μ = kM = 3,9860044 м3/с2 - геоцентрическая гравитационная постоянная Земли.
В соответствии с первым законом Кеплера, любая траектория спутника, движущегося в поле тяготения Земли, лежит в неподвижной плоскости, так называемой орбитальной плоскости, проходящей через центр тяготения, и представляет собой кривую второю порядка, в одном из фокусов которой находится центр притяжения.
Ориентацию орбитальной плоскости характеризуют ее положением относительно экваториальной плоскости XOY (рис. 14.10). Линию пересечения этих плоскостей называют линией узлов. Узлами орбиты спутника являются точки пересечения орбиты с экваториальной плоскостью. Узел U, соответствующий движению спутника из южной небесной полусферы в северную называют восходящим, а узел D, соответствующий движению из северной небесной полусферы в южную - нисходящим.
Положение плоскости орбиты спутника относительно экваториальной плоскости определяют два орбитальных элемента - долгота восходящего узла Ω и наклонение орбиты i. Угол Ω отсчитывается в экваториальной плоскости от оси X до линии узлов и может изменяться в пределах от 0° до 180°. При = 90° орбита называется полярной, при i = 0° - экваториальной, в остальных случаях - наклонной.
Уравнение орбиты спутника в орбитальной плоскости в полярной
172
системе координат (r0, υ) с центром, совпадающим с центром Земли, имеет вид:
r =
,
где Р - фокальный параметр, е - эксцентриситет, υ0 - угол между положительным направлением полярной оси и фокальной осью.
На рис. 14.11 приведена эллиптическая орбита спутника. В одном из фокусов эллипса находится Земля. Прямую линию, проходящую через фокусы эллипса, называют линией апсид. Точки пересечения этой линии с эллипсом называют апсидами. Точку, ближайшую к Земле, называют перицентром или перигеем (П), а удаленную - апоцентром или апогеем (А). Ориентация орбиты в орбитальной плоскости характеризуется углом перигея (аргументом) н>п между направлением на перигей и линией узлов.
Размеры орбиты спутников характеризуются следующими параметрами:
большая полуось эллипса:
a =
линейный эксцентриситет:
d = a·e
Если спутник движется строго в соответствии с законами Кеплера (при отсутствии возмущающих воздействий), то пять параметров орбиты Ω, i, wп, р, постоянны и не меняются при движении спутника, а шестой параметр υ (истинная аномалия) характеризует положение спутника на орбите в каждый фиксированный момент времени tk. Время tk, характеризующее нахождение спутника в конкретной
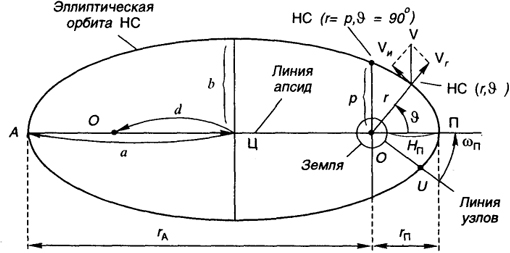
Рис. 14.11. Эллиптическая орбита спутника
173
точке орбиты, называется эпохой. Время нахождения спутника в какой-либо характерной точке орбиты имеет собственное название, например, время перигея tп.
В связи с тем, что генераторы частоты, установленные на каждом спутнике, имеют некоторые погрешности, то показания часов на спутнике отличается от времени GPS. С целью приведения времени спутника в систему времени GPS необходимо вычислить и ввести поправку в часы спутника, используя полиномиальные коэффициенты, которые передаются в спутниковом сообщении. Время спутника исправляют на величину ∆ts:
t = ts -∆ts
где ∆ts = a0 + a1(t - toc) + a2(t - toc)2.
Вычисляют промежуток времени от опорной эпохи до момента данного измерения:
tk = t - toc.
В дальнейших расчетах потребуются следующие константы:
- ωe = 7,2921151467·10-5 рад/с - угловая инерциальная скорость вращения Земли;
- μ = 3986005·108 м3/с2 - гравитационный параметр Земли;
- π = 3,1415926535898 - точное значение числа π.
Среднее движение на момент t^ вычисляется по формуле:
n0 =
а скорректированное среднее движение равно:
n = n0 + ∆n.
Средняя аномалия вычисляется по формуле:
Mk = M0 + ntk,
а эксцентрическую аномалию на момент излучения сигнала находят, используя уравнение Кеплера:
Ek = Mk + esinEk.
Эта задача решается итерациями, воспользовавшись тем, что эксцентриситет орбит спутника мал (е ≤ 0,001), в первом приближении принимают:
E1 = M1
174
а затем уточняют по формуле:
Ei = M + esinEi-1, i = l, 2, 3...
затем вычисляют истинную аномалию по формулам:
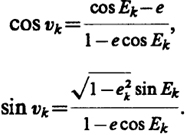
Приближение к аргументу широты равно:
υ0k = υk + ω
В связи с тем, что спутник движется по возмущенной орбите, в связи с неравномерным распределением масс в теле Земли, солнечным давлением Солнца на спутник и др., в навигационном сообщении спутника, кроме шести параметров Кеплера, содержится 9 корректирующих поправок.
Корректирующую поправку к аргументу широты вычисляют по формуле:
δU0k = Cuсcos2U0k + Cussin2U0k.
Аргумент широты на момент излучения равен:
Uk = U0k + δUk.
Корректирующую поправку к радиус-вектору вычисляют по формуле:
δrk = Crscos2U0k + Crssin2U0k.
Радиус-вектор на момент tk вычисляют по формуле:
rk = A(1 - ecosEk) + δrk.
Найденные величины rk и Ek позволяют вычислить координаты спутника в плоскости оскулирующей орбиты:
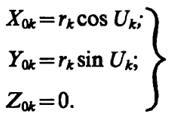
Коррекцию за наклон орбиты к плоскости экватора вычисляют по формуле:
175
δik = Ciccos2U0k + Cissin2U0k,
а наклон орбиты к плоскости экватора равен:
Долготу узла на момент tk вычисляют по формуле:
λk = Ω0 + (Ω - ωe)tk - ωet0c.
Координаты спутника в системе координат WGS-84 могут быть получены по следующим формулам:
Xk = X0kcos λk - Yoksin λkcosik;
Yk = X0ksin λk - Yokcos λkcosik
Zk = sin ik.
Под эфемеридами спутников понимают прогнозируемые координаты положения спутников на момент времени, интересующий потребителя. Применительно к спутниковым навигационным системам эфемериды спутников состоят из двух частей:
- - математической модели движения спутников, которая опубликована в научной литературе;
- - параметров математической модели, которые передаются в навигационном сообщении спутника.
Поскольку описать с высокой точностью реальное движение спутников не удается даже при наличии столь значительного количества коэффициентов, то прогнозируемую орбиту спутника разбивают на интервалы длительностью 1 ч. Каждый час в навигационном сообщении обновляются все параметры и корректирующие коэффициенты.
176
