Широкое внедрение в практику геодезических работ светодальномерной техники привело к распространению линейно-угловых построений. В линейно-угловых сетях измеряются все или часть углов и сторон. По сравнению с триангуляцией и трилатерацией сеть, в которой удачно сочетаются угловые и линейные измерения, в меньшей степени зависит от геометрии фигуры; существенно уменьшается зависимость между продольным и поперечным сдвигами; обеспечивается жесткий контроль угловых и линейных измерений. Линейно-угловая сеть позволяет вычислить координаты пунктов точнее, чем в сетях триангуляции и трилатерации, примерно в 1,5 раза.
При уравнивании линейно-угловых сетей возникает вопрос о соотношении ошибок угловых и линейных измерений. Это соотношение считается приемлемым при выполнении следующего условия
= .(13.20)
На практике стремятся это соотношение выдержать в пределах
>
∙ < 3,(13.21)
так как при
=
≤
линейные измерения практически не повышают точность элементов сети; при
=
≥ 3 влияние угловых измерений на повышение точности элементов сети незначительно. В качестве примера повышения точности в линейно-угловых сетях можно привести формулы вычисления ошибок уравненных длин сторон и углов треугольника при измерении всех его элементов:
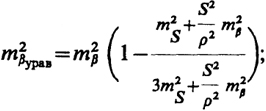(13.22)
151
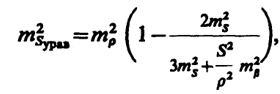(13.23)
где ms и тβ - средние квадратические ошибки измерения длин линий и углов; S - длина стороны равностороннего треугольника.
Значительное повышение точности в линейно-угловых сетях возникает при определении ошибок координат пунктов.
При уравнивании линейно-угловых сетей важно правильно установить соотношение весов измеренных углов и длин сторон. Веса измеренных длин сторон и углов обычно вычисляют по формулам
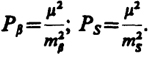(13.24)
Для удобства вычислений обычно принимают μ2 = m
и при уравнивании по углам получают
.
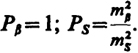При вычислении весом следует помнить, что размерности тβ и ms должны соответствовать размерности вычисляемой невязки. Например, если невязки вычисляются в угловых секундах и сантиметрах, то эти размерности должны использоваться и при вычислении весов.
Оригинальным линейно-угловым построением, применяемым лишь в инженерно-геодезической практике, является четырехугольник без диагоналей (рис. 13.4), в котором измерены две смежные стороны, например а и б, и все углы. В бездиагональном четырехугольнике стороны с и d вычисляют по формулам
с =
;
d = .(13.25)
Если измерены две несмежные стороны, например b и d то в этом случае стороны а и с могут быть вычислены по формулам
a =
;
c = .(13.26)
152
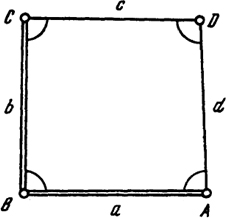
Рис. 13.4. Схема четырехугольника без диагоналей
В сложных сетях, составленных из бездиагональных четырехугольников, нет необходимости измерять две стороны в каждом четырехугольнике. Они могут быть получены из решения предыдущих фигур.
При равноточных угловых измерениях средние квадратические ошибки вычисления длины стороны для прямоугольного четырехугольника равны
(13.27)
Бездиагональные четырехугольники применяются в основном для создания строительных сеток.
Другим примером линейно-угловой сети служит опорная сеть, применяемая при строительстве мостовых переходов. В таких сетях измеряют все четыре стороны и четыре угла; в связи с этим такие сети иногда рассматриваются как своеобразный замкнутый полигонометрический ход, в котором измерены два левых и два правых угла.
153
