Метод трилатерации применяют для построения инженерно-геодезических сетей 3 и 4 классов, а также сетей сгущения 1 и 2 разрядов различного назначения. Приведем наиболее распространенные требования к сетям (табл. 4).
Сети трилатерации, создаваемые для решения инженерно-геодезических задач, часто строят в виде свободных сетей, состоящих из отдельных типовых фигур: геодезических четырехугольников, центральных систем или их комбинаций с треугольниками.
Типовой фигурой трилатерации является треугольник с измеренными сторонами а, b и с (рис. 13.2).
Таблица 13.4
| Основные показатели |
4 класс |
1 разряд |
2 разряд |
| Длина стороны, км |
1 - 5 |
0,5 - 6 |
0,25 - 3 |
| Предельная относительная ошибка определения длин сторон |
1:50000 |
1:20000 |
1:10000 |
| Минимальный угол в треугольнике, угл. градус |
20 |
20 |
20 |
| Минимальный угол в четырехугольнике, угл. градус |
25 |
25 |
25 |
| Число треугольников между исходными пунктами |
6 |
8 |
10 |
148

Рис. 13.2. Счема треугольника трилатерация
Углы в треугольнике трилатерации вычисляют по одной из следующих формул:
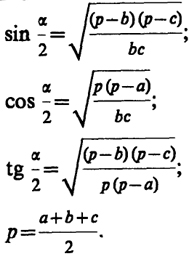 (13.15)
(13.15)
Средняя квадратическая ошибка вычисленного угла может быть определена по формуле
m
= ρ2(Am
+ B2m
+ C2m
),(13.16)
где тa, тb и тc - средние квадратические ошибки измерения сторон;

где ha - высота треугольника, опущенная из вершины на сторону а.
Для линейно протяженных объектов сеть трилатерации создают из цепочки треугольников (рис. 13.3, а). Одним из основных недостатков вытянутого ряда цепочки треугольников с измеренными сторонами является то, что в таких сетях поперечный сдвиг ряда ти существенно превышает продольный mt.
При оценке ожидаемой точности ряда равносторонних треугольников трилатерации используют формулы:
а) для продольного сдвига
mt = ms√
(при N четном);(13.17)
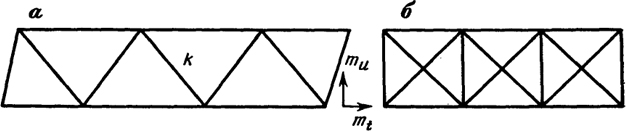
Рис. 13.3. Схемы сети трилатерации из цепочки треугольников
149
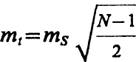
(при
N нечетном),
где ms - средняя квадратическая ошибка измерения сторон; N - число фигур ряда;
б) для поперечного сдвига
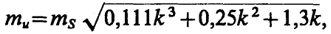 (13.18)
(13.18)
где k - порядковый номер связующей стороны;
в) для дирекционного угла связующей стороны
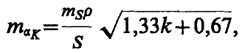
где S - длина сторон треугольников.
Еще одним недостатком трилатерационных сетей из треугольников является отсутствие полевого контроля качества измерений для каждой фигуры, так как сумма вычисленных углов треугольника всегда равна 180° при любых ошибках измерений длин сторон, даже при грубых промахах. В связи с этим на практике часто используют сети из геодезических четырехугольников (рис. 13.3, б).
В каждом геодезическом четырехугольнике измерено шесть сторон, причем одна из них (любая) является избыточной и может быть вычислена, используя результаты измерений других сторон. Это может служить полевым контролем качества измерений длин линий. Кроме того, геодезический четырехугольник является более жесткой фигурой и ряд, составленный из таких фигур, обладает более высокой точностью.
Оценка точности ряда геодезических четырехугольников, состоящего из квадратов и уравненного за условия фигур, может быть выполнена по следующим формулам:
mt = ms√0,9N;
mu = ms√0,67N3 - 0,13N2 + 0,98N + 1,4;
mαk =
√2N.(13.19)
Широкое распространение в практике инженерно-геодезических работ сети трилатерации получили при строительстве высокоэтажных зданий, дымовых труб, градирен, атомных электростанций, а также при монтаже сложного технологического оборудования. В таких сетях высокую точность измерения длин сторон (до десятых долей миллиметра) обеспечивают, используя высокоточные светодальномеры, инварные проволоки, а в некоторых случаях и жезлы
150
специальной конструкции. Сети трилатерации с короткими сторонами принято называть сетями микротрилатерации. Иногда сети микротрилатерации являются единственно возможным методом создания геодезического обоснования для производства разбивочных работ.
151
