Триангуляционные сети в инженерно-геодезических работах используются в качестве основы для топографических съемок и разбивочных работ, а также для наблюдений за деформациями сооружений.
Для съемочных работ триангуляционная сеть позволяет сократить длины развиваемых на ее основе сетей сгущения и способствует уменьшению ошибок в сетях низших разрядов и съемочных сетях. Выбор класса сети для этой цели определяется в основном
144
площадью съемки. Так, для крупнейших городов применяется триангуляция до 2 класса включительно. В большинстве случаев исходным обоснованием для съемочных работ служит триангуляция 4 класса. Триангуляция используется и для построения сетей сгущения 1 и 2 разрядов.
Приведем основные характеристики триангуляции для инженерно-геодезических работ широкого назначения (табл. 13.1).
Для разбивочных работ триангуляция может служить непосредственной основой, с пунктов которой производится разбивка сооружений, или опорой для развития сетей низших разрядов, в свою очередь используемых для разбивки. Примером может служить триангуляция для строительства гидротехнических сооружений, тоннелей, мостов.
Таблица 13.1
Таблица 13.2
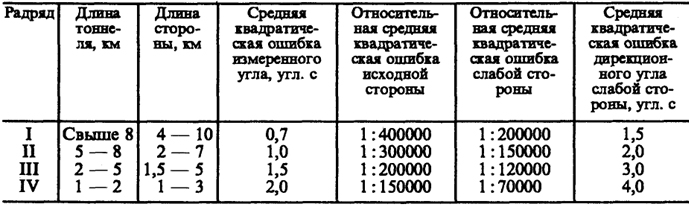
Таблица 13.3
Приведем основные характеристики тоннельной (табл. 13.2) и гидротехнической (табл. 13.3) триангуляции.
145
Из приведенных таблиц следует, что характеристики специальных триангуляции отличаются от государственных в основном длинами сторон, причем в сторону уменьшения. Это обстоятельство неизбежно приводит к повышению требований к отдельным измерительным операциям, таким как центрирование теодолита и визирных целей при угловых измерениях и т. п.
Особенностью разбивочной триангуляции является необходимость соблюдения точностных требований во взаимном положении смежных пунктов или пунктов, разделенных двумя-тремя сторонами. Это требование обусловлено тем, что с пунктов сети требуется вынести в натуру систему точек, как правило, принадлежащих единому сооружению или единому комплексу сооружений, связанных конструктивно или технологически.
Триангуляционные сети, предназначенные для наблюдений за плановыми смещениями сооружений, чаще всего применяются на крупных гидротехнических объектах. В основном они используются для измерения смещений недоступных точек и для контроля устойчивости исходных опорных пунктов других построений. Характерной особенностью триангуляционных сетей для этого вида работ являются высокие требования к точности определения координат пунктов (2 - 5 мм) при небольших длинах сторон.
При развитии инженерно-геодезических сетей методом триангуляции наиболее типичными построениями являются (рис. 13.1): цепи треугольников (для линейно протяженных объектов), центральные системы (для городских и промышленных территорий), геодезические четырехугольники (для мостовых и гидротехнических сооружений), вставки пунктов в треугольники и небольшие сети из этих фигур. Возможны и комбинированные построения.
В сетях триангуляции треугольники стараются проектировать близкими к равносторонним; в особых случаях острые углы допускают
Рис. 13.1. Инженерно-геодезические сети триангуляции
146
до 20°, а тупые - до 140°. В свободных сетях для контроля масштаба сети необходимо иметь не менее двух непосредственно измеренных базисных сторон.
Уравнивание результатов измерений выполняют строгими способами.
При разработке проектов триангуляционных сетей расчет ожидаемой точности производят, как правило на ЭВМ, используя различные программы.
Для предварительной оценки ожидаемой точности некоторых, применяемых в инженерной практике, схем и построений можно пользоваться приближенными формулами.
Так, продольный сдвиг ряда, состоящий из приближенно равносторонних треугольников, при уравнивании его за условие фигур по направлениям вычисляется по формуле
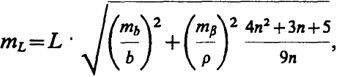(13.8)
где п - число промежуточных сторон в диагонали ряда L; (
) - относительная средняя квадратическая ошибка измерения
базисной стороны; тβ - средняя квадратическая ошибка измеренного угла; знак плюс перед 3 п берется при четном числе треугольников в ряде, знак минус - при нечетном.
Поперечный сдвиг такого же ряда и при тех же условиях вычисляется по формулам:
при четном числе треугольником в ряде
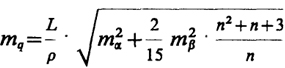(13.9)
при нечетном числе треугольников в ряде
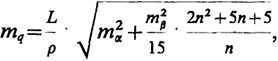(13.10)
где тα - средняя квадратическая ошибка дирекционного угла исходной стороны.
Средняя квадратическая относительная ошибка длины связующей стороны треугольника с номером К вычисляется по формуле
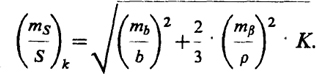(13.11)
147
То же для дирекционного угла по формуле
(13.12)
Для треугольников произвольной формы со связующими углами А и В
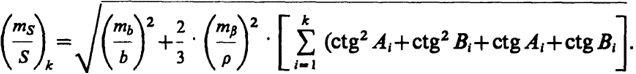(13.13)
Если расчет для промежуточной стороны ряда ведется от двух исходных базисов, то среднее весовое из двух ошибок, полученных по формуле (13.13) может быть подсчитано по формуле
(13.14)
148
