13.2. ПРИНЦИПЫ ПРОЕКТИРОВАНИЯ И РАСЧЕТ ТОЧНОСТИ
ПОСТРОЕНИЯ ОПОРНЫХ СЕТЕЙ

При проектировании инженерно-геодезических сетей, исходя из назначения работ, вида и площади объекта, необходимо решить следующие основные задачи:

• выяснить исходные требования к точности построения сети;
• определить количество ступеней развития сети;
• выбрать для каждой ступени вид построения сети;
• назначить общие требования к точности построения сети на каждой ступени;

140

• найти требуемую точность отдельных видов измерений на каждой ступени построения сети.

Эти задачи могут быть решены двумя путями.

Первый путь. Исходя из условии проектирования, определяют конкретный вид сети и выбирают класс ее построения. Для выбранного класса сети существуют геометрические и точностные параметры, определяемые нормативными документами. Руководствуясь ими, разрабатывают проект и выполняют его оценку. Результаты оценки по каким-либо конечным параметрам сравниваются с заданными или нормативными и делаются соответствующие выводы. Далее выбираются рекомендованные инструкциями методы и средства измерений. Такой принцип решения обычно применяют при проектировании опорных сетей для производства крупномасштабных топографических съемок и выноса в натуру основных осей зданий и сооружений при строительстве населенных пунктов.

Второй путь. Для опорных сетей специального назначения проектирование и расчет точности ведутся, руководствуясь назначением сети; задаются или рассчитываются исходные точностные требования. Исходя из необходимой плотности и возможных мест расположения пунктов, проектируется схема построения сети. При этом можно руководствоваться геометрическими параметрами, приблизительно соответствующими определенному классу. Далее на основе расчетов определяется действительный класс построений для каждой ступени развития сети. Так же на основе расчетов определяется методика и выбираются средства измерений на каждой ступени.

Основу расчетов для обоих случаев проектирования составляет решение известного точностного уравнения

m_F = μ√

1

PF

 (13.1)

где т_f - ошибка функции наиболее слабо определяемого или требуемого элемента в уравненной сети; μ - ошибка единицы веса измерений; 1/P_F = Q_F - обратный вес оцениваемого элемента.

В первом случае, найдя обратный вес и задавая ошибку единицы веса, соответствующую какому-либо нормативному классу, определяют ошибку m_f функции оцениваемого элемента сети и сравнивают ее с нормативной. Во втором - по вычисленной величине обратного веса и заданной ошибке функции оцениваемого элемента находят ошибку единицы веса μ. На основе полученной величины μ выбирают методику измерений.

Таким образом, во всех случаях расчета точности сети необходимо определить обратный вес и ошибку функции оцениваемого элемента.

При строгом решении обратный вес функции оцениваемого элемента обычно находят из уравнения. Так как измерения пока не

141

проводились, вопрос об уравнивании отпадает. Но, поскольку оценивается обратный вес функции уравненных элементов, то для его вычисления, принимая свободные члены соответствующих уравнений равными нулю, можно использовать принципы и приемы уравнивания.

Например, при применении коррелатного способа составляют условные уравнения, присоединяют к ним уравнение оцениваемой функции, переходят к нормальным уравнениям и из их решения находят обратный вес.

Основу любого геодезического проектирования составляют требования к точности выполнения работ. Применительно к построению опорных инженерно-геодезических сетей задача состоит в назначении или расчете ошибки функции того или иного элемента сети. Поскольку опорные сети могут развиваться в несколько этапов, то существуют понятия об исходной и поэтапной точностях. Под исходной точностью понимают точность определения положения съемочной точки, осадок реперов и т. п. Поэтапная точность является функцией от исходной, ее долей, приходящейся на каждый этап построения. При одностадийном построении исходная точность и поэтапная совпадают.

В практике инженерно-геодезических работ существуют различные пути решения задачи по определению исходной и поэтапной точностей.

Исходная точность может быть задана в техническом задании, в нормативных документах или получена расчетным путем.

Так, например, при расчете точности планового обоснования для съемочных работ в качестве исходной принимают среднюю квадратическую ошибку планового положения съемочной точки. Рассчитывают ее по формуле

m_исх = 0,2 мм·М,(13.2)

где М - знаменатель масштаба съемки.

При расчете точности высотного обоснования для съемочных работ в качестве исходной может быть принята ошибка в определении отметки точки по горизонталям. Ее определяют по формуле

m_Hисх =

1

5

 h(13.3)

где h - высота сечения рельефа.

Для определения поэтапной точности наиболее распространенным является следующий путь.

Пусть опорная сеть проектируется в n ступеней. Общая (исходная) ошибка будет складываться из суммарных случайных ошибок m₁, m₂, ..., т_n построения для каждой ступени. Если ошибки слабо зависимы, то можно написать

m

2

исх

  = m

2

1

  + m

2

2

  + … + m

2

n

.(13.4)

142

Исходя из практической необходимости, для решения уравнения (13.4) ставится условие, чтобы для каждой последующей ступени построения сети ошибки предыдущей можно было считать пренебрегаемой малыми. Это возможно, если ошибки каждой предыдущей ступени будут в К раз меньше ошибок последующей, т. е.

m₁ =

m2

K

  ; m₂ =

m3

K

 

и т. д.

Коэффициент К называют коэффициентом обеспечения точности, показывающим, во сколько раз ошибка исходных данных должна быть меньше ошибки измерений, чтобы первой можно было пренебречь. Для массовых геодезических работ, в том числе и для опорных сетей, К принимают равным двум и одинаковым для всех ступеней построения обоснования.

В качестве примера рассмотрим схему построения обоснования для съемки масштаба 1:500, состоящую из трех ступеней. Для этого случая

m

2

общ

  = m

2

1

  + m

2

2

  + m

2

3

  .(13.5)

Исходную ошибку найдем по формуле (13.2)

m_общ = 0,2 мм·500 = 10 см.

Выразив ошибки т₂ и т₃ через ошибку т₁ будем иметь

m₂ = Km₁; m₃ = Km₂ = K²m₁(13.6)

Подставляя выражения (13.6) в формулу (13.5) и принимая К = 2, получим

т

2

общ

  = т

2

1

  + 4т

2

1

  + 16т

2

1

  = 21m

2

1

 ,

откуда

m₁ =

10см

√21

  10 см = 2,2 см; т₂ = 4,4 см; m₃ = 8,8 см.

Полученные величины представляют собой ошибки пунктов в самом слабом месте схемы построения сети для каждой ступени по отношению к пунктам, на которые эта ступень опирается. Например, можно считать, что m₃ - это ошибка в середине теодолитного хода, опирающегося на пункты ходов полигонометрии соответствующего разряда; т₂ - ошибка в середине полигонометрического хода, опирающегося на пункты триангуляции соответствующего класса, a m₁ - ошибка в слабом месте сети триангуляции по отношению к ее исходному пункту или взаимного положения двух смежных пунктов триангуляции.

143

Следует отметить, что совместное переуравнивание всей опорной сети в целом, которое производят после ее полного завершения, позволяет получить более однородную по точности сеть. Это обстоятельство является важным при последующих разбивочных работах.

Для определения необходимой точности измерений на каждой ступени развития обоснования определяют зависимость между ошибкой этих измерений и ошибкой, полученной для данной ступени из общих расчетов.

Так, например, для вытянутого хода светодальномерной полигонометрии средняя квадратическая ошибка М в положении конечной точки хода выражается формулой

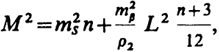(13.7)

где т_s и m_β - соответственно ошибки линейных и угловых измерений; п - число сторон в ходе; L - длина хода.

Если из общих расчетов для данной ступени получена ошибка (например, m₂) пункта в середине (слабом месте) уравненного полигонометрического хода, то ошибка в конце хода будет вдвое больше. Далее, принимая принцип равных влияний ошибок угловых и линейных измерений, из выражения (13.7) для конкретной схемы хода можно найти m_s и т_β.

Аналогичные расчеты могут быть выполнены для любого вида построения инженерно-геодезических сетей.

Принципы проектирования и расчета точности высотных сетей те же, что и для плановых. Однако следует иметь в виду, что если в качестве единицы веса μ принимается ошибка на 1 км нивелирного хода, то обратный вес в секциях следует принять равным длине секции (в км); если μ - ошибка определения превышения на станции, то обратный вес в секциях равен числу станций.

Исходная точность в зависимости от назначения высотной сети может определяться требованиями к точности рисовки рельефа на топопланах, к высотной разбивке, к точности определения осадок и т. п.

144