Форма Земли. Мысль о том, что Земля имеет форму шара, впервые высказал в VI. в. до н. э. древнегреческий ученый Пифагор, а доказал это и определил радиус Земли египетский математик и географ Эратосфен, живший в III в. до н. э. Впоследствии ученые уточнили, что Земля сплюснута у полюсов. Такая фигура в математике называется эллипсоидом вращения, она получается от вращения эллипса вокруг малой оси. В земном эллипсоиде (рис. 1.1, а) полярная ось меньше экваториальной.
Земля не является правильным геометрическим телом - ее поверхность представляет собой сочетание возвышенностей и углублений. Большая часть углублений заполнена водой океанов и морей- из 510 млн. км2 общей площади поверхности Земли 71% занимает океан. Поверхность воды в нем под действием силы тяжести образует уровенную поверхность, перпендикулярную в каждой
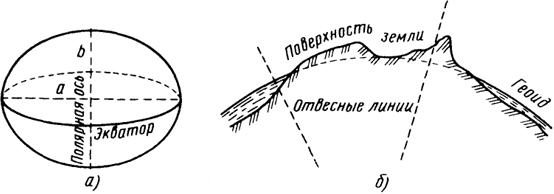
Рис. 1.1. Земной эллипсоид (
а) и геоид (
б)
6
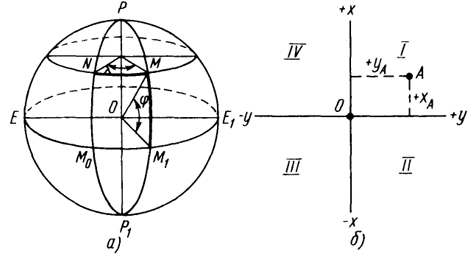
Рис. 1.2. Системы географических (
а) и плоских прямоугольных (
б) координат
точке направлению силы тяжести. Линию, совпадающую с направлением силы тяжести, называют отвесной линией. Если уровенную поверхность мысленно продолжить под материками, образуется фигура, называемая геоидом (рис. 1, б). Казалось бы, геоид наилучшим образом определяет математическую фигуру Земли, так как в каждой точке его поверхности существует одно вполне определенное направление - отвесная линия, составляющая с касательной плоскостью прямой угол. Однако из-за неравномерного распределения масс внутри Земли поверхность геоида имеет сложную форму. Поэтому за математическую фигуру для Земли принимают эллипсоид вращения, наиболее приближенный к геоиду. Земной эллипсоид соответствующим образом мысленно располагают (ориентируют) в теле Земли.
Земной эллипсоид с определенными размерами и ориентированный определенным образом для части Земли, называют референц-эллипсоидом. В нашей стране размеры референц-эллипсоида были получены под руководством выдающегося геодезиста Ф. Н. Красовского. Эти размеры утверждены для использования в работах по высшей геодезии и картографии. Референц-эллипсоиду присвоено имя Красовского. Размеры референц-эллипсоида Красовского: большая полуось а = 6378245 м, малая полуось b = 6356863 м, полярное сжатие α = а-b/a = 1/298,3.
В инженерной геодезии и работах по топографии условно считают, что Земля имеет форму шара, объем которого равен объему земного эллипсоида, радиус шара R = 6371,11 км.
Определение местоположения точек. Чтобы определить положение точек на земной поверхности, на ней условно проводят линии - параллели и меридианы, которые образуют систему географических координат (рис. 1.2, а).
Меридиан - воображаемая линия, образованная секущей плоскостью, проходящей через ось РР1 вращения Земли.
7
Параллель - воображаемая линия, образованная на поверхности Земли секущей плоскостью, перпендикулярной оси вращения Земли. Параллель, образованная плоскостью, проходящей через центр Земли,- экватор.
Один из меридианов, например меридиан PNM0P1 принимают за начальный. Тогда положение меридиана точки М определяется двугранным углом между меридианной плоскостью, проходящей через эту точку, и плоскостью начального меридиана. Этот угол называют долготой данной точки и обозначают буквой λ; Положение параллели точки М определяется углом между радиусом ОМ земного шара и плоскостью экватора. Этот угол называют широтой данной точки и обозначают буквой φ Долготу точки М можно измерить также дугой NM параллели, а широту той же точки - дугой M1M меридиана. Долгота λ и широта φ называются географическими координатами данной точки.
Начальным меридианом на поверхности Земли принято считать меридиан, проходящий через центр меридианного зала старейшей в Европе астрономической обсерватории в Гринвиче, вблизи Лондона. Долготы отсчитывают к востоку и западу от начального меридиана в пределах 0...180° и обозначают, например, так: 62° в.д. (восточной долготы) или 124° з.д. (западной долготы) от Гринвича; широты - 0...90° к северу и югу от экватора, например 56° с.ш. (северной широты) или ю.ш. (южной широты).
Положение любой точки на поверхности Земли можно определить с помощью астрономических наблюдений (астрономические координаты), вычислить по результатам геодезических измерений на местности или по наблюдению спутников (геодезические координаты).
Если геодезические работы ведут на небольшом участке, что позволяет не принимать во внимание сферичность поверхности Земли, для определения положения точки используют систему плоских прямоугольных координат (рис. 1.2, б). Систему образуют две взаимно перпендикулярные линии (оси), лежащие в горизонтальной плоскости, причем ось абсцисс х, как правило, совмещают с меридианом какой-либо точки. Точка О - начало координат. Положительное направление оси х - на север от экватора, оси у - на восток от меридиана. Оси абсцисс и ординат образуют координатные четверти I...IV, которые нумеруют по ходу часовой стрелки; северо-восточная четверть считается первой.
Например, положение точки А определяется координатами xAyA В зависимости от четверти, в которой расположена точка, перед координатами ставят знак "+" или "-".
Для полной характеристики положения точки на поверхности Земли необходимо знать еще третью координату - высоту. Высотой точки называется расстояние по отвесному направлению от
8
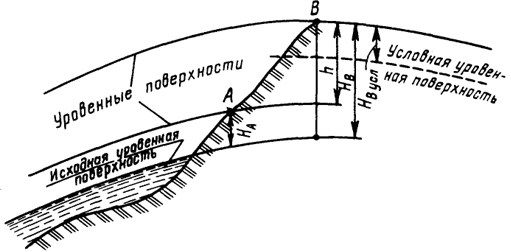
Рис. 1.3. Абсолютные, условные и относительные высоты
этой точки до уровенной поверхности. Числовое значение высоты точки называется ее отметкой.
Высоты (рис. 1.3) бывают абсолютные, условные и относительные. Абсолютные высоты, например НA, НВ, отсчитывают от исходной уровенной поверхности - среднего уровня океана или моря (в России - это нуль Кронштадтского футштока - горизонтальная черта на медной пластине, прикрепленной к устою моста через обводной канал в г. Кронштадте). Условной высотой, например HBусл, называется отвесное расстояние от точки земной поверхности до условной уровенной поверхности - любой точки, принятой за исходную (нулевую).
Относительной высотой, или превышением h точки называется высота ее над другой точкой земной поверхности (например, точки В над точкой А).
9
