5.6. НЕРАВНОТОЧНЫЕ ИЗМЕРЕНИЯ

Неравноточными называют такие измерения l₁;, l₂;, l₃;, ..., l_n;, которые выполнены соответственно с разными средними квадратическими ошибками m₁, m₂, m₃, m_n за счет разного количества приемов, использования приборов различной точности, разных условий и т. п.

Для определения в этом случае в качестве общего результата арифметической средины пользуются формулой

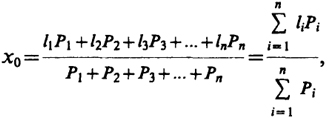(5.13)

где Р_i - вспомогательные числа, называемые весами измерений, определяющими степень доверия к их результатам. Веса вычисляют по формуле

Р_i =

μ2

m 2 i

 (5.14)

где μ - безразмерный коэффициент.

43

Понятие веса применимо и для любой функции F измеренных величин. Вес Р функции F при известной ее средней квадратической ошибке m_F вычисляют по формуле

Р_F =

μ2

m 2 F

 (5.15)

Величину μ называют "ошибкой единицы веса", так как при Р_i = 1 численно μ = m_i

Из (5.15)

m_F =

μ

√РF

  (5.16)

и

μ = m_F√Р_F(5.17)

Величину обратного веса называют обратным весом и обычно обозначают буквой q для веса измерения и Q - для веса функции.

Используя формулы (5.13) - (5.17), в практике проектирования геодезических измерений и их обработки решают две основные задачи:

• 1) установление весов неравноточных или разнородных измерений с целью совместной обработки их результатов;
• 2) определение веса функции неравноточных измерений аргументов для получения средней квадратической ошибки функции и наоборот.

Примеры подобных решений рассмотрены в главах второй части учебника.

44