В практике геодезических работ часто возникает необходимость найти среднюю квадратическую ошибку функции, если известны средние квадратические ошибки ее аргументов, и наоборот.
Рассмотрим функцию общего вида F = f(x, у, z, ...., u), где x, у, z, ..., и - независимые аргументы, полученные из наблюдений или проектного расчета со средними квадратическими ошибками тх, тy, mz, mu, ..., ти соответственно.
Из теории ошибок измерений известно, что средняя квадратическая ошибка функции независимых аргументов равна корню квадратному из суммы квадратов произведений частных производных функций по каждому из аргументов на средние квадратические ошибки соответствующих аргументов, т. е.
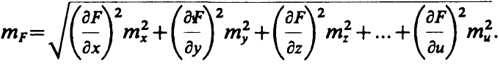 (5.7)
(5.7)
Если функция имеет вид
 (5.8)
(5.8)
то
 (5.9)
(5.9)
При mx1 = mx2 = … = mxn = mx формула (5.9) примет вид
my = mx√n.(5.10)
42
Для функции вида
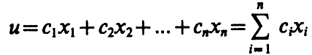 (5.11)
(5.11)
выражение для ошибок этой функции будет
 (5.12)
(5.12)
Пример. Измерены длина дачного участка а = 30,00 м со средней квадратической ошибкой 2 см и его ширина b = 20,00 м с той же средней квадратической ошибкой. Требуется найти среднюю квадратическую ошибку площади участка.
Решение.
Функция имеет вид
Р = a·b.

Так как 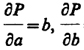 = а, та = mb = та, b то
= а, та = mb = та, b то
mP = ma, b√a2 + b2
mp = 0,02 ∙ √202 + 302 = 0,72м2.
43
