Для правильного использования результатов измерений необходимо знать, с какой точностью, т. е. с какой степенью близости к истинному значению измеряемой величины, они получены. Характеристикой точности отдельного измерения в теории ошибок служит предложенная Гауссом средняя квадратическая ошибка m, вычисляемая по формуле
 (5.2)
(5.2)
где п - число измерений данной величины.
Эта формула применима для случаев, когда известно истинное значение измеряемой величины. Такие случаи в практике встречаются редко. В то же время из измерений можно получить результат, наиболее близкий к истинному значению,- арифметическую средину. Для этого случая средняя квадратическая ошибка одного измерения подсчитывается по формуле Бесселя
 (5.3)
(5.3)
где δ - отклонения отдельных значений измеренной величины от арифметической средины, называемые вероятнейшими ошибками, причем [δ]=0.
Точность арифметической средины, естественно, будет выше точности отдельного измерения. Ее средняя квадратическая ошибка М определяется по формуле
М = m/√n(5.4)
где т - средняя квадратическая ошибка одного измерения, вычисляемая по формуле (5.2) или (5.3).
Часто в практике для контроля и повышения точности определяемую величину измеряют дважды - в прямом и обратном направлениях, например, длину линий, превышения между точками. Из двух полученных значений за окончательное принимается среднее из них. В этом случае средняя квадратическая ошибка одного измерения подсчитывается по формуле
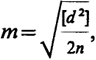 (5.5)
(5.5)
а средний результат из двух измерений - по формуле
39
 (5.6)
(5.6)
где d - разность двукратно измеренных величин, п - число разностей (двойных измерений).
В соответствии с первым свойством случайных ошибок для абсолютной величины случайной ошибки при данных условиях измерений существует допустимый предел, называемый предельной ошибкой. В строительных нормах предельная ошибка называется допускаемым отклонением.
Теорией ошибок измерений доказывается, что абсолютное большинство случайных ошибок (68,3%) данного ряда измерений находится в интервале от 0 до ±m; и интервал от 0 до ±2т попадает 95,4%, а от 0 до ± 3т - 99,7% ошибок. Таким образом, из 100 ошибок данного ряда измерений лишь пять могут оказаться больше или равны 2/71, а из 1000 ошибок только три будут больше или равны 3т. На основании этого в качестве предельной ошибки ∆пред для данного ряда измерений принимается утроенная средняя квадратическая ошибка, т. е. ∆пред = 3т. На практике во многих работах для повышения требований точности измерений принимают ∆пред = 2т. Погрешность измерений, величины которых превосходят ∆пред, считают грубыми.
Иногда о точности измерений судят не по абсолютной величине средней квадратической или предельной ошибки, а по величине относительной ошибки.
Относительной ошибкой называется отношение абсолютной погрешности к значению самой измеренной величины. Относительная ошибка выражается в виде простой дроби, числитель которой - единица, а знаменатель - число, округленное до двух-трех значащих цифр с нулями. Например, относительная средняя квадратическая ошибка измерения линии длиной l = 110 м при ml = 2 см равна ml/l = 1/5500, а относительная предельная ошибка при ∆пред = 3m∆пред/l = 1/1800.
40
