4.3. РЕШЕНИЕ ЗАДАЧ ПО КАРТАМ И ПЛАНАМ С ГОРИЗОНТАЛЯМИ

Определение крутизны ската. Крутизна ската характеризуется углом наклона v, который образует линия местности, например АВ, с горизонтальной плоскостью Р (рис. 4.6).

Из прямоугольного треугольника ABB’ следует:

tgν = h/α, (4.1)

где h - высота сечения рельефа, α - заложение.

Зная тангенс, по таблицам значений тригонометрических функций находят значение угла наклона.

Крутизну ската характеризуют также уклоном i

i = tgα. (4.2)

Уклон линии выражается в процентах или промилле (‰), т. е. тысячных долях единицы.

Как правило, при работе с картой или планом угол наклона либо уклон ската определяют, пользуясь графиками (рис. 4.7, а, б), называемыми масштабами (или шкалами) заложений.

Для этого с плана раствором циркуля берут заложение между двумя горизонталями по данному скату, затем по графику находят то место, где расстояние между кривой и горизонтальной прямой равно этому заложению. Для найденной таким образом ординаты

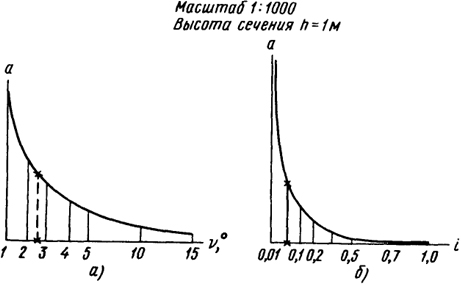
Рис. 4.7. Графики заложений к плану масштаба 1:1000 при высоте сечения рельефаh = 1 м:
а - для углов наклона, б - уклонов

33

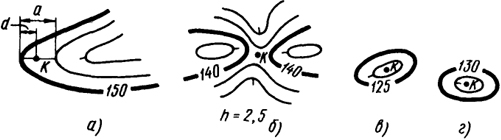
Рис. 4.8. Схемы а...г для определения отметок точек по горизонталям

прочитывают значение ν или i по горизонтальной прямой (на приведенных графиках отмечено звездочками: ν = 2,9°, i = 0,05 = 5%).

Определение отметок точек местности. Если точка расположена на горизонтали, ее отметка равна отметке горизонтали. Когда точка находится между горизонталями с разными высотами, ее отметка определяется интерполированием (нахождением промежуточных значении величин) на глаз между отметками этих горизонталей.

Интерполирование заключается в определении коэффициента пропорциональности расстояния d от определяемой точки до меньшей по значению горизонтали к величине заложения а, т. е. отношения d/a, и умножения его на значение высоты сечения рельефа h.

Пример. Отметка hk (рис. 4.8, а) точки К, расположенной между горизонталями с отметками 150 м и 152,5 м, равна H_K = H_М.Г. + (d/a)h = 150 м + 0,4 + 0,25 = 151 м.

Если определяемая точка расположена между одноименными горизонталями - на седловине (рис. 4.8, б) или внутри замкнутой горизонтали на холме или котловине (рис, 27, в, г), ее отметку можно определить лишь приближенно, считая, что ее отметка больше или меньше высоты этой горизонтали на 0,5h. Например, на рисунке для седловины отметка точки К равна 138,8, для холма - 128,8 м, для котловины - 126,2 м.

Проведение на карте линии заданного предельного уклона (рис. 4.9). Между заданными на карте точками А и В требуется провести кратчайшую линию так, чтобы ни один отрезок не имел уклона больше заданного предельного i_пред.

Проще всего задача решается с помощью масштаба заложения для уклонов. Взяв по нему раствором циркуля заложение a_пред, соответствующее предельному уклону, засекают последовательно точки 1...7 - все горизонтали от точки А до точки В. Если раствор циркуля меньше расстояния между горизонталями, линию проводят по кратчайшему направлению. Соединив все точки, получают линию с заданным предельным уклоном.

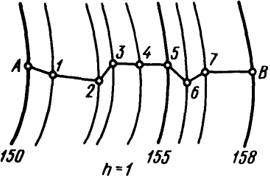
Рис. 4.9. Схема проведения на карте линии заданного предельного уклона

34

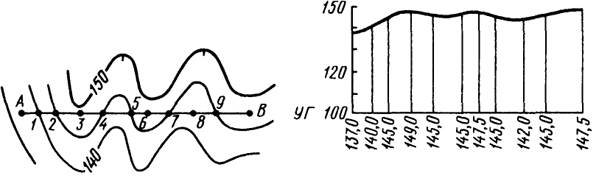
Рис. 4.10. Схемы построения профиля по заданному направлению

Если нет масштаба заложений, заложение а_пред можно подсчитать по формуле a_пред = h/(i_предM, где М - знаменатель числового масштаба карты.

Построение профиля местности по заданному на карте направлению. Рассмотрим построение профиля на конкретном примере (рис. 4.10). Пусть требуется построить профиль местности по линии АВ. Для этого линию АВ переносят в масштабе карты на бумагу и отмечают на ней точки 1, 2, 4, 5, 7, 9, в которых она пересекает горизонтали, а также характерные точки рельефа (3, 6, 8). Линия АВ служит основанием профиля. Взятые с карты отметки точек откладывают на перпендикулярах (ординатах) к основанию профиля в масштабе, в 10 раз превышающем горизонтальный масштаб. Полученные точки соединяют плавной линией. Обычно ординаты профиля уменьшают на одну и ту же величину, т. е. строят профиль не от нуля высот, а от условного горизонта УГ (на рис. 29 за условный горизонт принята высота, равная 100 м).

С помощью профиля можно установить взаимную видимость между двумя точками, для чего их нужно соединить прямой линией. Если построить профили из одной точки по нескольким направлениям, можно нанести на карту или план участки местности, не видимые с этой точки. Такие участки называют полями невидимости.

Вычисление объемов (рис. 4.11). По карте с горизонталями можно вычислить объемы горы и котловины, изображаемых системой горизонталей, замыкающихся в пределах небольшой площадки. Для этого формы рельефа делят на части, ограниченные двумя соседними горизонталями.

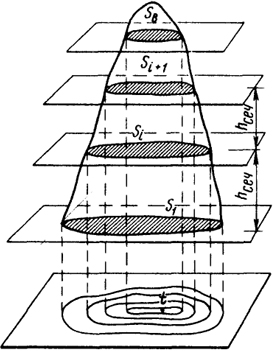
Рис. 4.11. Схема определения объема по карте с горизонталями

35

Каждую такую часть можно приближенно принять за усеченный конус, объем которого равен V_i = (1/2)(S_i + S_i+j)h_сеч, где S_i и S_i+1 - площади, ограниченные на карте нижней и верхней горизонталями, являющимися основаниями усеченного конуса, h_сеч - высота сечения рельефа, i = 1, 2, ..., k - текущий номер усеченного конуса.

Площади S измеряют планиметром (механическим или электронным).

Приближенно площадь участка можно определить, деля его на ряд правильных математических фигур (трапеций, треугольников и т. п.) и суммируя по площади. Объем V_B самой верхней части вычисляют как объем конуса, площадь основания которого равна S_B а высота h - разности отметок верхней точки t и горизонтали, ограничивающей основание конуса: V_B = (S_B/3)h.

Если отметка точки t на карте не подписана, то принимают h = h_сеч/2.

Полный объем вычисляют как сумму объемов отдельных частей: V = V₁ + V₂ + ... + V_k + V_B, где k - число частей.

36