Для вынесения проекта тоннеля в натуру необходимо знать координаты всех пикетов трассы и точек кривых.
На прямых участках приращения координат между пикетами вычисляют по известным формулам
∆xi = dcosαi; ∆yi = dsinαi,(27.4)
где d - проектное расстояние между пикетами, обычно равное 100000 мм; αi - дирекционный угол прямых участков, определяемый через углы поворота трассы
αi+1 = αi + θп = αi - θл,(27.5)
где θп и θл - соответственно углы поворота трассы вправо и влево.
Координаты пикетов, расположенных на круговой кривой, можно вычислить или через центральные углы и длины радиусов от координат центра кривой, или по стягивающим хордам и углам между ними.
Центральные углы определяют по формулам
γ1 =
ρ; γП =
ρ; γНП =
ρ; γ2 =
ρ,(27.6)
где γ1 - центральный угол (рис. 27.5) при точке О между радиусами, проведенными через точку НКК и первый пикет, лежащий на кривой; γ2 - центральный угол между радиусами, проведенными через последний пикет, лежащий на кривой, и точку ККК; γП - центральный угол, соответствующий нормальному пикету; γНП - центральный угол, соответствующий неправильному пикету;
413
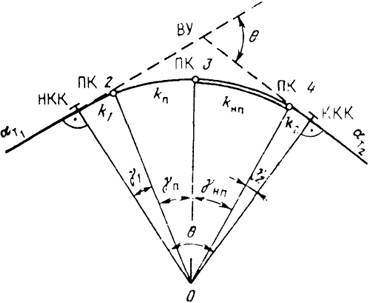
Рис. 27.5. Схема определения координат пикетов на кривой по радиусам и центральным углам
k1, k2, kП и kНП дуг, соответствующие центральным углам γ1 γ2, γП, γНП.
Вычисленные значения центральных углов проверяют по формуле:
γ1 + nγП + γНП + γ2 = θ,(27.7)
где n - число нормальных пикетов; θ - угол поворота трассы.
Аналогичному равенству должны удовлетворять длины круговых кривых, используемых для вычисления центральных углов, т. е.
k1 + nkП + kНП + k2 = K,(27.8)
где К - длина всей круговой кривой.
Координаты центра кривой от точек начала круговой кривой вычисляют по формулам
хO = xНКК + Rcos(αT1 + 90°); yO = yНКК + Rsin(αT1 + 90°),(27.9)
где (αT1 - дирекционный угол первого тангенса. Дирекционные углы направлений на пикеты кривой из центра О определяют от известного дирекционного угла линии О - НКК, равного (αT1), путем прибавления соответствующего центрального угла γ. По этим дирекционным углам и принятому радиусу находят приращения координат относительно центра кривой
∆xi = Rcos(αT1 + 270° + γi); ∆yi = Rsin(αT1 + 270° + γi).(27.10)
Для вычисления координат по стягивающим хордам кривой необходимо знать дирекционные углы и длины этих хорд.
Дирекционные углы хорд определяют от исходных дирекционных углов линий тангенсов αT1 и αT2 по значениям углов поворота хорд, вычисляемых из равнобедренных треугольников, которые образованы радиусами и стягивающими хордами. Например, для приведенной схемы расчета (см. рис. 27.5) получим:
414
| Точки |
углы поворота |
| НКК |
180° -
|
| ПК2 |
180° -
-
|
| ПК3 |
180° -
-
|
| ПК4 |
180° -
-
. |
| ККК |
180° -
|
Длины хорд bi, определяют из равнобедренных треугольников по значениям кривых ki и центральных углов γi (рис. 27.6):
= Rsin
.(27.11)
Следовательно,
bi = 2Rsin
.(27.12)
Контроль вычислений длин хорд может быть проведен по формуле
bi = ki -
.(27.13)
Для дальнейших вычислений необходимо получить координаты точек начал переходных кривых (НПК). Исходными данными для этого расчета служат координаты начала (НКК) и конца круговой кривой (ККК), а также дирекционные углы прямых участков трассы, примыкающих к круговой кривой (рис. 27.7).
Расстояние между началом переходной кривой и началом или концом круговой кривой определяют по следующей формуле:
t1 =
+
.(27.14)
Для контроля вычисляют и значение t2:
t2 =
+ (27.15)
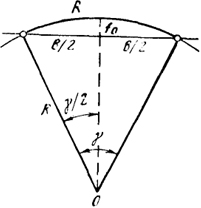
Рис. 27.6. Схема определения длин хорд на кривой
415
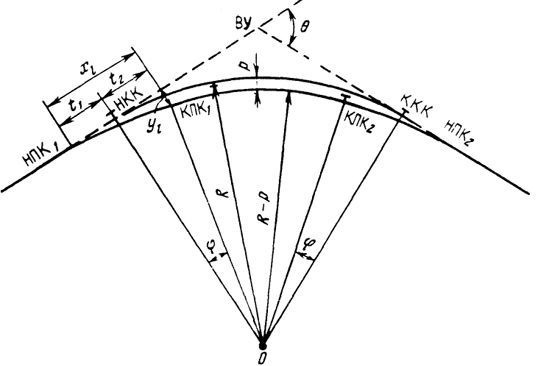
Рис. 27.7. Схема смещения оси пути за счет вставки переходных кривых
Величины l и с берут с проектного чертежа. Координаты концов переходных кривых вычисляют двумя способами: через центральный угол φ или через абсциссу xl и ординату yl.
Угол поворота φ переходной кривой вычисляют по формуле
φ =
ρ.(27.16)
Расстояние между центром О круговой кривой и концом переходной кривой является радиусом оси пути, т. е. Rпут = R - p, где смещение р вычисляется по формуле (27.1).
При вычислении координат концов переходных кривых через угол φ за исходные принимают координаты начала (НКК) и конца круговой кривой (ККК), а также дирекционные углы радиусов, соединяющих эти точки с центром круговой кривой.
При вычислении координат конца переходной кривой по абсциссе xl и ординате yl за начало координат принимают точку начала переходной кривой (НПК), а за ось x - линию тангенсов.
Величины хl и yl вычисляют по формулам
xl = l -
; yl =
.(27.17)
Контролем вычисления значений xl служит выражение: t1 + t2 = xl.
Координаты концов переходных кривых и пикетов вычисляют
как на оси пути, так и на оси тоннеля, при этом величины радиусов
416
соответственно должны быть равны Rпут = R - p, Rт = R - (p + q), где Rпут - радиус круговой кривой на оси пути; Rт - то же, на оси тоннеля; р и q - смещения осей, вычисленные по формулам (27.1) и (27.2).
Перенесение в натуру оси тоннеля на круговых кривых выполняют по ломаному контуру, состоящему из прямых линий, находящихся под некоторым углом друг к другу. В качестве прямых линий выбирают или хорды, или секущие. Чем больше длины хорд или секущих, тем меньшее их число уложится на разбиваемой в натуре кривой. Однако при этом увеличивается стрелка прогиба/), которая для хорды вычисляется по формуле
f0 =
,(27.18)
где kb - длина круговой кривой, стягиваемая хордой b.
В то же время, уменьшение числа хорд или секущих приводит к сокращению объема разбивочных работ.
На практике для уменьшения объема разбивочных работ круговые кривые целесообразно переносить в натуру на оси тоннеля и на оси пути по секущим. Поэтому рассмотрим метод определения координат концов хорд на оси тоннеля.
Из формулы (27.18) можно определить длину кривой, стягиваемой хордой, при которой стрелка прогиба не превышает величины kb = √8Rfmax. Для вычисления приближенной длины хорды b’ можно принять ее длину равной длине опирающейся на нее кривой, тогда
b’ = √8Rfmax.(27.19)
При выносе в натуру круговой кривой по хордам необходимо вычислить координаты концов хорд. Это можно сделать двумя путями: равными хордами, так чтобы в пределах разбиваемой кривой они имели одинаковую длину с точностью до 1 мм, или хордами, длины которых выражены целым числом метров с последней хордой (остатком), имеющей длину, вычисленную до 1 мм.
При условии равенства длин хорд в пределах круговой кривой на оси тоннеля (между концами переходных кривых) определяют приближенную их длину. Затем, пользуясь приближенной длиной хорды, подсчитывают их приближенное число n’ = Kт/b’. Длина кривой на оси тоннеля выражается формулой
Kт =
,(27.20)
где θт = θ - 2φ; Rт = R - (p + q).
Далее устанавливают целое число хорд. Чтобы максимальное значение стрелки прогиба не превышало принятой величины, которая
417
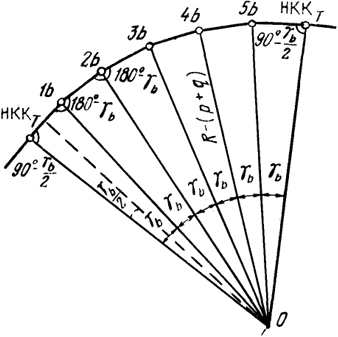
Рис. 27.8. Схема разбивки оси тоннеля на кривой по хордам
чаще всего характеризуется величиной габаритного запаса (для тоннелей на путях сообщения принимается равным 100 мм), полученное значение п' округляют до ближайшего целого числа.
Затем вычисляют длину кривой, соответствующую длине принятой хорды, по формуле kb =
. Зная длину кривой
kb, вычисляют центральные углы γ
b и длину стягивающей хорды
b по формулам
γb =
ρ; b = 2Rтsin (
).(27.21)
Координаты концов хорд находят по замкнутому ходу, состоящему из хорд и радиусов Rт, которые соединяют центр кривой О и концы переходных кривых, расположенных на оси тоннеля (рис. 27.8). При этом угол поворота между радиусом и первой хордой, а также угол поворота между последней хордой и радиусом равны (90° -
). Тогда углы поворота, обращенные к центру кривой, между последующими хордами равны 180° - γ
b.
418
