Определение площадей земельных участков является одним из важнейших видов геодезических работ для целей земельного кадастра.
В зависимости от хозяйственной значимости земельных участков, наличия планово-топографического материала, топографических условий местности и требуемой точности применяют различные способы определения площадей.
1. Аналитический, когда площадь вычисляется по результатам измерений линий на местности, по результатам измерений линий и углов на местности или по их функциям (координатам вершин фигур).
2. Графический, когда площадь вычисляется по результатам измерений линий или координат на плане (карте).
3. Механический, когда площадь определяется по плану с помощью специальных приборов (планиметров) или приспособлений (палеток). Иногда эти способы применяют комбинированно, например, часть линейных величин для вычисления площади определяют по плану, а часть берут из результатов измерений на местности.
Площади можно также определить на ЭВМ по цифровой модели местности по специальной программе.
При аналитическом способе определения площадей применяются формулы геометрии, тригонометрии и аналитической геометрии. При определении площадей небольших участков (для учета площадей, занятых строениями, усадьбами, площадей вспашки, посева) участки разбиваются на простейшие геометрические фигуры, преимущественно треугольники, прямоугольники, реже трапеции. В этом случае площади участков определяются как суммы площадей отдельных фигур, вычисляемых по линейным элементам - высотам и основаниям.
335
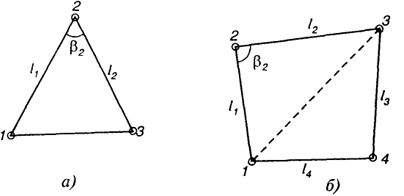
Рис. 23.1. Геометрические фигуры для определения площадей участков (
а, б)
Если по границам участка выполнены геодезические измерения, то площадь всего участка или его части можно вычислить по формулам, приведенным применительно к следующим фигурам участков (рис. 23.1).
Треугольник (рис. 23.1, а). Площадь треугольника определяется по сторонам l1 и l2, углу β2, заключенному между ними, по формуле
P =
(l1·l2·sinβ2).(23.1)
Четырехугольник (рис. 23.1, б). В зависимости от элементов, известных в четырехугольнике, могут быть использованы различные формулы для расчета, в связи с чем приведем пример, характеризующий это многообразие. Пусть в четырехугольнике измерены все стороны и один угол при вершине 2. В таком случае площадь треугольника 1 - 2 - 3 может быть вычислена по формуле (23.1). При этом полезно вычислить длину l1-3, используя теорему косинусов
l1-3 = √
+ l2 -2·l1·l2·cosβ.(23.2)
Площадь треугольника 1 - 3 - 4 может быть вычислена по формуле
P = √S·(S - l3)·(S - l4)·(S - l1-3),(23.3)
где S - полупериметр, равный
S =
(
l3 +
l4 +
l1-3).
Общая площадь четырехугольника будет равна:
P =
·sinβ2 + √S·(S - l3)·(S - l4)·(S - l1-3).(23.4)
При наличии координат вершин полигона площади треугольника и четырехугольника удобно вычислять соответственно по формулам:
336
P =
·[(X1 - X2)·(Y2 - Y3) - (Y1 - Y2)·(X2 - X3)],(23.5)
P =
·[(X1 - X3)·(Y2 - Y4) - (Y1 - Y3)·(X2 - X4)],(23.6)
Если полигон имеет более четырех углов, то площадь его быстрее и с хорошим контролем можно получить по координатам Хi и Yi его вершин или по приращениям координат ∆Xi и ∆Yi после увязки полигона, например, по формулам
 (23.7)
(23.7)
или
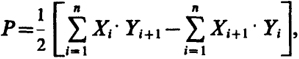 (23.8)
(23.8)
 (23.9)
(23.9)
или
 (23.10)
(23.10)
Координаты вершин полигона для определения площади участка как в государственной так и в местной системах могут быть получены любым из известных геодезических способов: триангуляционными или линейно-угловыми построениями; проложенном полигонометрических или теодолитных ходов; угловыми, линейными и полярными засечками; спутниковыми приемниками для определения местоположения и т. д.
Кроме того, когда требуется определить только площадь или границы участка в его частной системе координат, можно применять так называемый способ изолированных базисов. Суть его заключается в том, что координаты точек объекта определяют засечками с изолированных друг от друга базисов, расположенных в удобных местах вблизи (рис. 23.2, а) или внутри (рис. 23.2, б) участка. Для приведения результатов измерений в одну систему координат необходимо, чтобы было выполнено условие перекрытия, т. е. со смежных базисов должен быть определен ряд (минимум две) общих точек.
337
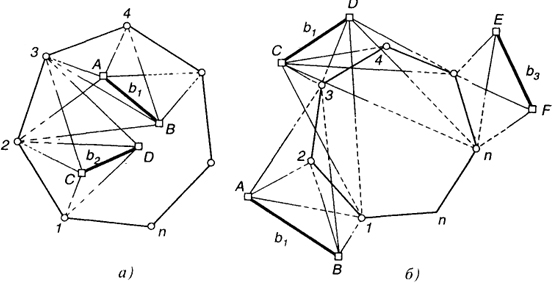
Рис. 23.2. Определение координат точек участка с изолированных базисов (
а, б)
Для каждой из п общих точек смежных базисов, например b1 и b2, можно записать два уравнения связи вида
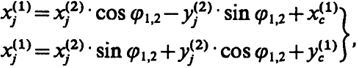 (23.11)
(23.11)
из которых по методу наименьших координат определяется угол φ1,2 разворота систем координат и координаты x
и
y
начала координат системы 2 в системе 1. Установив параметры преобразования координат, в правые части этих формул подставляют координаты
x
и
y
остальных (
m-n) точек, определенных со второго базиса, переводя их тем самым в первую систему. Аналогичным образом решается задача для всех точек, определяемых с базисов
b3,
b4, и т. д.
При графическом способе определения площадей участок на плане разбивают на простейшие геометрические фигуры.
При разбивке участка на простейшие фигуры можно принять много вариантов, однако точность вычисления площади участка при различных вариантах не будет одинаковой. Площадь треугольника графическим способом вычисляется точнее площадей, определяемых разбивкой на прямоугольники, трапеции и другие фигуры. Механический способ определения площадей наиболее целесообразно применять для участков с ломаными линиями. Можно определить площади прямолинейными и криволинейными палетками.
При определении площадей по плану графическим или механическим способом (с помощью планиметра и палеток) необходимо учитывать деформацию бумаги (плана). Величина деформации может характеризоваться коэффициентом q, определяемым в двух взаимно перпендикулярных направлениях, по формуле:
338
q =
,(23.12)
где L0 - теоретическая длина линии, значащаяся на плане (например, длина стороны квадрата координатной сетки); L - результат измерения этой линии по плану.
В настоящее время механические планиметры заменили электронные (цифровые). Представляют интерес цифровые планиметры, выпускаемые фирмой "Торсоп", которая предлагает несколько моделей цифровых планиметров, позволяющих проводить измерения площадей по картам или другим материалам с точностью ±0,2%.
Если для определения площадей используются пункты государственной геодезической сети, то полученные площади чаще всего имеют несколько преуменьшенное значение, потому что координаты пунктов относятся не к поверхности Земли, а к поверхности принятого референс-эллипсоида. На больших высотах этой разницей не всегда можно пренебречь.
Переход от площади Р0 на поверхности референс-эллипсоида к площади Р на поверхности Земли на высоте Н может быть выполнен по формуле
P = P0(1 +
),(23.13)
где R - радиус Земли, равный 6370 км.
Пользуясь координатами пунктов, планами (картами) в проекции Гаусса-Крюгера площади участков и размеры получаются всегда больше их горизонтальных проекций, и это увеличение возрастает по мере удаления от осевого меридиана зоны. Для приведения площади к горизонтальной проекции используют формулу
P = Pпр[1 - (
)],(23.14)
где Ym - средняя ордината участка (расстояние от осевого меридиана зоны до середины участка).
Кстати, приведенный выше способ изолированных базисов свободен от поправок за переход от поверхности референц-эллипсоида и проекции Гаусса-Крюгера, так как координаты точек базисов и границ участков определяются в частной системе на физической поверхности Земли.
Иногда возникает необходимость получения площадей физической (топографической) поверхности участка Рф, которая тем больше отличается от площади горизонтального проложения участка Ргп, чем больше угол наклона ν или уклон i местности. Для получения площади физической поверхности участка его разбивают
339
на части с одинаковыми скатами, т. е. с равностоящими, и более или менее прямыми горизонталями. На каждой из этих частей в перпендикулярном направлении к горизонталям определяют угол наклона или уклон и вычисляют площадь Рф на физической поверхности земли по формулам
Pф = Pгп(1 +
),(23.15)
Pф = Pгп(1 +
).(23.16)
Например, уже при угле наклона ν = 2,9° (уклоне i = 0,05) поправка составит 1:800, или 12,5 м2 на 1 га.
Требования к точности определения площади земельных участков зависят от многих факторов: хозяйственной значимости (сельхозугодья, лесные угодья, городская территория и т. п.); местоположения (центр города, его окраина и т. п.); экологической обстановки (химическая загрязненность земли, атмосферы и т. п.); наличия и ценности недвижимости. Все эти и другие возможные факторы влияют на нормативную стоимость земли, которая в основном и является исходной для расчета требуемой точности определения площади земельных участков.
Достижение требуемой точности возможно лишь при правильном выборе способа определения площади участка. Очевидно, что наивысшая точность может быть достигнута при аналитическом способе определения площади. В этоме способе площадь участка определяется по результатам измерений на местности и ошибка в определении площади будет зависеть от ошибок этих измерений, так ошибку тр площади треугольника и прямоугольника, вычисляемую по измеренным высоте h с ошибкой mh и основанию l с ошибкой ml определяют по формуле
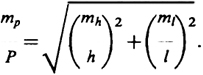 (23.17)
(23.17)
При одинаковой относительной ошибке измерения h и l
=
=
, mp =
·√2.(23.18)
Например, при Р = 1 га (10000 м2) и
=
,
тp = 7 м
2. Из выражения (23.18) для полигона с
п вершинами можно получить формулу ошибки площади вида
340
mp =
·mx.y√
D
,(23.19)
где т - средняя квадратическая ошибка определения координат х и у точек вершин полигона при условии, что
mX1 = mX2 = … mY1 = mY2 = mYn = mX,Y2,
Di - расстояние от начала координат до i-той точки вершины полигона (в частном случае от одной из вершин, принятой за начало координат).
Для прямоугольника со сторонами а и b формула (23.19) примет вид
mp =
√a2 + b2,(23.20)
а для квадрата со стороной а
тp = a·mx,y.(23.21)
Так, например, если для участка размером 100 × 100 м и площадью 1 га определять координаты со средней квадратической ошибкой 0,02 м, то ошибка площади будет равна 2 м2.
Для ошибки площади участка, определяемой по топографическому плану (карте), с учетом ошибок измерений на местности и ошибок составления топоплана можно использовать формулу вида
(mp)м2 =
√(P)м2,(23.22)
где М - знаменатель численного масштаба плана, Р - площадь участка.
В таблице 23.1 приведены величины средних квадратических ошибок, вычисленных по формуле (23.22) для различных площадей участков по планам различных масштабов.
Таблица 23.1
| Площадь |
Масштабы |
| P |
1:500 |
1:1000 |
1:2000 |
| (кв. м) |
т (кв. м) |
т (кв. м) |
т (кв. м) |
| 400 |
3,0 |
6,0 |
12,0 |
| 600 |
3,6 |
7,3 |
14,6 |
| 1200 |
16,4 |
32,8 |
65,6 |
| 2500 |
23,7 |
47,4 |
94,8 |
| 10000 |
47,4 |
94,8 |
189,6 |
341
Приведенные формулы являются приближенными, так как не учитывают возможных ошибок исходных данных и зависимости между входящими в них величинами. Однако они вполне достаточны для предварительных (проектных) расчетов.
342
