Бетон рассматривается как иерархическая система, на мезуровне - двухфазный материал, в котором зерна заполнителя включены в цементную матрицу. Вяжущим элементом этой системы являются микротрещины
18
в интерфейсе между заполнителем и матрицей, представляющей собой трехфазовую среду.
Предложена [40] упруго-вязко-хрупкая модель бетона (рис. 1.7). Две пружины вверху моделируют твердую матрицу без трещин, а вязкий элемент - жидко-газовую среду. Параметр Esl характеризует сопротивление бетона, обусловленное скольжением краев трещин в интерфейсе; Еmc -характеризует жесткость матрицы с трещинами; Еm - аналогичный параметр для матрицы без трещин; Еm = Еm - Еc; b - коэффициент вязкости.
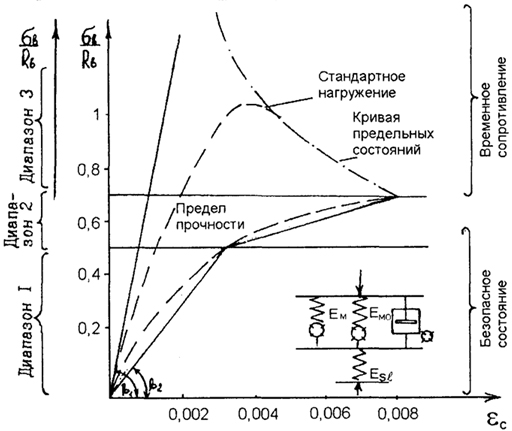Рис. 1.7. Диаграмма относительная прочность - деформация бетона а), деформирования
бетона при осевом сжатии б)
При σ = σ / σ u≈0,4...0,6 левая пружина выходит из строя, что соответствует началу распространения трещин, и происходит выдавливание воды из пор в трещины (разрушение клапана вязкого элемента). При σ≈0,75 - 0,85 вторая пружина верхнего элемента также выходит из строя и это соответствует образованию сети микротрещин в матрице, т.е. началу разрушения образца. Этот уровень рассматривается как предел прочности (рис. 1.7).
При σ≥ 0,75 - 0,85 сопротивление рассматривается как временное, обусловленное главным образом деформациями вязкого элемента. В случае быстрых нагружений жидкая фаза ведет себя как несжимаемая жидкость, блокируя деформацией верхнего элемента и оставляя возможность деформирования только нижней пружины. При этом Esl=Eb.
19
Если обозначить через Rb независимый предел прочности, то напряжения, соответствующие началу роста трещин, равны 0,67 ψ b. Для
ψ b ≤0,67Rb,Еm = КЕsl/(Еsl- К);(1.31)
0,67Rb < ψ b < Rb; Emc =KlEsl/(Esl -Кl),(1.32)
где К1 - параметр общей жесткости бетона с трещинами, получаемый из опыта как секущий модуль кривой полных деформаций нелинейной ползучести.
20
